Тангенциальная составляющая ускорения 17 страница

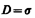(92.1)

или

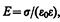(92.2)

где e — диэлектрическая проницаемость среды, окружающей проводник.

Таким образом, напряженность электростатического поля у поверхности провод­ника определяется поверхностной плотностью зарядов. Можно показать, что соот­ношение (92.2) задает напряженность электростатического поля вблизи поверхности проводника любой формы.

Если во внешнее электростатическое поле внести нейтральный проводник, то свободные заряды (электроны, ионы) будут перемещаться: положительные — по полю, отрицательные — против поля (рис. 142, а). На одном конце проводника будет скап­ливаться избыток положительного заряда, на другом — избыток отрицательного. Эти заряды называютсяиндуцированными. Процесс будет происходить до тех пор, пока напряженность поля внутри проводника не станет равной нулю, а линии напряжен­ности вне проводника — перпендикулярными его поверхности (рис. 142, б). Таким образом, нейтральный проводник, внесенный в электростатическое поле, разрывает часть линий напряженности; они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростати­ческой индукцией.

Из рис. 142, б следует, что индуцированные заряды появляются на проводнике вследствие смещения их под действием поля, т. е. s является поверхностной плот­ностью смещенных зарядов. По (92.1), электрическое смещение D вблизи проводника численно равно поверхностной плотности смещенных зарядов. Поэтому вектор D по­лучил название вектора электрического смещения.

Таккак в состоянии равновесия внутри проводника заряды отсутствуют, то созда­ние внутри него полости не повлияет на конфигурацию расположения зарядов и тем самым на электростатическое поле. Следовательно, внутри полости поле будет отсут­ствовать. Если теперь этот проводник с полостью заземлить, то потенциал во всех точках полости будет нулевым, т. е. полость полностью изолирована от влияния внешних электростатических полей. На этом основанаэлектростатическая защи­та — экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Вместо сплошного проводника для защиты может быть использована густая металлическая сетка, которая, кстати, является эффективной при наличии не только постоянных, но и переменных электрических полей.

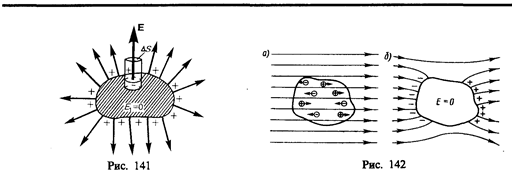
Свойство зарядов располагаться на внешней поверхности проводника используется для устройстваэлектростатических генераторов, предназначенных для накопления бо­льших зарядов и достижения разности потенциалов в несколько миллионов вольт. Электростатический генератор, изобретенный американским физиком Р. Ван-де-Граафом (1901—1967), состоит из шарообразного полого проводника 1 (рис. 143), укре­пленного на изоляторах 2. Движущаяся замкнутая лента 3 из прорезиненной ткани заряжается от источника напряжения с помощью системы остриев 4, соединенных с одним из полюсов источника, второй полюс которого заземлен. Заземленная пласти­на 5 усиливает стекание зарядов с остриев на ленту. Другая система остриев 6 снимает заряды с ленты и передает их полому шару, и они переходят на его внешнюю поверхность. Таким образом, сфере передается постепенно большой заряд и удается достичь разности потенциалов в несколько миллионов вольт. Электростатические генераторы применяются в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.

§ 93. Электрическая емкость уединенного проводника

Рассмотримуединенный проводник, т. е. проводник, который удален от других провод­ников, тел и зарядов. Его потенциал, согласно (84.5), прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряжен­ными, имеют различные потенциалы. Поэтому для уединенного проводника можно записать

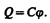
Величину

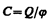(93.1)

называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изме­няет его потенциал на единицу.

Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала.

Единица электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного провод­ника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл.

Согласно (84.5), потенциал уединенного шара радиуса R, находящегося в однород­ной среде с диэлектрической проницаемостью e, равен

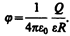
Используя формулу (93.1), получим, что емкость шара

(93.2)

Отсюда следует, что емкостью 1 Ф обладал бы уединенный шар, находящийся в ваку­уме и имеющий радиус R=C/(4pe₀)»9×10⁶км, что примерно в 1400 раз больше радиуса Земли (электроемкость Земли С»0,7 мФ). Следовательно, фарад — очень большая величина, поэтому на практике используются дольные единицы - миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ). Из формулы (93.2) вытекает также, что единица электрической постоянной e₀ — фарад на метр (Ф/м) (см. (78.3)).

§ 94. Конденсаторы

Как видно из § 93, для того чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, об­ладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили названиеконденсаторов.

Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду Q будут заряды противоположного знака. Эти заряды, естественно, ослабляют поле, создаваемое зарядом Q, т. е. понижают потенци­ал проводника, что приводит (см. (93.1)) к повышению его электроемкости.

Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми заря­дами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют (см. § 82): 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся наплоские, цилиндрические и сферические.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начина­ются на одной обкладке и кончаются на другой, поэтому свободные заряды, воз­никающие на разных обкладках, являются равными по модулю разноименными заря­дами. Подемкостью конденсатора понимается физическая величина, равная отноше­нию заряда Q, накопленного в конденсаторе, к разности потенциалов (j₁ —j₂) между его обкладками:

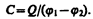(94.1)

Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. Его можно рассчитать используя формулы (86.1) и (94.1). При наличии диэлектрика между обкладками разность потенциалов между ними, согласно (86.1),

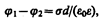(94.2)

где e — диэлектрическая проницаемость. Тогда из формулы (94.1), заменяя Q=sS, с учетом (94.2) получим выражение для емкости плоского конденсатора:

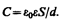(94.3)

Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиаль­ных цилиндров с радиусами r₁ и r₂ (r₂ > r₁), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Разность потенциалов между обкладками вычислим по формуле (86.3) для поля равномерно заряженного бесконечного цилиндра с линейной плотностью t =Q/l (l—длина об­кладок). При наличии диэлектрика между обкладками разность потенциалов

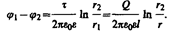(94.4)

Подставив (94.4) в (94.1), получим выражение для емкости цилиндрического конденсатора:

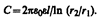(94.5)

Для определения емкости сферического конденсатора, состоящего из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу (86.2) для разности потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ (r₂ > r₁) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов

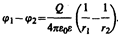(94.6)

Подставив (94.6) в (94.1), получим

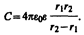
Если d=r₂—r₁<<r₁, то r₂ » r₁ » r и C=4pe₀er²/d. Так как 4pr² —площадь сферической обкладки, то получаем формулу (94.3). Таким образом, при малой величине зазора по сравнению с радиусом сферы выражения для емкости сферического а плоского конденсаторов совпадают. Этот вывод справедлив и для цилиндрического конденсатора: при малом зазоре между цилиндрами по сравнению с их радиусами в формуле (94.5) ln (r₂/r₁) можно разложить в ряд, ограничиваясь только членом первого порядка. В результате опять приходим к формуле (94.3).

Из формул (94.3), (94.5) и (94.7) вытекает, что емкость конденсаторов любой формы прямо пропорциональна диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками. Поэтому применение в качестве прослойки сегнетоэлектриков значительно увеличивает емкость конденсаторов.

Конденсаторы характеризуются пробивным напряжением — разностью потенциа­лов между обкладками конденсатора, при которой происходит пробой — электричес­кий разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины.

Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи, при этом используется их параллельное и последовательное соединения.

1. Параллельное соединение конденсаторов (рис. 144). У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна j_A – j_B. Если емкости отдельных конденсаторов С₁, С₂, ..., С_n, то, согласно (94.1), их заряды равны

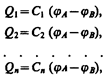
а заряд батареи конденсаторов

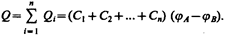
Полная емкость батареи

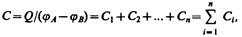
т. е. при параллельном соединении конденсаторов она равна сумме емкостей отдель­ных конденсаторов.

2. Последовательное соединение конденсаторов (рис. 145). У последовательно соеди­ненных конденсаторов заряды всех обкладок равны по модулю, а разность потенци­алов на зажимах батареи

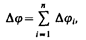
где для любого из рассматриваемых конденсаторов Dj_i = Q/С_i. С другой стороны,

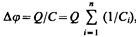
откуда

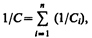
т. е. при последовательном соединении конденсаторов суммируются величины, об­ратные емкостям. Таким образом, при .последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в ба­тарее.

§ 95. Энергия системы зарядов, уединенного проводника и конденсатора. Энергия электростатического поля

1. Энергия системы неподвижных точечных зарядов. Электростатические силы взаимо­действия консервативны (см. § 83); следовательно, система зарядов обладает потенци­альной энергией. Найдем потенциальную энергию системы двух неподвижных точеч­ных зарядов Q₁и Q₂, находящихся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (см. (84.2) и (84.5)):

где j₁₂ и j₂₁ — соответственно потенциалы, создаваемые зарядом Q₂ в точке нахожде­ния заряда Q₁ и зарядом Q₁ в точке нахождения заряда Q₂. Согласно (84.5),

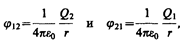
поэтому W₁ = W₂ = W и

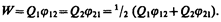
Добавляя к системе из двух зарядов последовательно зарядыQ₃, Q₄, ... , можно убедиться в том, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна

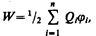(95.1)

где j_i — потенциал, создаваемый в той точке, где находится заряд Q_i, всеми зарядами, кроме i-го.

2. Энергия заряженного уединенного проводника. Пусть имеется уединенный провод­ник, заряд, емкость и потенциал которого соответственно равны Q, С, j. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконеч­ности на уединенный проводник, затратив на это работу, равную

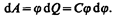
Чтобы зарядить тело от нулевого потенциала до j, необходимо совершить работу

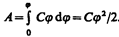(95.2)

Энергия заряженного проводника равна той работе, которую необходимо совер­шить, чтобы зарядить этот проводник:

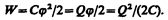(95.3)

Формулу (95.3) можно получить и из того, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Пола­гая потенциал проводника равным j, из (95.1) найдем

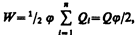
где 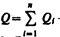- заряд проводника.

3. Энергия заряженного конденсатора. Как всякий заряженный проводник, конден­сатор обладает энергией, которая в соответствии с формулой (95.3) равна

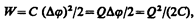(95.4)

где Q — заряд конденсатора, С — его емкость, Dj — разность потенциалов между обкладками конденсатора.

Используя выражение (95.4), можно найтимеханическую (пондеромоторную) силу, с которой пластины конденсатора притягивают друг друга. Для этого предположим, что расстояние х между пластинами меняется, например, на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx = — dW, откуда

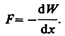(95.5)

Подставив в (95.4) выражение (94.3), получим

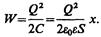(95.6)

Производя дифференцирование при конкретном значении энергии (см. (95.5) и (95.6)), найдем искомую силу:

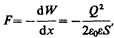
где знак минус указывает, что сила F является силой притяжения.

4. Энергия электростатического поля. Преобразуем формулу (95.4), выражающую энергию плоского конденсатора посредством зарядов и потенциалов, воспользовав­шись выражением для емкости плоского конденсатора (C=e₀eS/d) и разности потенци­алов между его обкладками (Dj=Ed. Тогда

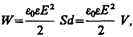(95.7)

где V= Sd — объем конденсатора. Формула (95.7) показывает, что энергия конден­сатора выражается через величину, характеризующую электростатическое поле, — на­пряженность Е.

Объемная плотность энергии электростатического поля (энергия единицы объема)

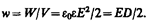(95.8)

Выражение (95.8) справедливо только дляизотропного диэлектрика, для которого выполняется соотношение (88.2):Р ={e₀Е.

Формулы (95.4) и (95.7) соответственно связывают энергию конденсатора с зарядом на его обкладках и с напряженностью поля. Возникает, естественно, вопрос о локализа­ции электростатической энергии и что является ее носителем — заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика изучает постоянные во времени поля неподвижных зарядов, т. е. в ней поля и обусловившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на поставленные воп­росы не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию. Это убедительно подтверждает основ­ное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле.

Задачи

11.1. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускают­ся в керосин плотностью 0,8 г/см³. Какова должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и керосине был один и тот же? Диэлектричес­кая проницаемость керосина e=2. [1,6 г/см³]

11.2. На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверх­ностной плотностью s =1,5 нКл/см² расположена круглая пластинка. Плоскость пластин­ки составляет с линиями напряженности угол a=45°. Определить поток вектора напря­женности через эту пластинку, если ее радиус r=10 см. [1,88 кВ×м]

11.3. Кольцо радиусом r=10 см из тонкой проволоки равномерно заряжено с линейной плотностью t =10 нКл/м. Определить напряженность поля на оси, проходящей через центр кольца в точке А. удаленной на расстояние а =20 см от центра кольца. [1 кВ/м]

11.4. Шар радиусом R=10 см заряжен равномерно с объемной плотностью r =5 нКл/м³. Определить напряженность электростатического поля: 1) на расстоянии r₁=2 см от центра шара; 2) на расстоянии r₂=12 см от центра шара. Построить зависимость Е(r). [1) 3,77 В/м; 2) 13,1 В/м]

11.5. Электростатическое поле создается положительно заряженной бесконечной нитью с по­стоянной линейной плотностью t = 1 нКл/см. Какую скорость приобретет электрон, при­близившись под действием поля к нити вдоль линии напряженности с расстояния r₁=2,5 см до r₂=1,5 см? [18 Мм/с]

11.6. Электростатическое поле создается сферой радиусом R=4 см, равномерно заряжен­ной с поверхностной плотностью s =1 нКл/м². Определить разность потенциалов между двумя точками поля, лежащими на расстояниях r₁=6 см и r₂=10 см. [1,2 В]

11.7. Определить линейную плотность бесконечно длинной заряженной нити, если работа сил поля по перемещению заряда Q =1 нКл с расстояния r₁ =10 см до r₂ = 5 см в направле­нии, перпендикулярном нити, равна 0,1 мДж. [8 мкКл/м]

11.8. Пространство между обкладками плоского конденсатора заполнено парафином (e = 2). Расстояние между пластинами d=8,85 мм. Какую разность потенциалов необходимо подать на пластины, чтобы поверхностная плотность связанных зарядов на парафине составляла 0,05 нКл/см²? [500 В]

11.9. Свободные заряды равномерно распределены с объемной плотностью r =10 нКл/м³ по шару радиусом R = 5 см из однородного изотропного диэлектрика с диэлектрической проницаемостью e=6. Определить напряженности электростатического поля на расстоя­ниях r₁ = 2 см и r₂ = 10 см от центра шара. [E₁=1,25 В/м; E₂=23,5 В/м]

11.10. Пространство между пластинами плоского конденсатора заполнено стеклом (e = 7). Рас­стояние между пластинами d=5 мм, разность потенциалов U=500 В. Определить энер­гию поляризованной стеклянной пластины, если ее площадь S = 50 см². [6,64 мкДж]

11.11. Плоский воздушный конденсатор емкостью С=10 пФ заряжен до разности потенциа­лов U=1 кВ. После отключения конденсатора от источника напряжения расстояние между пластинами конденсатора было увеличено в два раза. Определить: 1) разность потенциалов на обкладках конденсатора после их раздвижения; 2) работу внешних сил по раздвижению пластин. [1) 2 кВ; 2) 5 мкДж]

11.12. Разность потенциалов между пластинами конденсатора U=200 В. Площадь каждой пластины S=100 см², расстояние между пластинами d=1 мм, пространство между ними заполнено парафином (e = 2). Определить силу притяжения пластин друг к другу. [3,54 мН]

Глава 12Постоянный электрический ток

§ 96. Электрический ток, сила и плотность тока

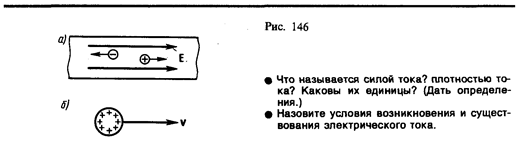
В электродинамике — разделе учения об электричестве, в котором рассматриваются явления и процессы, обусловленные движением электрических зарядов или макроско­пических заряженных тел, — важнейшим понятием является понятие электрического тока. Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. В проводнике под действием приложенного электрического поля Е свободные электрические заряды перемещаются: положительные — по полю, отрицательные — против поля (рис. 146, а), т. е. в проводнике возникает электричес­кий ток, называемый током проводимости. Если же упорядоченное движение электрических зарядов осуществляется перемещением в пространстве заряженного макроскопического тела (рис. 146, б), то возникает так называемый конвекционный ток.

Для возникновения и существования электрического тока необходимо, с одной стороны, наличие свободных носителей тока — заряженных частиц, способных переме­щаться упорядоченно, а с другой — наличие электрического поля, энергия которого, каким-то образом восполняясь, расходовалась бы на их упорядоченное движение. За направление тока условно принимают направление движения положительных зарядов.

Количественной мерой электрического тока служит сила тока I скалярная физи­ческая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени:

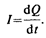
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока

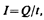
где Q — электрический заряд, проходящий за время t через поперечное сечение провод­ника. Единила силы тока — ампер (А).

Физическая величина, определяемая силой тока, проходящего через единицу площа­ди поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока:

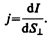
Выразим силу и плотность тока через скорость ávñ упорядоченного движения зарядов в проводнике. Если концентрация носителей тока равна n и каждый носитель имеет элементарный заряд е (что не обязательно для ионов), то за время dt через поперечное сечение S проводника переносится заряд dQ=ne ávñ S dt. Сила тока

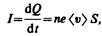
а плотность тока

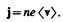(96.1)

Плотность тока — вектор, ориентированный по направлению тока, т. е. направление вектора j совпадает с направлением упорядоченного движения положительных зарядов. Единица плотности тока — ампер на метр в квадрате (А/м²).

Сила тока сквозь произвольную поверхность S определяется как поток вектора j, т. е.

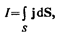(96.2)

где dS=ndS (n — единичный вектор нормали к площадке dS, составляющей с век­тором j угол a).

§ 97. Сторонние силы. Электродвижущая сила и напряжение

Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение носителей (они предполагаются положительными) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приведет к выравнива­нию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способ­ного создавать и поддерживать разность потенциалов за счет работы сил неэлект­ростатического происхождения. Такие устройства называютсяисточниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называютсясторонними.

Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и т. п. Роль источника тока в электрической цепи, образно говоря, такая же, как роль насоса, который необходим для перекачивания жидкости в гидравлической системе. Под действием создаваемого поля сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддерживается разность потенциалов и в цепи течет постоянный электрический ток.

Сторонние силы совершают работу по перемещению электрических зарядов. Физи­ческая величина, определяемая работой, совершаемой сторонними силами при переме­щении единичного положительного заряда, называетсяэлектродвижущей силой (э.д.с.),действующей в цепи:

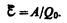(97.1)

Эта работа производятся за счет энергии, затрачиваемой в источнике тока, поэтому величину 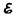можно также называть электродвижущей силой источника тока, включен­ного в цепь. Часто, вместо того чтобы сказать: «в цепи действуют сторонние силы», говорят: «в цепи действует э.д.с.», т. е. термин «электродвижущая сила» употребляет­ся как характеристика сторонних сил. Э.д.с., как и потенциал, выражается в вольтах (ср. (84.9) и (97.1)).