Тангенциальная составляющая ускорения 16 страница

Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы заря­дов можно провести бесчисленное множество. Однако их обычно проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверх­ностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности рас­положены гуще, напряженность поля больше.

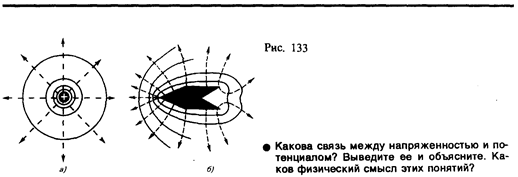
Итак, зная расположение линий напряженности электростатического поля, можно построить эквипотенциальные поверхности и, наоборот, по известному расположению эквипотенциальных поверхностей можно определить в каждой точке поля модуль и направление напряженности поля. На рис. 133 для примера показан вид линий напряженности (штриховые линии) и эквипотенциальных поверхностей (сплошные линии) полей положительного точечного заряда (а) и заряженного металлического цилиндра, имеющего на одном конце выступ, а на другом — впадину (б).

§ 86. Вычисление разности потенциалов по напряженности поля

Установленная в § 85 связь между напряженностью поля и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя произволь­ными точками этого поля.

1. Поле равномерно заряженной бесконечной плоскости определяется формулой (82.1): E=s/(2e₀), где s — поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях x₁ и х₂ от плоскости, равна (используем формулу (85.1))

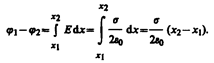
2. Поле двух бесконечных параллельных разноименно заряженных плоскостей определяется формулой (82.2); Е=s/e₀, где s — поверхностная плотность заряда. Разность потенциалов между плоско­стями, расстояние между которыми равно d (см. формулу (85.1)), равна

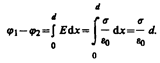(86.1)

3. Поле равномерно заряженной сферической поверхности радиуса R с общим зарядом Q вне сферы

(r> R) вычисляется по (82.3): 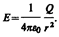Разностьпотенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от центра сферы (r₁ >R, r₂>R, r₂>r₁), равна

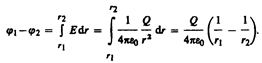(86.2)

Если принять r₁=r и r₂=¥, то потенциал поля вне сферической поверхности, согласно формуле (86.2), задается выражением

(ср. с формулой (84.5)). Внутри сферической поверхности потенциал всюду одинаков и равен

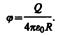
График зависимости j от r приведен на рис. 134.

4. Поле объемно заряженного шарарадиуса R с общим зарядом Q вне шара (r>R) вычисляется по формуле (82.3), поэтому разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от центра шара (r₁ > R, r₂ > R, r₂ > r₁), определяется формулой (86.2). 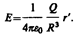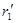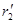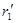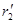В любой точке, лежащей внутри шара на расстоянии r' от его центра (r'<R), напряженность определяется выражением (82.4): Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях и от центра шара ( <R, <R, 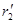> 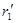), равна

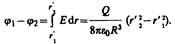
5. Поле равномерно заряженного бесконечного цилиндрарадиуса R, заряженного с линейной

плотностью t, вне цилиндра (r>R) определяется формулой (82.5): 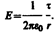Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r₁ м r₂ от оси заряженного цилиндра (r₁>R, r₂>R, r₂>r₁), равна

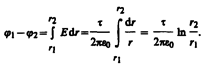(86.3)

§ 87. Типы диэлектриков. Поляризация диэлектриков

Диэлектрик (как и всякое вещество) состоит из атомов и молекул. Так как положитель­ный заряд всех ядер молекулы равен суммарному заряду электронов, то молекула в целом электрически нейтральна. Если заменить положительные заряды ядер молекул суммарным зарядом + Q, находящимся в центре «тяжести» положительных зарядов, а заряд всех электронов — суммарным отрицательным зарядом – Q, находящимся в центре «тяжести» отрицательных зарядов, то молекулу можно рассматривать как электрический диполь с электрическим моментом, определяемым формулой (80.3).

Первую группу диэлектриков (N₂, Н₂, О₂, СО₂, СН₄, ...) составляют вещества, молекулы которых имеют симметричное строение, т. е. центры «тяжести» положитель­ных и отрицательных зарядов в отсутствие внешнего электрического поля совпадают и, следовательно, дипольный момент молекулы р равен нулю.Молекулы таких диэлект­риков называютсянеполярными. Под действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные по полю, отрицательные против поля) и молекула приобретает дипольный момент.

Вторую группу диэлектриков (H₂O, NН₃, SO₂, CO,...) составляют вещества, молеку­лы которых имеют асимметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов не совпадают. Таким образом, эти молекулы в отсутствие внешнего электрического поля обладают дипольным моментом.Молекулы таких диэлектриков называютсяполярными. При отсутствии внешнего поля, однако, дипольные моменты полярных молекул вследствие теплового движения ориентированы в про­странстве хаотично и их результирующий момент равен нулю. Если такой диэлектрик поместить во внешнее поле, то силы этого поля будут стремиться повернуть диполи вдоль поля и возникает отличный от нуля результирующий момент.

Третью группу диэлектриков (NaCl, KCl, КВr, ...) составляют вещества, молекулы которых имеют ионное строение. Ионные кристаллы представляют собой простра­нственные решетки с правильным чередованием ионов разных знаков. В этих кри­сталлах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток. При наложении на ионный кристалл электрического поля происходит некоторая деформация кристаллической решетки или относительное смещение подрешеток, приводящее к возни­кновению дипольных моментов.

Таким образом, внесение всех трех групп диэлектриков во внешнее электрическое поле приводит к возникновению отличного от нуля результирующего электрического момента диэлектрика, или, иными словами, к поляризации диэлектрика.Поляризациейдиэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей.

Соответственно трем группам диэлектриков различают три вида поляризации:

электронная, илидеформационная, поляризация диэлектрика с неполярными молеку­лами, заключающаяся в возникновении у атомов индуцированного дипольного момен­та за счет деформации электронных орбит;

ориентационная, илидипольная, поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации имеющихся дипольных моментов молекул по полю. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрическое поле и тепловое движение) возникает преимущественная ориентация дипольных моментов молекул по полю. Эта ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура;

ионная поляризация диэлектриков с ионными кристаллическими решетками, заклю­чающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицатель­ных — против поля, приводящем к возникновению дипольных моментов.

§ 88. Поляризованность. Напряженность поля в диэлектрике

При помещении диэлектрика во внешнее электрическое поле он поляризуется, т. е. приобретает отличный от нуля дипольный момент 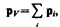гдер_i — дипольный момент одной молекулы. Для количественного описания поляризации диэлектрика пользуются векторной величиной —поляризованностью, определяемой как дипольный момент единицы объема диэлектрика:

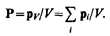(88.1)

Из опыта следует, что для большого класса диэлектриков (за исключением сегнетоэлектриков, см. § 91) поляризованность Р линейно зависит от напряженности поля Е. Если диэлектрик изотропный и Е не слишком велико, то

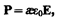(88.2)

где { —диэлектрическая восприимчивость вещества, характеризующая свойства ди­электрика; { – величина безразмерная; притом всегда { > 0 и для большинства диэлек­триков (твердых и жидких) составляет несколько единиц (хотя, например, для спирта {»25, для воды {=80).

Для установления количественных закономерностей поля в диэлектрике внесем в однородное внешнее электрическое поле Е₀ (создается двумя бесконечными парал­лельными разноименно заряженными плоскостями) пластинку из однородного диэлек­трика, расположив ее так, как показано на рис. 135. Под действием поля диэлектрик поляризуется, т. е. происходит смещение зарядов: положительные смещаются по полю, отрицательные — против поля. В результате этого на правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью +s', на левой — отрицательного заряда с поверхностной плотностью –s'. Эти нескомпенсированные заряды, появляющиеся в результате поля­ризации диэлектрика, называютсясвязанными. Так как их поверхностная плотность s' меньше плотности s свободных зарядов плоскостей, то не все поле Е компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть — обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внеш­ним полем. Вне диэлектрика Е=Е₀.

Таким образом, появление связанных зарядов приводит к возникновению допол­нительного электрического поля Е' (поля, создаваемого связанными зарядами), кото­рое направлено против внешнего поля Е₀ (поля, создаваемого свободными зарядами) и ослабляет его. Результирующее поле внутри диэлектрика

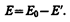
Поле Е'=s'/e₀ (поле, созданное двумя бесконечными заряженными плоскостями; см. формулу (82.2)), поэтому

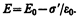(88.3)

Определим поверхностную плотность связанных зарядов s'. По (88.1), полный дипольный момент пластинки диэлектрика p_V =PV = PSd, где S — площадь грани пластинки, d — ее толщина. С другой стороны, полный дипольный момент, согласно (80.3), равен произведению связанного заряда каждой грани Q' =s' S на расстояние d между ними, т. е. р_V = s' Sd. Таким образом, PSd= s' Sd, или

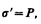(88.4)

т. е. поверхностная плотность связанных зарядов s' равна поляризованности Р. Подставив в (88.3) выражения (88.4) и (88.2), получим

откуда напряженность результирующего поля внутри диэлектрика равна

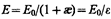(88.5)

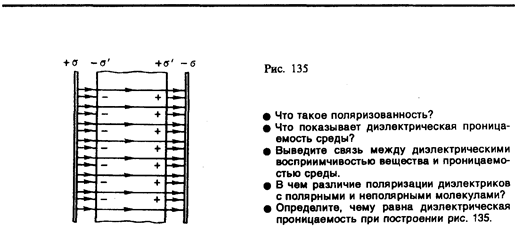
Безразмерная величина

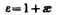(88.6)

называетсядиэлектрической проницаемостью среды. Сравнивая (88.5) и (88.6), видим, что e показывает, во сколько раз поле ослабляется диэлектриком, и характеризует количественно свойство диэлектрика поляризоваться в электрическом поле.

§ 88. Электрическое смещение. Теореме Гаусса для электростатического поля в диэлектрике

Напряженность электростатического поля, согласно (88.5), зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна e. Вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачко­образное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризо­вать поле ещевектором электрического смещения, который для электрически изотроп­ной среды, по определению, равен

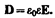(89.1)

Используя формулы (88.6) и (88.2), вектор электрического смещения можно выразить как

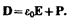(89.2)

Единица электрического смещения — кулон на метр в квадрате (Кл/м²).

Рассмотрим, с чем можно связать вектор электрического смещения. Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля, создаваемого системой свободных электрических зарядов, т. е. в диэлектрике на электростатическое поле свободных зарядов накладывается дополнительное поле свя­занных зарядов. Результирующее поле в диэлектрике описывается вектором напряжен­ности Е, и потому он зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, воз­никающие в диэлектрике, могут вызвать, однако, перераспределение свободных заря­дов, создающих поле. Поэтому вектор D характеризует электростатическое поле, создаваемое свободными зарядами (т. е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.

Аналогично, как и поле Е, поле D изображается с помощьюлиний электрического смещения, направление и густота которых определяются точно так же, как и для линий напряженности (см. §79).

Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.

Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверх­ность

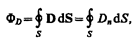
где D_n — проекция вектора D на нормаль n к площадке dS.

Теорема Гаусса дляэлектростатического поля в диэлектрике:

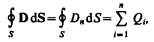(89.3)

т. е. поток вектора смещения электростатического поля в диэлектрике сквозь произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.

Для вакуума D_n = e₀E_n (e =1), тогда поток вектора напряженности Е сквозь произ­вольную замкнутую поверхность (ср. с (81.2)) равен

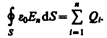
Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса (81.2) для поля Е в самом общем виде можно записать как

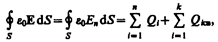
где 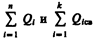— соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S. Однако эта формула неприемлема для описания поля Е в диэлектрике, так как она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз доказывает целесообразность введения вектора электрического смещения.

§ 90. Условия на границе раздела двух диэлектрических сред

Рассмотрим связь между векторами Е и D на границе раздела двух однородных изотропных диэлектриков (диэлектрические проницаемости которых e₁ и e₂) при отсут­ствии на границе свободных зарядов. Построим вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длины l, ориентировав его так, как показано на рис. 136. Согласно теореме (83.3) о циркуляции вектора Е,

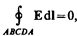
откуда

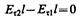
(знаки интегралов по АВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DA ничтожно малы). Поэтому

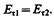(90.1)

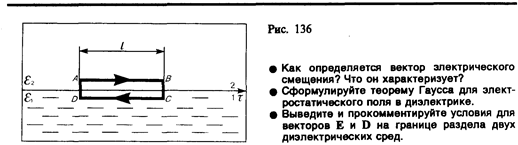
Заменив, согласно (89.1), проекции вектора Е проекциями вектора D, деленными на e₀e, получим

(90.2)

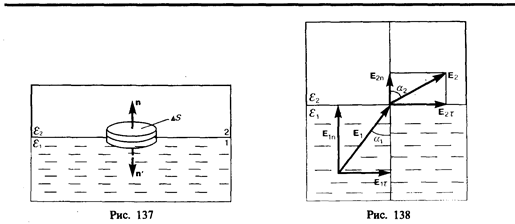
На границе раздела двух диэлектриков (рис. 137) построим прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом диэлектрике, другое — во втором. Основания DS настолько малы, что в пределах каждого из них вектор D одинаков. Согласно теореме Гаусса (89.3),

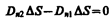
(нормалиnиn'к основаниям цилиндра направлены противоположно). Поэтому

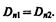(90.3)

Заменив, согласно (89.1), проекции вектора D проекциями вектора Е, умноженными на e₀e, получим

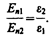(90.4)

Таким образом, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е (Е_t) и нормальная составляющая вектора D (D_n) изменяются непрерывно (не претерпевают скачка), а нормальная составляющая вектора Е (E_n) и тангенциальная составляющая вектора D (D_t) претерпевают скачок.

Из условий (90.1) — (90.4) для составляющих векторов Е и D следует, что линии этих векторов испытывают излом (преломляются). Найдем связь между углами a₁ и a₂ (на рис. 138 e₁>e₂). Согласно (90.1) и (90.4), Е_t2 = Е_t1 и e₂E_n2 = e₁E_n1. Разложим векторы E₁ и E₂ у границы раздела на тангенциальные и нормальные составляющие. Из рис. 138 следует, что

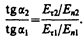
Учитывая записанные выше условия, получим закон преломления линий напряжен­ности Е (а значит, и линий смещения D)

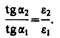
Эта формула показывает, что, входя в диэлектрик с большей диэлектрической проница­емостью, линии Е и D удаляются от нормали.

§ 91. Сегнетоэлектрики

Сегнетоэлектрики — диэлектрики, обладающие в определенном интервале температур спонтанной (самопроизвольной) поляризованностью, т. е. поляризованностью в отсут­ствие внешнего электрического поля. К сегнетоэлектрикам относятся, например, дета­льно изученные И. В. Курчатовым (1903—1960) и П. П. Кобеко (1897—1954) сегнетова соль NaKC₄H₄O₆ • 4Н₂О (от нее и получили свое название сегнетоэлектрики) и титанат бария ВаТiO₃.

При отсутствии внешнего электрического поля сегнетоэлектрик представляет собой как бы мозаикуиздоменов — областей с различными направлениями поляризованности. Это схематически показано на примере титаната бария (рис. 139), где стрелки и знаки , Å указывают направление вектора Р. Так как в смежных доменах эти направления различны, то в целом дипольный момент диэлектрика равен нулю. При внесении сегнетоэлектрика во внешнее поле происходит переориентация дипольных моментов доменов по полю, а возникшее при этом суммарное электрическое поле доменов будет поддерживать их некоторую ориентацию и после прекращения действия внешнего поля. Поэтому сегнетоэлектрики имеют аномально большие значения ди­электрической проницаемости (для сегнетовой соли, например, e_max»10⁴).

Сегнетоэлектрические свойства сильно зависят от температуры. Для каждого сег­нетоэлектрика имеется определенная температура, выше которой его необычные свой­ства исчезают и он становится обычным диэлектриком. Эта температура называется точкой Кюри (в честь французского физика Пьера Кюри (1859—1906)). Как правило, сегнетоэлектрики имеют только одну точку Кюри; исключение составляют лишь сегнетова соль (—18 и +24°С) и изоморфные с нею соединения. В сегнетоэлектриках вблизи точки Кюри наблюдается также резкое возрастание теплоемкости вещества. Превращение сегнетоэлектриков в обычный диэлектрик, происходящее в точке Кюри, сопровождается фазовым переходом II рода (см. § 75).

Диэлектрическая проницаемость e (а следовательно, и диэлектрическая восприим­чивость {) сегнетоэлектриков зависит от напряженности Е поля в веществе, а для других диэлектриков эти величины являются характеристиками вещества.

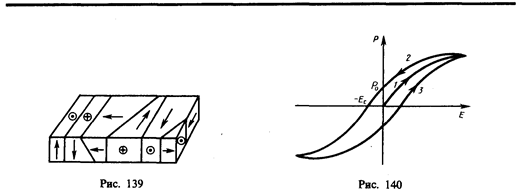
Для сегнетоэлектриков формула (88.2) не соблюдается; для них связь между векторами поляризованности (Р) и напряженности (Е) нелинейная и зависит от значений Е в предшествующие моменты времени. В сегнетоэлектриках наблюдаетсяявление диэлектрического гистерезиса («запаздывания»). Как видно из рис. 140, с увеличением напряженности Е внешнего электрического поля поляризованность Р растет, достигая насыщения (кривая 1). Уменьшение Р с уменьшением Е происходит по кривой 2, и при Е=0 сегнетоэлектрик сохраняетостаточную поляризованность Р₀, т.е. сегнетоэлектрик остается поляризованным в отсутствие внешнего электрического поля. Чтобы унич­тожить остаточную поляризованность, надо приложить электрическое поле обратного направления (—E_с). Величина Е_c называетсякоэрцитивной силой (от лат. coercitio — удерживание). Если далее Е изменять, то Р изменяется по кривой 3петли гистерезиса.

Интенсивному изучению сегнетоэлектриков послужило открытие академиком Б. М. Вулом (1903—1985) аномальных диэлектрических свойств титаната бария. Титанат бария из-за его химической устойчивости и высокой механической прочности, а также из-за сохранения сегнетоэлектрических свойств в широком температурном интервале нашел большое научно-техническое применение (например, в качестве гене­ратора и приемника ультразвуковых воли). В настоящее время известно более сотни сегнетоэлектриков, не считая их твердых растворов. Сегнетоэлектрики широко применяются также в качестве материалов, обладающих большими значениями e (например, в конденсаторах).

Следует упомянуть еще опьезоэлектриках — кристаллических веществах, в которых при сжатии или растяжении в определенных направлениях возникает электрическая поляризация даже в отсутст­вие внешнего электрического поля(прямой пьезоэффект). Наблюдаетсяиобратный пьезоэффект — появление механической деформации под действием электрического поля. У некоторых пьезоэлектриков решетка положительных ионов в состоянии термодинамического равновесия смеще­на относительно решетки отрицательных ионов, в результате чего они оказываются поляризован­ными даже без внешнего электрического поля. Такие кристаллы называются пироэлектриками. Еще существуютэлектреты — диэлектрики, длительно сохраняющие поляризованное состояние после снятия внешнего электрического поля (электрические аналоги постоянных магнитов). Эти группы веществ находят широкое применение в технике и бытовых устройствах.

§ 92. Проводники в электростатическом поле

Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии. Итак, напряженность поля во всех точках внутри проводника равна нулю:

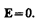
Отсутствие поля внутри проводника означает, согласно (85.2), что потенциал во всех точках внутри проводника постоянен (j = const), т. е. поверхность проводника в электростатическом поле является эквипотенциальной (см. § 85). Отсюда же следует, что вектор напряженности поля на внешней поверхности проводника направлен по нормали к каждой точке его поверхности. Если бы это было не так, то под действием касательной составляющей Е заряды начали бы по поверхности проводника переме­щаться, что, в свою очередь, противоречило бы равновесному распределению зарядов.

Если проводнику сообщить некоторый заряд Q, то нескомпенсированные заряды располагаются только на поверхности проводника. Это следует непосредственно из теоремы Гаусса (89.3), согласно которой заряд Q, находящийся внутри проводника в некотором объеме, ограниченном произвольной замкнутой поверхностью, равен

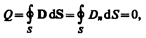
так как во всех точках внутри поверхности D=0.

Найдем взаимосвязь между напряженностью Е поля вблизи поверхности заряжен­ного проводника и поверхностной плотностью s зарядов на его поверхности. Для этого применим теорему Гаусса к бесконечно малому цилиндру с основаниями DS, пересека­ющему границу проводник — диэлектрик. Ось цилиндра ориентирована вдоль вектора Е (рис. 141). Поток вектора электрического смещения через внутреннюю часть цилинд­рической поверхности равен нулю, так как внутри проводника Е₁ (а следовательно, и D₁) равен нулю, поэтому поток вектора D сквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра. Со­гласно теореме Гаусса (89.3), этот поток (DDS) равен сумме зарядов (Q=sDS), охваты­ваемых поверхностью: DDS=sDS т.е.