Тангенциальная составляющая ускорения 3 страница

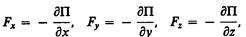
или в векторном виде

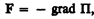(12.4)

где

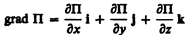(12.5)

(i, j, k — единичные векторы координатных осей). Вектор, определяемый выражением (12.5), называется градиентом скаляра П.

Для него наряду с обозначением grad П применяется также обозначение ÑП. Ñ («набла») означает символический вектор, называемыйоператором Гамильтона*илинабла-оператором:

(12.6)

* У. Гамильтон (1805—1865) — ирландский математик и физик.

Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, равна

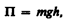(12.7)

где высота h отсчитывается от нулевого уровня, для которого П₀=0. Выражение (12.7) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.

Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина h' ), П= —mgh'.

Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:

где F_{x упp} — проекция силы упругости на ось х; k — коэффициент упругости (для пружины — жесткость), а знак минус указывает, что F_{x упp}направлена в сторону, противоположную деформации x.

По третьему закону Ньютона, деформирующая сила равна по модулю силе уп­ругости и противоположно ей направлена, т. е.

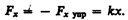
Элементарная работа dA, совершаемая силой F_x при бесконечно малой деформации dx, равна

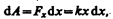
а полная работа

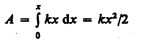
идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела

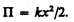
Потенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.

Полная механическая энергия системы — энергия механического движения и вза­имодействия:

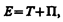
т. е. равна сумме кинетической и потенциальной энергий.

§ 13. Закон сохранения энергии

Закон сохранения энергии — результат обобщения многих экспериментальных данных. Идея этого закона принадлежит М. В. Ломоносову (1711—1765), изложившему закон сохранения материи и движения, а количественная формулировка закона сохранения энергии дана немецким врачом Ю. Майером (1814—1878) и немецким естествоиспыта­телем Г. Гельмгольцем (1821—1894).

Рассмотрим систему материальных точек массами m₁, m₂,..., m_n, движущихся со скоростями v₁, v₂,..., v_n. Пусть 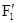, ,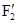..., 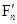— равнодействующие внутренних консер­вативных сил, действующих на каждую из этих точек, a F₁, F₂, ..., F_n — равнодейст­вующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначимf₁, f₂, ..., f_n. При v<<c массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие:

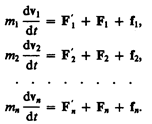
Двигаясь под действием сил, точки системы за интервал времени dt совершают перемещения, соответственно равные dr₁, dr₂, ..., dr_n. Умножим каждое из уравнений скалярно на соответствующее перемещение и, учитывая, что dr_i==v_i dt, получим

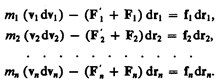
Сложив эти уравнения, получим

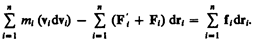(13.1)

Первый член левой части равенства (13.1)

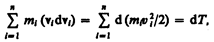
где dT — приращение кинетической энергии системы. Второй член равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии dП системы (см. (12.2)).

Правая часть равенства (13.1) задает работу внешних неконсервативных сил, дейст­вующих на систему. Таким образом,имеем

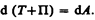(13.2)

При переходе системы из состояния 1 в какое-либо состояние 2

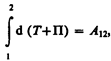
т. е. изменение полной механической энергии системы при переходе из одного состоя­ния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (13.2) следует, что

d (T+П) = 0,

откуда

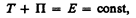(13.3)

т. е. полная механическая энергия системы сохраняется постоянной. Выражение (13.3) представляет собой закон сохранение механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия со­храняется, т. е. не изменяется со временем.

Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Закон сохранения механической энергии можно сформулировать так: в консервативных системах полная механическая энергия сохраняется.

Закон сохранения механической энергии связан с однородностью времени. Однород­ность времени проявляется в том, что физические законы инвариантны относительно выбора начала отсчета времени. Например, при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продо­лжительности свободного падения тела и не зависят от того, когда тело начало падать.

Существует еще один вид систем — диссипативные системы, в которых механичес­кая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации (или рассеяния) энергии. Строго говоря, все системы в природе являются диссипативными.

В консервативных системах полная механическая энергия остается постоянной. Могут происходить лишь превращения кинетической энергии в потенциальную и об­ратно в эквивалентных количествах так, что полная энергия остается неизменной. Этот закон не есть просто закон количественного сохранения энергии, а закон сохранения и превращения энергии, выражающий и качественную сторону взаимного превращения различных форм движения друг в друга. Закон сохранения и превращения энер­гии — фундаментальный закон природы, он справедлив как для систем макроскопичес­ких тел, так и для систем микротел.

В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезнове­нии» механической энергии всегда возникает эквивалентное количество энергии друго­го вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии — сущность неуничтожимости материи и ее движения.

§ 14. Графическом представление энергии

Во многих задачах рассматривается одномерное движение тела, потенциальная энергия которого является функцией лишь одной переменной (например, координаты х), т. е. П=П (х). График зависимости потенциальной энергии от некоторого аргумента назы­вается потенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела.

Будем рассматривать только консервативные системы, т. е. системы, в которых взаимные превращения механической энергии в другие виды отсутствуют. Тогда справедлив закон сохранения энергии в форме (13.3). Рассмотрим графическое пред­ставление потенциальной энергии для тела в однородном поле тяжести и для упругодеформированного тела.

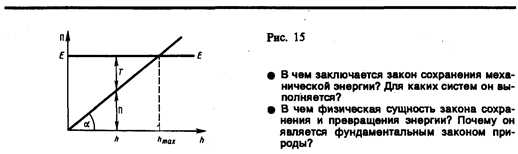
Потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, согласно (12.7), П (h)=mgh. График данной зависимости П = П(h) — прямая линия, проходящая через начало координат (рис. 15), угол наклона которой к оси h тем больше,чем больше масса тела (так как tga=mg).

Пусть полная энергия тела равна Е (ее график — прямая, параллельная оси h). На высоте h тело обладает потенциальной энергией П, которая определяется отрезком вертикали, заключенным между точкой h на оси абсцисс и графиком П(h). Естествен­но, что кинетическая энергия Т задается ординатой между графиком П(h) и горизон­тальной прямой ЕЕ. Из рис. 15 следует, что если h=h_max, то Т=0 и П=E=mgh_max, т. е.потенциальная энергия становится максимальной и равной полной энергии.

Из приведенного графика можно найти скорость тела на высоте h:

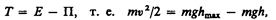
откуда

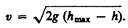
Зависимость потенциальной энергии упругой деформации П=кх²/2от деформации х имеет вид параболы (рис. 16), где график заданной полной энергии тела Е — прямая, параллельная оси абсцисс х, а значения Т и П определяются так же, как на рис. 15. Из рис. 16 следует, что с возрастанием деформации х потенциальная энергия тела воз­растает, а кинетическая — уменьшается. Абсцисса x_max определяет максимально воз­можную деформацию растяжения тела, a –х_max — максимально возможную дефор­мацию сжатия тела. Если х = ±х_max, то T=0 и П=E=k 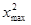/2, т. е. потенциальная энергия становится максимальной и равной полной энергии.

Из анализа графика на рис. 16 вытекает, что при полной энергии тела, равной Е, тело не может сместиться правее х_max и левее –х_max, так как кинетическая энергия не может быть отрицательной и, следовательно, потенциальная энергия не может быть больше полной энергии. В таком случае говорят, что тело находится впотенциальной яме с координатами – х_max £ x £ х_max.

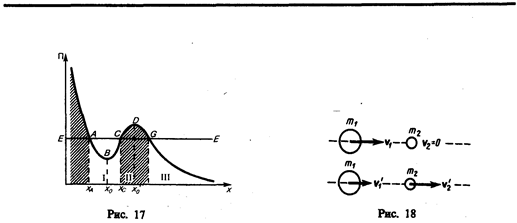
В общем случае потенциальная кривая может иметь довольно сложный вид, например с несколькими чередующимися максимумами и минимумами (рис. 17). Проанализируем эту потенциальную кривую. Если Е — заданная полная энергия частицы, то частица может находиться только там, где П(х) £ Е, т. е. в областях I и III. Переходить из области I в III и обратно частица не может, так как ей препятствует потенциальный барьер CDG, ширина которого равна интервалу значе­ний х, при которых E < П, а его высота определяется разностью П_mах–E. Для того чтобы частица смогла преодолеть потенциальный барьер, ей необходимо сообщить дополнительную энергию, равную высоте барьера или превышающую ее. В области I частица с полной энергией Е оказывается «запертой» в потенциальной яме AВС и совершает колебания между точками с координатами х_A и х_C.

В точке В с координатой х₀ (рис. 17) потенциальная энергия частицы минимальна. Так как действующая на частицу сила (см. § 12) 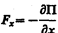(П — функция только одной координаты), а условие минимума потенциальной энергии 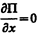, то в точке В —F_x = 0. При смещении частицы из положения х₀ (и влево и вправо) она испытывает действие возвращающей силы, поэтому положение х₀ является положениемустойчивого равновесия. Указанные условия выполняются и для точки 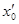(для П_max). Однако эта точка соответствует положениюнеустойчивого равновесия, так как при смещении частицы из положения 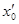появляется сила, стремящаяся удалить ее от этого положения.

§ 15. Удар абсолютно упругих и неупругих тел

Примером применения законов сохранения импульса и энергии при решении реальной физической задачи является удар абсолютно упругих и неупругих тел.

Удар (или соударение)—это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Помимо ударов в прямом смысле этого слова (столкновения атомов или биллиардных шаров) сюда можно отнести и такие, как удар человека о землю при прыжке с трамвая и т. д. Силы взаимодействия между сталкивающимися телами (ударные или мгновенные силы) столь велики, что внешними силами, действующими на них, можно пренебречь. Это позволяет систему тел в процес­се их соударения приближенно рассматривать как замкнутую систему и применять к ней законы сохранения.

Тела во время удара претерпевают деформацию. Сущность удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Наблюдения пока­зывают, что относительная скорость тел после удара не достигает своего прежнего значения. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей. Отношение нормальных составляющих относительной скорости тел после и да удара называется коэффициентом восстановления e:

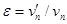
Если для сталкивающихся тел e=0, то такие тела называются абсолютно неупругими, если e=1 — абсолютно упругими. На практике для всех тел 0 < e < 1 (например, для стальных шаров e»0,56, для шаров из слоновой кости e»0,89, для свинца e»0). Однако в некоторых случаях тела можно с большой степенью точности рассматривать либо как абсолютно упругие, либо как абсолютно неупругие.

Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называетсялинией удара. Удар называетсяцентральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс. Мы будем рассматривать только центральные абсолютно упругие и абсолютно неупругие удары.

Абсолютно упругий удар — столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энер­гия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию (подчеркнем, что это идеализированный случай).

Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии.

Обозначим скорости шаров массами т₁ и m₂ до удара через v₁ и v₂, после удара—через 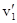и 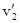(рис. 18). В случае прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей. Их направления учтем знаками: положительное значение припишем движению вправо, отрицатель-нос — движению влево.

При указанных допущениях законы сохранения имеют вид

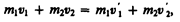(15.1)

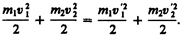(15.2)

Произведя соответствующие преобразования в выражениях (15.1) и (15.2), получим

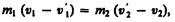(15.3)

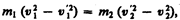(15.4)

откуда

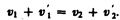(15.5)

Решая уравнения (15.3) и (15.5), находим

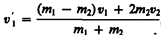(15.6)

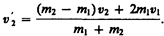(15.7)

Разберем несколько примеров.

1. При v₂=0

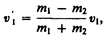(15.8)

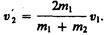(15.9)

Проанализируем выражения (15.8) в (15.9) для двух шаров различных масс:

а) т₁=т₂. Если второй шар до удара висел неподвижно (v₂=0) (рис. 19), то после удара остановится первый шар ( 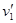=0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до удара ( );

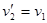б) т₁>т₂. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью ( 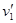<v₁). Скорость второго шара после удара больше, чем скорость первого после удара ( 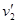> 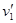) (рис. 20);

в) т₁<т₂. Направление движения первого шара при ударе изменяется—шар отскакивает обратно. Второй шар движется в ту же сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т. е. 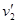<v₁ (рис. 21);

г) т₂>>т₁ (например, столкновение шара со стеной). Из уравнений (15.8) и (15.9) следует, что 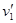= –v₁, 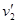»2m₁v₁/m₂»0.

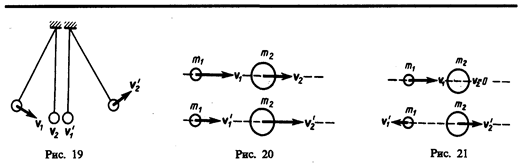
2. При т₁=т₂ выражения (15.6) и (15.7) будут иметь вид

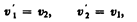
т. е. шары равной массы «обмениваются» скоростями.

Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстре­чу друг другу (рис. 22).

Если массы шаров т₁ и т₂, их скорости до удара v₁ и v₂, то, используя закон сохранения импульса, можно записать

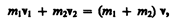
где v — скорость движения шаров после удара. Тогда

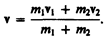(15.10)

Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае, если массы шаров равны (т₁=т₂), то

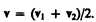
Выясним, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие не от самих деформаций, а от их скоростей, то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения механической энергии не должен соблюдаться. Вследствие деформации происходит «потеря» кинетической энергии, перешедшей в тепловую или другие формы энергии. Эту «потерю» можно определить по разности кинетической энергии тел до и после удара:

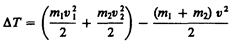
Используя (15.10), получаем

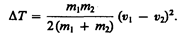
Если ударяемое тело было первоначально неподвижно (v₂=0), то

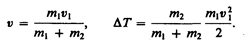
Когда m₂>>m₁ (масса неподвижного тела очень большая), то v<<v₁ и почти вся кинети­ческая энергия тела при ударе переходит в другие формы энергии. Поэтому, например, для получения значительной деформации наковальня должна быть массивнее молотка. Наоборот, при забивании гвоздей в стену масса молотка должна быть гораздо большей (m₁>>m₂), тогда v»v₁ и практически вся энергия затрачивается на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.

Абсолютно неупругий удар — пример того, как происходит «потеря» механической энергии под действием диссипативных сил.

Задачи

3.1. Определить: 1) работу поднятия груза по наклонной плоскости; 2) среднюю и 3) максималь­ную мощности подъемного устройства, еслимасса груза 10 кг, длина наклонной плоскости 2 м, угол ее наклона к горизонту 45°, коэффициент трения 0,1 и время подъема 2 с. [1) 173 Дж; 2) 86 Вт; 3) 173 Вт]

3.2.С башни высотой 35 м горизонтально брошен камень массой 0,3 кг. Пренебрегая со­противлением воздуха, определить: 1) скорость, с которой брошен камень, если через 1 с после начала движения его кинетическая энергия 60 Дж: 2) потенциальную энергию камня через 1 с после начала движения. [1) 17,4 м/с; 2) 88,6 Дж]

3.3. Пренебрегая трением, определить наименьшую высоту, с которой должна скатываться тележ­ка с человеком по желобу, переходящему в петлю радиусом 10 м, чтобы она сделала полную петлю и не выпала из желоба. [25 м]

3.4. Пуля массой m=10 г, летевшая горизонтально со скоростью v=500 м/с, попадает в балли­стический маятник длиной l=1 м и массой M=5 кг и застревает в нем. Определить угол отклонения маятника. [18°30']

3.5. Зависимость потенциальной энергии частицы в центральном силовом поле от расстояния r до центра поля задается выражением П (r) = 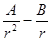, где А и В — положительные постоянные. Определить значение r₀, соответствующее равновесному положению частицы. Является ли это положение положением устойчивого равновесия? [r₀=2A/B]

3.6. При центральном абсолютно упругом ударе движущееся тело массой т₁ ударяется о по­коящееся тело массой m₂, в результате чего скорость первого тела уменьшается в n=1,5 ра­за. Определить: 1) отношение m₁/m₂; 2) кинетическую энергию Т₂ второго тела, если первоначальная кинетическая энергия первого тела T₁=1000 Дж. [1) 5; 2) 555 Дж]

3.7. Тело массой т₁=4 кг движется со скоростью v₁=3 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, определить количество теплоты, выделившееся при ударе. [9 Дж]

Глава 4 Механика твердого тела

§ 16. Момент инерции

При изучении вращения твердых тел будем пользоваться понятием момента инерции. Моментом инерциисистемы (тела) относительно данной оси называется физическая величина, равнаясумме произведений масс л материальных точек системы на квадраты их расстояний до рассматриваемой оси:

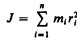
В случае непрерывного распределения масс эта сумма сводится к интегралу

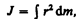
где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами х, у, z.

В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 23). Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r+dr. Момент инерции каждого полого цилиндра dJ=r²dm (так как dr<<r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm — масса всего элементарного цилиндра; его объем 2prhdr. Если r—плотность материала, то dm=2prhrdr и dJ=2phrr^зdr. Тогда момент инерции сплошного цилиндра

но так как pR²h — объем цилиндра, то его масса m=pR²hr, а момент инерции

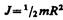
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями:

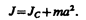(16.1)

В заключение приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, т — масса тела).

Таблица 1

§ 17. Кинетическая энергия вращения

Рассмотрим абсолютно твердое тело (см. § 1), вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массами т₁, т₂ ,..., т_n , находящиеся на расстоянии r₁, r₂,..., r_n от оси.