Тангенциальная составляющая ускорения 6 страница

Жидкость же, имея определенный объем, принимает форму того сосуда, в который она заключена. Но в жидкостях в отличие от газов среднее расстояние между молекула­ми остается практически постоянным, поэтому жидкость обладает практически неиз­менным объемом.

Единица давления —паскаль (Па): 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1м²(1 Па=1 Н/м²).

Давление при равновесии жидкостей (газов) подчиняетсязакону Паскаля*: давле­ние в любом месте покоящейся жидкости одинаково по воем направлениям, при­чем давление одинаково передается по всему объему, занятому покоящейся жидкос­тью.

* Б. Паскаль (1623—1662) — французский ученый.

Рассмотрим, как влияет вес жидкости на распределение давления внутри покоящей­ся несжимаемой жидкости. При равновесии жидкости давление по горизонтали всегда одинаково, иначе не было бы равновесия. Поэтому свободная поверхность покоящейся жидкости всегда горизонтальна вдали от стенок сосуда. Если жидкость несжимаема, то ее плотность не зависит от давления. Тогда при поперечном сечении S столба жид­кости, его высоте h и плотности r вес P=rgSh, а давление на нижнее основание

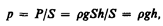(28.1)

т. е. давление изменяется линейно с высотой. Давление rgh называетсягидростатичес­ким давлением.

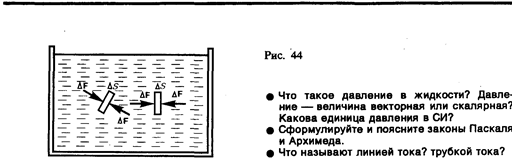
Согласно формуле (28.1), сила давления на нижние слои жидкости будет больше, чем на верхние, поэтому на тело, погруженное в жидкость, действует сила, определя­емая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа):

F_А=PgV,

где р — плотность жидкости, V— объем погруженного в жидкость тела.

§ 29. Уравнение неразрывности

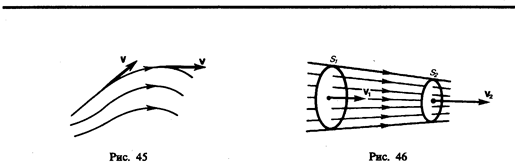
Движение жидкостей называется течением, а совокупность частиц движущейся жид­кости — потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 45). Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы.

Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.

Рассмотрим какую-либо трубку тока. Выберем два ее сечения S₁ и S₂, перпен­дикулярные направлению скорости (рис. 46).

За время Dt через сечение S проходит объем жидкости SvDt; следовательно, за 1 с через S₁ пройдет объем жидкости S₁v₁, где v₁ — скорость течения жидкости в месте сечения S₁. Через сечение S₂ за 1 с пройдет объем жидкости S₂v₂, где v₂ — скорость течения жидкости в месте сечения S₂. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (r=const), то через сечение S₂ пройдет такой же объем жидкости, как и через сечение S₁, т. е.

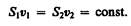(29.1)

Следовательно, произведение скорости течения несжимаемой жидкости на попереч­ное сечение трубки тока есть величина постоянная для данной трубки тока. Соотноше­ние (29.1) называетсяуравнением неразрывности для несжимаемой жидкости.

§ 30. Уравнение Бернулли и следствия из него

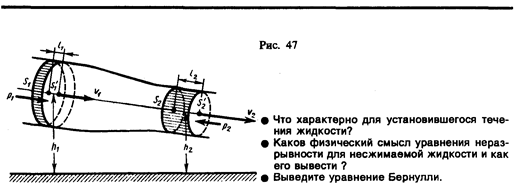
Выделим в стационарно текущей идеальной жидкости (физическая абстракция, т. е. воображаемая жидкость, в которой отсутствуют силы внутреннего трения) трубку тока, ограниченную сечениями S₁ и S₂, по которой слева направо течет жидкость (рис. 47). Пусть в месте сечения S₁ скорость течения v₁, давление p₁ и высота, на которой это сечение расположено, h₁. Аналогично, в месте сечения S₂ скорость течения v₂, давление p₂ и высота сечения h₂. За малый промежуток времени Dt жидкость перемеща­ется от сечения S₁ к сечению 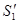, от S₂ к .

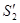Согласно закону сохранения энергии, изменение полной энергии E₂—E₁ идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы m жидкости:

E₂ – E₁ = А,(30.1)

где E₁ и E₂ — полные энергии жидкости массой m в местах сечений S₁ и S₂ соответст­венно.

С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S₁ и S₂, за рассматриваемый малый промежуток времени Dt. Для перенесения массы m от S₁ до 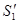жидкость должна переместиться на расстояние l₁=v₁Dt и от S₂ до 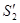— на расстояние l₂=v₂Dt. Отметим, что l₁ и l₂ настоль­ко малы, что всем точкам объемов, закрашенных на рис. 47, приписывают постоянные значения скорости v, давления р и высоты h. Следовательно,

А = F₁l₁ + F₂l₂, (30.2)

где F₁=p₁S₁ и F₂= – p₂S₂ (отрицательна, так как направлена в сторону, противополож­ную течению жидкости; рис. 47).

Полные энергии E₁ и E₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

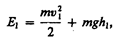(30.3)

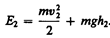(30.4)

Подставляя (30.3) и (30.4) в (30.1) и приравнивая (30.1) и (30.2), получим

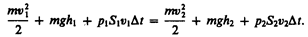(30.5)

Согласно уравнению неразрывности для несжимаемой жидкости (29.1), объем, занимаемый жидкостью, остается постоянным, т. е.

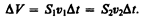
Разделив выражение (30.5) на DV, получим

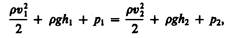
где р — плотность жидкости. Но так как сечения выбирались произвольно, то можем записать

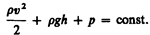(30.6)

Выражение (30.6) выведено швейцарским физиком Д. Бернулли (1700—1782; опуб­ликовано в 1738 г.) и называетсяуравнением Бернулли. Как видно из его вывода, уравнение Бернулли — выражение закона сохранения энергии применительно к устано­вившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико.

Величина р в формуле (30.6) называетсястатическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина rv²/2 —динамическим давлением. Как уже указывалось выше (см. § 28), величина rgh представляет собойгидростатическое давление.

Для горизонтальной трубки тока (h₁ =h₂) выражение (30.6) принимает вид

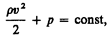(30.7)

где p+rv²/2 называетсяполным давлением.

Из уравнения Бернулли (30.7) для горизонтальной трубки тока и уравнения нераз­рывности (29.1) следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давле­ние больше в более широких местах, т. е. там, где скорость меньше. Это можно продемонстрировать, установив вдоль трубы рядманометров (рис. 48). В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикреп­ленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

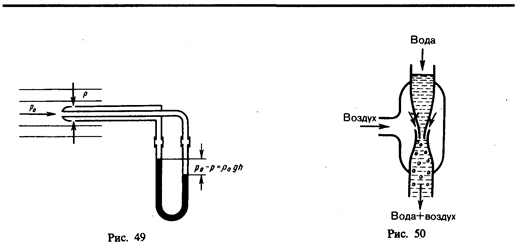
Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого приме­няется трубка Пито — Прандтля (рис. 49). Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. С помощью одной из трубок измеряется полное давление (р₀), с помощью дру­гой — статическое (р). Манометром измеряют разность давлений:

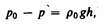(30.8)

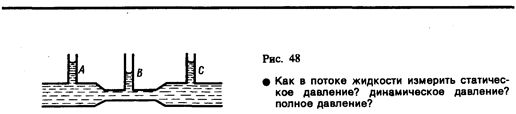
где ро — плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давле­нию:

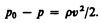(30.9)

Из формул (30.8) и (30.9) получаем искомую скорость потока жидкости:

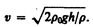
Уменьшение статического давления в точках, где скорость потока больше, положено в основу работыводоструйного насоса (рис. 50). Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавлива­ется и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. =133,32 Па).

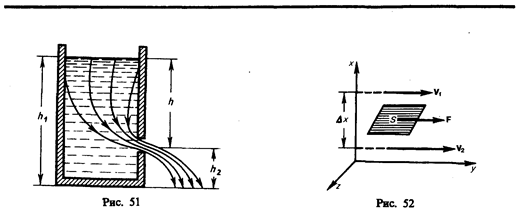
Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жид­костью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие (рис. 51).

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₂ выхода ее из отверстия) и напишем уравнение Бернулли:

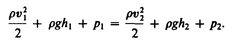
Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р₁=р₂, то уравнение будет иметь вид

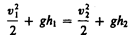
Из уравнения неразрывности (29.1) следует, что v₂/v₁=S₁/S₂, где S₁ и S₂ — площади поперечных сечений сосуда и отверстия. Если S₁>>S₂, то членом v 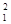/2 можно пренебречь и

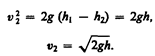
Это выражение получило название формулы Торричелли.*

* Э. Торричелли (1608—1647) — итальянский физик и математик.

§ 31. Вязкость (внутреннее трение). Ламинарный и турбулентный режимы течения жидкостей

Вязкость (внутреннее трение) — это свойство реальных жидкостей оказывать сопротив­ление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявля­ется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медлен­нее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

Сила внутреннего трения F тем больше, чем больше рассматриваемая площадь поверхности слоя S (рис. 52), и зависит от того, насколько быстро меняется скорость течения жидкости при переходе от слоя к слою. На рисунке представлены два слоя, отстоящие друг от друга на расстоянии Dx и движущиеся со скоростями v₁ и v₂. При этом v₁—v₂=Dv. Направление, в котором отсчитывается расстояние между слоями, перпендикулярно скорости течения слоев. Величина 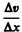показывает, как быстро меняется скорость при переходе от слоя к слою в направлении х, перпендикулярном направле­нию движения слоев, и называется градиентом скорости. Таким образом, модуль силы внутреннего трения

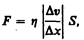(31.1)

где коэффициент пропорциональности m, зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью).

Единица вязкости — паскаль-секунда (Па×с): 1 Па×с равен динамической вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем, равным 1 м/с на 1 м, возникает сила внутреннего трения 1 Н на 1 м² поверхности касания слоев (1 Па×с= 1 Н×с/м²).

Чем больше вязкость, тем сильнее жидкость отличается от идеальной, тем большие силы внутреннего трения в ней возникают. Вязкость зависит от температуры, причем характер этой зависимости для жидкостей и газов различен (для жидкостей h с увеличе­нием температуры уменьшается, у газов, наоборот, увеличивается), что указывает на различие в них механизмов внутреннего трения. Особенно сильно от температуры зависит вязкость масел. Например, вязкость касторового масла в интервале 18—40°С падает в четыре раза. Российский физик П. Л. Капица (1894—1984; Нобелевская пре­мия 1978 г.) открыл, что при температуре 2,17 К жидкий гелий переходит в сверх­текучее состояние, в котором его вязкость равна нулю.

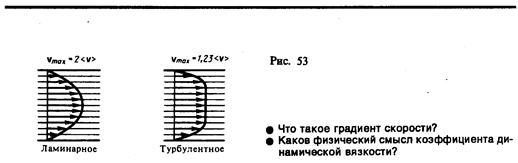
Существует два режима течения жидкостей. Течение называется ламинарным (слоис­тым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).

Ламинарное течение жидкости наблюдается при небольших скоростях ее движения. Внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным. Скоро­сти последующих слоев тем больше, чем больше их расстояние до поверхности трубы, и наибольшей скоростью обладает слой, движущийся вдоль оси трубы.

При турбулентном течении частицы жидкости приобретают составляющие скоро­стей, перпендикулярные течению, поэтому они могут переходить из одного слоя в другой. Скорость частиц жидкости быстро возрастает по мере удаления от поверх­ности трубы, затем изменяется довольно незначительно. Так как частицы жидкости переходят из одного слоя в другой, то их скорости в различных слоях мало отличают­ся. Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей.

Профиль усредненной скорости при турбулентном течении в трубах (рис. 53) отличается от параболического профиля при ламинарном течении более быстрым возрастанием скорости у стенок трубы и меньшей кривизной в центральной части течения. Характер течения зависит от безразмерной величины, называемойчислом Рейнольдса (О. Рейнольдс (1842—1912) — английский ученый):

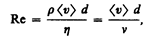
где n = h/p—кинематическая вязкость; р—плотность жидкости; <v>—средняя по сечению трубы скорость жидкости; d — характерный линейный размер, например диаметр трубы.

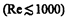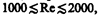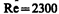При малых значениях числа Рейнольдса наблюдается ламинарное тече­ние, переход от ламинарного течения к турбулентному происходит в области а при (для гладких труб) течение—турбулентное. Если число Рейнольдса одинаково, то режим течения различных жидкостей (газов) в трубах разных сечений одинаков.

§ 32. Методы определения вязкости

1. Метод Стокса.* Этот метод определения вязкости основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы.

* Дж. Стокс (1819—1903) — английский физик и математик.

На шарик, падающий в жидкости вертикально вниз, действуют три силы: сила тяжести Р=⁴/₃pr³rg (r — плотность шарика), сила Архимеда Р=⁴/₃pr³r'g (r' — пло­тность жидкости) и сила сопротивления, эмпирически установленная Дж. Стоксом: F=6phrv, где r — радиус шарика, v — его скорость. При равномерном движении шарика

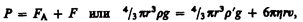
откуда

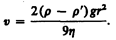
Измерив скорость равномерного движения шарика, можно определить вязкость жид­кости (газа).

2. Метод Пуазейля.* Этот метод основан на ламинарном течении жидкости в тонком капилляре. Рассмотрим капилляр радиусом R и длиной l. В жидкости мысленно выделим цилиндрический слой радиусом r и толщиной dr (рис. 54). Сила внутреннего трения (см. (31.1)), действующая на боковую поверхность этого слоя,

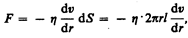
где dS — боковая поверхность цилиндрического слоя; знак минус означает, что при возрастании радиуса скорость уменьшается.

* Ж. Пуазейль (1799—1868) — французский физиолог и физик.

Для установившегося течения жидкости сила внутреннего трения, действующая на боковую поверхность цилиндра, уравновешивается силой давления, действующей на его основание:

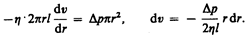
После интегрирования, полагая, что у стенок имеет место прилипание жидкости, т. е. скорость на расстоянии R от оси равна нулю, получаем

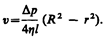
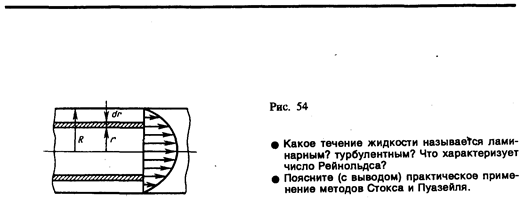
Отсюда видно, что скорости частиц жидкости распределяются по параболическому закону, причем вершина параболы лежит на оси трубы (см. также рис. 53).

За время t из трубы вытечет жидкость, объем которой

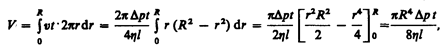
откуда вязкость

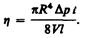
§ 33. Движение тел в жидкостях и газах

Одной из важнейших задач аэро- и гидродинамики является исследование движения твердых тел в газе и жидкости, в частности изучение тех сил, с которыми среда действует на движущееся тело. Эта проблема приобрела особенно большое значение в связи с бурным развитием авиации и увеличением скорости движения морских судов.

На тело, движущееся в жидкости или газе, действуют две силы (равнодействующую их обозначим R), одна из которых (R_x) направлена в сторону, противоположную движению тела (в сторону потока), —лобовое сопротивление, а вторая (R_y) перпен­дикулярна этому направлению —подъемная сила (рис. 55).

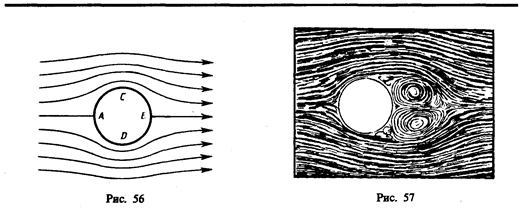
Если тело симметрично и его ось симметрии совпадает с направлением скорости, то на него действует только лобовое сопротивление, подъемная же сила в этом случае равна нулю. Можно доказать, что в идеальной жидкости равномерное движение происходит без лобового сопротивления. Если рассмотреть движение цилиндра в такой жидкости (рис. 56), то картина линий тока симметрична как относительно прямой, проходящей через точки А и В, так и относительно прямой, проходящей через точки С и D, т. с. результирующая сила давления на поверхность цилиндра будет равна нулю.

Иначе обстоит дело при движении тел в вязкой жидкости (особенно при увеличении скорости обтекания). Вследствие вязкости среды в области, прилегающей к поверх­ности тела, образуется пограничный слой частиц, движущихся с меньшими скоростями. В результате тормозящего действия этого слоя возникает вращение частиц и движение жидкости в пограничном слое становится вихревым. Если тело не имеет обтекаемой формы (нет плавно утончающейся хвостовой части), то пограничный слой жидкости отрывается от поверхности тела. За телом возникает течение жидкости (газа), направ­ленное противоположно набегающему потоку. Оторвавшийся пограничный слой, сле­дуя за этим течением, образует вихри, вращающиеся в противоположные стороны (рис. 57).

Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается безразмерным коэффициентом сопротивления С_x, определя­емым экспериментально:

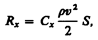(33.1)

где r — плотность среды; v — скорость движения тела; S — наибольшее поперечное сечение тела.

Составляющую R_x можно значительно уменьшить, подобрав тело такой формы, которая не способствует образованию завихрения.

Подъемная сила может быть определена формулой, аналогичной (33.1):

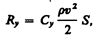
где С_у — безразмерный коэффициент подъемной силы.

Для крыла самолета требуется большая подъемная сила при малом лобовом сопротивлении (это условие выполняется при малых углах атаки a (угол к потоку); см. рис. 55). Крыло тем лучше удовлетворяет этому условию, чем больше величина К=С_у/С_x называемаякачеством крыла. Большие заслуги в конструировании требу­емого профиля крыла и изучении влияния геометрической формы тела на коэффициент подъемной силы принадлежат «отцу русской авиации» Н. Е. Жуковскому (1847—1921).

Задачи

6.1. Полый железный шар (r =7,87 г/см³) весит в воздухе 5 Н, а в воде (r' = 1 г/см³) — 3 Н. Пренебрегая выталкивающей силой воздуха, определить объем внутренней полости шара. [139 см³]

6.2. Бак цилиндрической формы площадью основания S = 1 м² и объемом V = 3 м³ заполнен водой. Пренебрегая вязкостью воды, определить время t, необходимое для опусто­шения бака, если на дне бака образовалось круглое отверстие площадью S₁ =10 см².

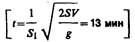
6.3. Сопло фонтана, дающего вертикальную струю высотой H = 5 м, имеет форму усеченного конуса, сужающегося вверх. Диаметр нижнего сечения d₁ = 6 см, верхнего — d₂ = 2 см. Вы­сота сопла h = 1 м. Пренебрегая сопротивлением воздуха в струе и сопротивлением в сопле, определить: 1) расход воды в 1 с, подаваемой фонтаном; 2) разность Dр давления в нижнем сечении и атмосферного давления. Плотность воды r =1 г/см³. [1) 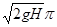d²/4 = 3,1 х 10^-3 м³/с; 2) Dp = pgh + pgH (1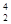– d /d 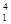=58,3 кПа]

6.4. На горизонтальной поверхности стоит цилиндрический сосуд, в боковой поверхности которого имеется отверстие. Поперечное сечение отверстия значительно меньше поперечного сечения самого сосуда. Отверстие расположено на расстоянии h₁ = 64 см ниже уровня воды в сосуде, который поддерживается постоянным, и на расстоянии h₂ = 25 см от дна сосуда. Пренебрегая вязкостью воды, определить, на каком расстоянии по горизонтали от сосуда падает на поверхность струя, вытекающая из отверстия. [80 см]

6.5. В широком сосуде, наполненном глицерином (плотность r =1,2 г/см³), падает с устано­вившейся скоростью 5 см/с стеклянный шарик (r' = 2,7 г/см³) диаметром 1 мм. Определить динамическую вязкость глицерина. [1,6 Па×с]

6.6. В боковую поверхность цилиндрического сосуда, установленного на столе, вставлен на высоте h₁ = 5 см от его дна капилляр внутренним диаметром d = 2 мм и длиной l = 1 см. В сосуде поддерживается постоянный уровеньмашинного масла (плотность r = 0,9 г/см³ и динамичес­кая вязкость h = 0,1 Па×с) на высоте h₂ = 80 см выше капилляра. Определить, на каком расстоянии по горизонтали от конца капилляра падает на поверхность стола струя масла, вытекающая из отверстия.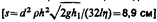

6.7. Определить наибольшую скорость, которую может приобрести свободно падающий в воз­духе (r=1,29 г/см³) стальной шарик (r' = 9 г/см³) массой m = 20 г. Коэффициент С_х принять равным 0,5. [94 см/с]

Глава 7 Элементы специальной (частной) теории относительности

§ 34. Преобразования Галилея. Механический принцип относительности

В классической механике справедливмеханический принцип относительности (принцип относительности Галилея): законы динамики одинаковы во всех инерциальных систе­мах отсчета.

Для его доказательства рассмотрим две системы отсчета: инерциальную систему K (с координатами х, у, z), которую условно будем считать неподвижной, и систему K' (с координатами x', у', z'), движущуюся относительно K равномерно и прямолинейно со скоростью u (u=const). Отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Пусть в произвольный момент времени t расположение этих систем друг относительно друга имеет вид, изображенный на рис. 58. Скорость u направлена вдоль OO', радиус-вектор, проведенный из О в О', r₀=ut.

Найдем связь между координатами произвольной точки А в обеих системах. Из рис. 58 видно, что

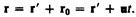(34.1)

Уравнение (34.1) можно записать в проекциях на оси координат: