Обратные тригонометрические функции.
Графики этих функций
y=arcsin x, y=arсcos x, y=arсtg x и y=arcctg x
приведены ниже.

Рис. 12. График функции у=arcsin x
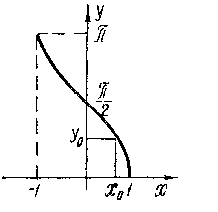

Рис. 13. График функции у=arccos x
Рис. 14. График функции у= arctg x
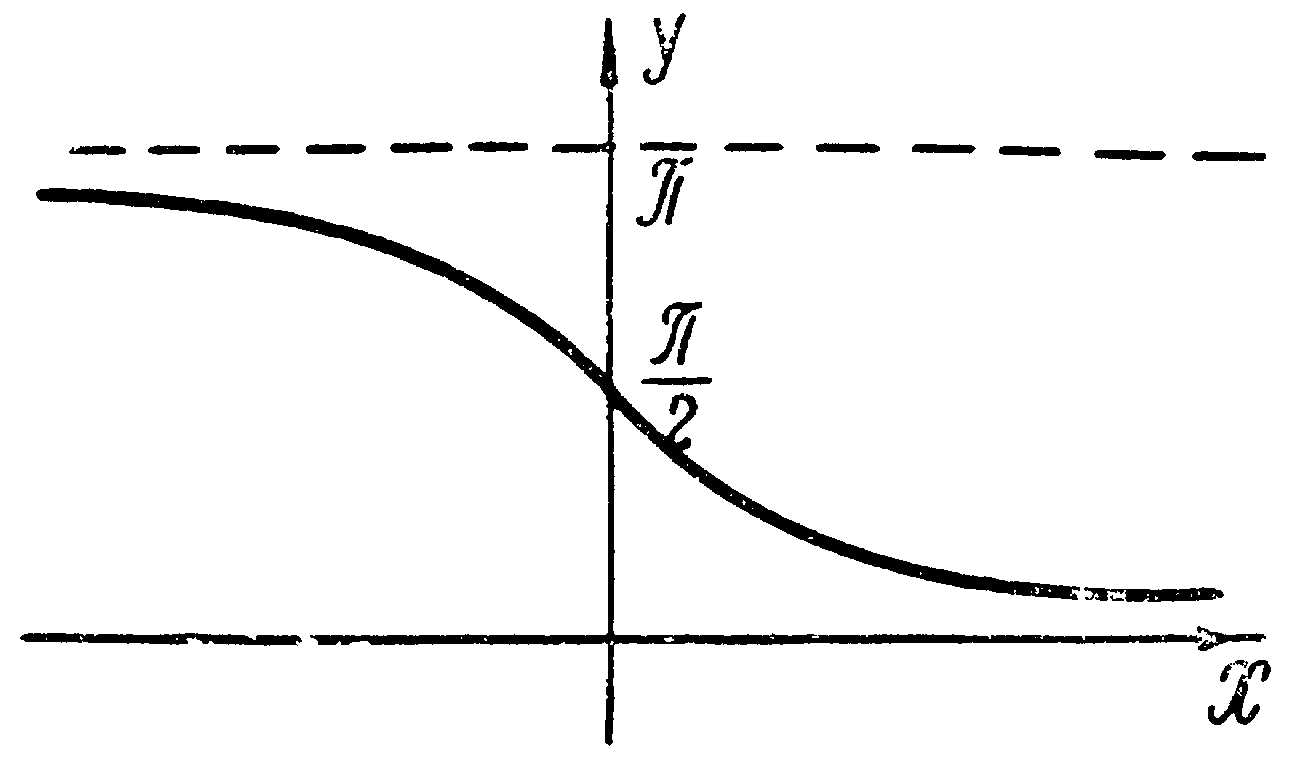
Рис. 15. График функции у=arcctg x
Все рассмотренные функции называют основными (или простейшими) элементарными функциями.
Рассмотрим сложные функции. Пусть функция у=ƒ(х) определена на множестве Х со значениями на множестве У. Пусть на множестве У задана функция z=φ(у), которая всякому значению х из Х сопоставляет значение переменной z, полученное через промежуточное значение переменной у. Поэтому z-функция переменной х:
z=φ(ƒ(х)),
с областью определения Х, но зависимость z от х осуществляется через посредство переменной у, которая называется промежуточным аргументом.Итак, переменная z здесь – функция от функции. Функцию такого рода называют сложной функцией (или суперпозицией функций).
Функции, записываемые с помощью конечного числа суперпозиций основных элементарных функций, называют элементарными функциями.
Примеры элементарных функций:
у=lg tg x,  , y=(1+cos23x)3.
, y=(1+cos23x)3.
Понятно, что чаще приходится иметь дело именно с элементарными функциями.
Дата добавления: 2014-12-30; просмотров: 1252;
