Предел и непрерывность функции. Понятие предела является основным понятием математического анализа

Понятие предела является основным понятием математического анализа. Использование предельного перехода является одной из отличительных черт высшей математики вообще и математического анализа в особенности.

Пусть функция у=ƒ(х) определена на некотором множестве Х и х₀ – некоторая точка из множества Х.

Определение. Число А называется пределом функции ƒ(х) при х, стремящемся к х₀, если для любой ε – окрестности точки А можно указать такую δ-окрестность точки х₀ (δ зависит от ε), что для любого х из δ-окрестности точки х₀ (х¹х₀) соответствующее значение функции ƒ(х) будет принадлежать ε–окрестности точки А.

Обозначают: .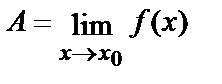

Читают: А является пределом функции ƒ(х) при х, стремящемся к х₀. Употребляется и такое обозначение предела функции: ƒ(х)®А при х®х₀.

Замечая, что δ-окрестностью точки х₀ называют интервал (х₀–δ, х₀+δ), ε-окрестностью точки А называют интервал (А–ε; А+ε), дадим еще одно определение предела функции.

Определение. Число А называется пределом функции ƒ(х) при х, стремящемся к х₀, если для любого положительного числа ε найдется такое положительное число δ, что неравенство

А–ε < ƒ(х) < А+ε

выполняется для любого х, отличного от х₀, удовлетворяющего неравенству

х₀–δ < х < х₀+δ.