Основные определения и способы задания ПФ
Вектор входных переменных переключательной функции 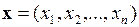 называется набором. Любой набор значений аргументов ПФ будем рассматривать как целое двоичное число, определяющее его номер при перечислении:
называется набором. Любой набор значений аргументов ПФ будем рассматривать как целое двоичное число, определяющее его номер при перечислении: 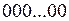 – «ноль» (нулевой набор),
– «ноль» (нулевой набор), 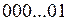 – «один» (первый набор),
– «один» (первый набор),  – «два» (второй набор), и т.д.
– «два» (второй набор), и т.д.
Поскольку общее число наборов равно 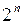 и на каждом из них ПФ может принимать одно из двух значений: 0 или 1, максимальное число различных переключательных функций, зависящих от n переменных, равно
и на каждом из них ПФ может принимать одно из двух значений: 0 или 1, максимальное число различных переключательных функций, зависящих от n переменных, равно 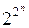 .
.
Любая ПФ, зависящая от n аргументов, может быть определена на 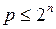 наборах. Если для некоторой функции
наборах. Если для некоторой функции 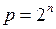 , то такая функция называется полностью определенной. В противном случае функция называется не полностью определенной.
, то такая функция называется полностью определенной. В противном случае функция называется не полностью определенной.
Пусть s – число наборов, на которых значение функции не определено. Не полностью определенную функцию можно доопределить значениями 0 или 1 на всех s наборах, при этом выбор совокупности значений функции может определяться произвольно или исходя из каких-либо рациональных соображений. Таким образом, при произвольном доопределении не полностью определенной функции можно получить  различных полностью определенных функций.
различных полностью определенных функций.
Переключательную функцию можно задать одним из трех способов: аналитическим, геометрическим или матричным [4]. Простейшей разновидностью матричного способа задания является составление таблицы истинности ПФ. Таблица истинности булевой функции представляет собой совокупность наборов входных аргументов и соответствующие этим наборам выходные значения задаваемой функции (табл. 3.1).
Таблица 3.1
| № набора | ||||||||||||||||
| x1 | ||||||||||||||||
| x2 | ||||||||||||||||
| x3 | ||||||||||||||||
| x4 | ||||||||||||||||
| f1(x1, x2, x3, x4) | ||||||||||||||||
| f2(x1, x2, x3, x4) | ||||||||||||||||
| f3(x1, x2, x3, x4) |
Задание ПФ при помощи таблицы истинности не всегда удобно, так как размеры таблицы растут пропорционально 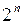 , где n – количество входных переменных.
, где n – количество входных переменных.
При аналитическом способе задания ПФ определяемая функция описывается выражениями с использованием последовательностей входных переменных и операций алгебры логики (более подробно этот способ задания ПФ рассматривается в разделе 3.5).
Рассмотрим геометрический способ задания ПФ. Каждый двоичный набор n переменных 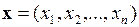 в геометрическом смысле можно интерпретировать как вектор единичной длины, определяющий точку
в геометрическом смысле можно интерпретировать как вектор единичной длины, определяющий точку
n-мерного пространства. Таким образом, множество 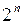 наборов определяет множество вершин n-мерного гиперкуба. Для
наборов определяет множество вершин n-мерного гиперкуба. Для  на рис. 3.1 представлен трехмерный куб, где каждой вершине соответствует один из возможных наборов входных переменных. Для задания ПФ графическим
на рис. 3.1 представлен трехмерный куб, где каждой вершине соответствует один из возможных наборов входных переменных. Для задания ПФ графическим
способом необходимо определить ее значения в вершинах n-мерного гиперкуба.

Переключательная функция называется существенно зависящей от переменной 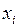 , если хотя бы для одного набора переменных
, если хотя бы для одного набора переменных 
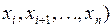 выполняется следующее соотношение:
выполняется следующее соотношение:
 .
.
Если такое соотношение не выполняется, то функция 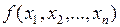 не зависит от переменной
не зависит от переменной 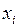 . В этом случае переменная
. В этом случае переменная 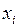 называется фиктивной. Фиктивные переменные можно исключить, так как от этого значения функции не изменяются.
называется фиктивной. Фиктивные переменные можно исключить, так как от этого значения функции не изменяются.
Один из способов определения фиктивных переменных заключается в следующем. Разобьем множество наборов входных переменных на два подмножества. В первое подмножество входят наборы, на которых функция принимает значение 1, а во второе подмножество входят наборы, на которых функция принимает значение 0. Для проверки фиктивности переменной 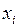 необходимо вычеркнуть соответствующие ей столбцы из обоих подмножеств. Отсутствие в подмножествах одинаковых наборов указывает на фиктивность аргумента
необходимо вычеркнуть соответствующие ей столбцы из обоих подмножеств. Отсутствие в подмножествах одинаковых наборов указывает на фиктивность аргумента 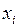 .
.
В качестве примера рассмотрим функцию f3, заданную табл. 3.1. Разобьем множество ее аргументов на два подмножества (табл. 3.2, 3.3). Вычеркнем в этих таблицах столбцы, соответствующие переменной x4. Поскольку в таблицах отсутствуют одинаковые наборы, можно сделать вывод, что переменная x4 является фиктивной.
Таблица 3.2 Таблица 3.3
| x1 | x2 | x3 | x4 | x1 | x2 | x3 | x4 | |
f3(x1, x2, x3, x4) = 1 f3(x1, x2, x3, x4) = 0
Дата добавления: 2014-12-27; просмотров: 1278;
