Деление в D-кодах

По причине больших временных затрат алгоритм деления в D-кодах с восстановлением остатка обычно не реализуется в цифровых вычислительных устройствах, поэтому здесь будем рассматривать только алгоритм деления без восстановления остатка. В качестве упражнения читателю может быть предложено самостоятельно выполнить рассматриваемую арифметическую операцию с восстановлением и без восстановления остатка и оценить разницу в количестве выполняемых действий.

Рассмотрим следующую методику выполнения операции деления. Знак частного определяется в результате анализа знаков операндов по обычным правилам арифметики, после чего оба операнда делаются положительными. Чтобы исключить ситуацию с переполнением, будем рассматривать случай, когда модуль делимого меньше модуля делителя. Поскольку в рассматриваемом алгоритме делитель сдвигается вправо, для его хранения необходимо использовать регистр с k дополнительными двоичными разрядами; k определяется из неравенства , где m – число двоичных разрядов в представлении операндов. Очевидно, в сумматоре, содержащем делимое и частичные остатки, также должны быть предусмотрены k дополнительных разрядов. Учитывая особенности представления чисел в D-кодах, число дополнительных разрядов, определяемое вышеприведенным неравенством, при необходимости должно быть увеличено до образования соответствующего числа двоично-десятичных тетрад. Помимо сумматора и двух регистров (частного и делителя) устройство также должно содержать счетчик, используемый для формирования цифр частного.

Для получения n цифр частного необходимо выполнить n циклов деления. В первом такте каждого цикла содержимое регистра делителя сдвигается вправо на один десятичный разряд, а содержимое регистра частного сдвигается на один десятичный разряд влево. При этом в младший разряд регистра частного заносится текущее содержимое счетчика. Циклы делятся на четные и нечетные. Перед началом выполнения нечетных циклов в счетчике устанавливается цифра 0. Затем выполняется вычитание делителя до тех пор, пока содержимое сумматора не изменит знак на противоположный. В каждом такте вычитания (кроме последнего, соответствующего изменению знака) содержимое счетчика увеличивается на единицу. Перед началом выполнения четных циклов в счетчике устанавливается цифра 9. Затем выполняется прибавление делителя до тех пор, пока содержимое сумматора не изменит знак. В каждом такте сложения (кроме последнего) содержимое счетчика уменьшается на единицу. После выполнения n циклов необходимо выполнить действия, соответствующие первому такту -го цикла, для передачи последней определенной цифры частного из счетчика в соответствующий регистр.

Пример.

Операнды представим в D-коде 8421+3.

; ;

.

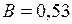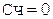
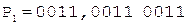
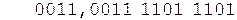Коррекция

(окончание примера на следующей странице)

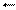
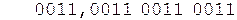Коррекция

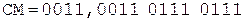
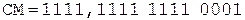
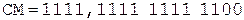
Коррекция

Коррекция

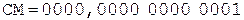
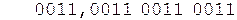Коррекция

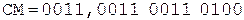
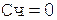
Таким образом, .

Вопросы для самоконтроля

1. В чем заключаются основные этапы выполнения операции сложения? Чем отличается выполнение операции вычитания?

2. В чем заключаются основные этапы выполнения операции умножения прямых кодов чисел? В чем различие методов умножения старшими и младшими разрядами вперед?

3. В чем заключаются основные этапы рассмотренных методов ускоренного выполнения операции умножения?

4. Чем отличается умножение инверсных кодов чисел от умножения прямых кодов?

5. В чем заключаются основные этапы выполнения операции деления прямых кодов чисел? В чем различие методов деления с восстановлением и без восстановления остатка?

6. В чем заключаются основные этапы рассмотренных методов ускоренного выполнения операции деления?

7. Чем отличается деление инверсных кодов чисел от деления прямых кодов?

8. В чем заключаются основные этапы выполнения операции извлечения квадратного корня? В чем различие методов с восстановлением и без восстановления остатка?

9. Особенности выполнения арифметических операций в D-кодах.