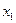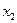Элементарные логические функции. Существуют четыре различные ПФ, зависящие от одного аргумента
Существуют четыре различные ПФ, зависящие от одного аргумента. При этом для функций 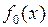 и
и 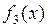 аргумент x является фиктивным (табл. 3.4).
аргумент x является фиктивным (табл. 3.4).
Таблица 3.4
 \ x \ x
| Условное обозначение | Название функции | ||
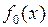
| Константа 0 | |||
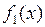
| 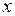
| Переменная х | ||
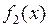
| 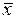
| Инверсия х | ||
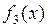
| Константа 1 |
Существуют 16 различных ПФ, зависящих от двух аргументов (табл. 3.5). При этом для функций  и
и 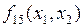 оба аргумента
оба аргумента 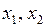 являются фиктивными, а для функций
являются фиктивными, а для функций 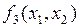 ,
, 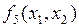 ,
, 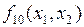 и
и 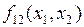 один из аргументов является фиктивным.
один из аргументов является фиктивным.
|

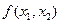
| Условное обозначение | Название функции | ||||
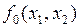
| Константа 0 | |||||

| 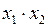
| Конъюнкция | ||||
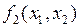
| 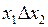
| Запрет по 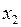
| ||||
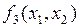
| 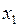
| Переменная 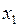
| ||||

| 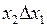
| Запрет по 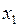
| ||||
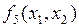
| 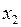
| Переменная 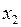
| ||||

| 
| Сложение по модулю 2 | ||||

| 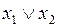
| Дизъюнкция | ||||
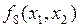
| 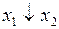
| Стрелка Пирса | ||||
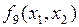
| 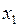 ~ ~ 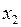
| Эквивалентность | ||||
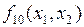
| 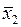
| Инверсия 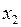
| ||||
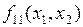
| 
| Импликация 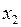 в в 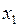
| ||||
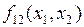
| 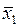
| Инверсия 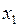
| ||||

| 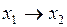
| Импликация 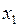 в в 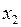
| ||||
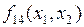
| 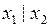
| Штрих Шеффера | ||||
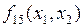
| Константа 1 |
Все ПФ одного аргумента, а также функции двух аргументов с номерами 1, 6, 7, 8, 9, 11, 14 называют элементарными и используют для построения более сложных функций путем изменения номеров аргументов и с помощью суперпозиции, т.е. подстановки вместо аргументов других переключательных функций.
Дата добавления: 2014-12-27; просмотров: 884;