Полные системы переключательных функций
Одной из наиболее важных задач, решаемой в процессе синтеза комбинационной схемы, является рациональный выбор логических элементов, которые будут использоваться при технической реализации логических схем. Поэтому основное требование, предъявляемое к набору логических элементов, заключается в том, что на основе этого набора элементов, реализующих элементарные логические функции, можно построить комбинационную схему, реализующую произвольную ПФ или (в общем случае) систему ПФ.
Следовательно, система логических функций, описывающих синтезируемую КС, должна быть представлена в виде переключательных функций, реализуемых выбранным набором логических элементов.
Система ПФ 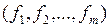 называется функционально полной, если любую булеву функцию произвольной сложности можно записать в виде формулы с использованием функций этой системы
называется функционально полной, если любую булеву функцию произвольной сложности можно записать в виде формулы с использованием функций этой системы 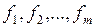 .
.
Функционально полная система ПФ называется базисом. Наибольшее распространение получили базисы {И, ИЛИ, НЕ}, {И-НЕ} (штрих Шеффера), {ИЛИ-НЕ} (стрелка Пирса).
Минимальным базисом называется такой базис, для которого исключение хотя бы одной из функций, образующих этот базис, превращает систему переключательных функций в неполную.
Базис может быть образован элементарными функциями, удовлетворяющими условиям теоремы Поста – Яблонского.
Теорема. Для того, чтобы система элементарных ПФ была функционально полной, необходимо и достаточно, чтобы она включала хотя бы одну функцию, не сохраняющую ноль, не сохраняющую единицу, не самодвойственную, не монотонную, не линейную.
Доказательство этой теоремы можно найти в [6].
Сформулируем ряд определений для классов переключательных функций, упоминаемых в теореме Поста – Яблонского.
Первый класс составляют функции, сохраняющие константу 0. Для таких функций должно выполняться условие 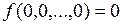 .
.
Второй класс составляют функции, сохраняющие константу 1. Для таких функций должно выполняться условие 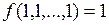 .
.
Третий класс составляют самодвойственные функции, которые на паре противоположных аргументов принимают противоположные значения. Для самодвойственных функций выполняется следующее равенство: 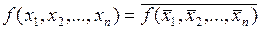 . Примером такой функции может служить отрицание.
. Примером такой функции может служить отрицание.
Четвертый класс составляют линейные ПФ. Линейной ПФ называется функция, которая может быть представлена полиномом по модулю 2 первой степени. В общем виде линейная ПФ может быть записана следующим образом: 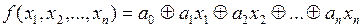 , где
, где 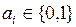 ,
, 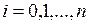 .
.
Пятый класс составляют монотонные ПФ. Введем критерий сравнения двух наборов аргументов. Два набора аргументов называются сравнимыми, если значение каждого аргумента одного набора больше или равно значению соответствующих аргументов второго набора, т.е. 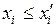 ,
, 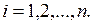
Монотонной называется такая ПФ, для которой при любом возрастании набора значения этой функции не убывают, т.е. 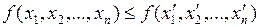 .
.
Принадлежность некоторых элементарных функций к тому или иному классу представлена в табл. 3.6. На пересечении строки и столбца поставлена отметка, если данная элементарная ПФ принадлежит к указанному классу.
Таблица 3.6
 Класс
ПФ Класс
ПФ
| Сохр. 0 | Сохр. 1 | Самодвойст- венная | Монотонная | Линейная |
| Константа 0 | Ú | Ú | Ú | ||
| Конъюнкция | Ú | Ú | Ú | ||
| Дизъюнкция | Ú | Ú | Ú | ||
| Сложение по модулю 2 | Ú | Ú |
Окончание табл. 3.6
| Эквивалентность | Ú | Ú | |||
| Стрелка Пирса | |||||
| Штрих Шеффера | |||||
| Импликация | Ú | ||||
| Отрицание | Ú | Ú | |||
| Константа 1 | Ú | Ú | Ú |
Из приведенной таблицы следует, что канонический базис булевой алгебры И-ИЛИ-НЕ, включающий конъюнкцию, дизъюнкцию и отрицание, является функционально полным, соответствующим требованиям теоремы Поста – Яблонского. Такой базис не является минимальным, так как из него без ущерба для полноты системы ПФ можно исключить конъюнкцию либо дизъюнкцию. При этом получаются системы ПФ, эквивалентные базисам И-НЕ, ИЛИ-НЕ.
Из табл. 3.6 можно получить, например, следующие минимальные базисы.
Базисы, состоящие из одной элементарной ПФ:
1) стрелка Пирса;
2) штрих Шеффера.
Базисы, состоящие из двух элементарных ПФ:
1) отрицание, конъюнкция;
2) константа 0, импликация;
3) отрицание, дизъюнкция.
3.5. Канонические формы
аналитического представления ПФ
Конституентой единицы называется функция, принимающая значение 1 только на одном наборе переменных. Конституента единицы записывается как логическое произведение n различных переменных, некоторые из которых или все могут быть с отрицаниями.
Конституентой нуля называется функция, принимающая значение 0 на единственном наборе переменных. Конституента нуля записывается как логическая сумма n различных переменных, часть которых или все могут быть с отрицаниями.
Любую конституенту 1 можно записать в виде конъюнкции всех ее аргументов, при этом переменная 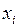 записывается с инверсией, если в наборе, на котором функция принимает значение 1, переменная
записывается с инверсией, если в наборе, на котором функция принимает значение 1, переменная 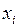 принимает значение 0. Например, логическое произведение
принимает значение 0. Например, логическое произведение 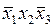 соответствует конституенте 1, принимающей единичное значение на наборе
соответствует конституенте 1, принимающей единичное значение на наборе 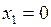 ,
, 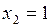 ,
, 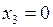 . На всех остальных наборах, как следует из определения, конституента 1 принимает значение 0. Вышеприведенное утверждение может быть доказано, например, методом перебора.
. На всех остальных наборах, как следует из определения, конституента 1 принимает значение 0. Вышеприведенное утверждение может быть доказано, например, методом перебора.
Каждому i-му набору аргументов 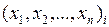 поставим в соответствие конституенту единицы
поставим в соответствие конституенту единицы 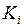 , принимающую единичное значение только на этом наборе.
, принимающую единичное значение только на этом наборе.
Любую переключательную функцию, зависящую от n аргументов, можно представить в виде разложения Шеннона:
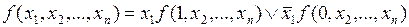 .
.
Произведем разложение Шеннона по всем переменным:
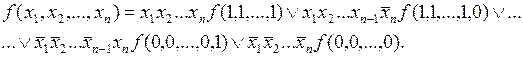
В полученном выражении заменим наборы аргументов, представленных конъюнкциями переменных, на соответствующие конституенты 1. Тогда переключательная функция в общем виде может быть представлена следующим образом:
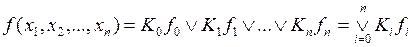 ,
,
где 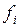 – значение функции на i-м наборе.
– значение функции на i-м наборе.
Воспользовавшись тем, что 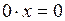 и
и 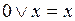 , в последнем выражении можно исключить слагаемые, для которых
, в последнем выражении можно исключить слагаемые, для которых 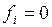 . Учитывая, что
. Учитывая, что 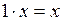 , можно не писать коэффициенты
, можно не писать коэффициенты 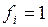 .
.
Таким образом, искомую функцию 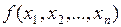 можно представить в виде дизъюнкции конституент 1, соответствующих наборам аргументов, на которых она принимает значение 1. Такая форма записи называется совершенной дизъюнктивной нормальной формой (СДНФ). Такое название объясняется тем, что каждый дизъюнктивный член включает в себя произведение всех n аргументов (совершенная форма) и каждое произведение является элементарным, т.е. под знаком инверсии могут быть только отдельные переменные (нормальная форма).
можно представить в виде дизъюнкции конституент 1, соответствующих наборам аргументов, на которых она принимает значение 1. Такая форма записи называется совершенной дизъюнктивной нормальной формой (СДНФ). Такое название объясняется тем, что каждый дизъюнктивный член включает в себя произведение всех n аргументов (совершенная форма) и каждое произведение является элементарным, т.е. под знаком инверсии могут быть только отдельные переменные (нормальная форма).
В качестве примера рассмотрим процедуру записи СДНФ логической функции 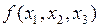 , заданной таблицей истинности (табл. 3.7). Для представления этой функции в виде СДНФ необходимо выполнить следующие действия, основанные на вышеприведенных рассуждениях.
, заданной таблицей истинности (табл. 3.7). Для представления этой функции в виде СДНФ необходимо выполнить следующие действия, основанные на вышеприведенных рассуждениях.
Таблица 3.7
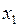
| ||||||||
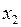
| ||||||||
| ||||||||
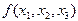
|
На первом этапе запишем функцию в виде дизъюнкции конституент единицы, соответствующих тем наборам, на которых функция принимает значение 1:
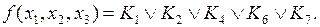
Затем, выразив конституенты единицы через произведения аргументов, получим искомую СДНФ:
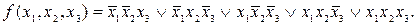
Из СДНФ функции и СДНФ ее отрицания, используя законы де Моргана, можно получить еще семь канонических форм.
Другой канонической формой записи является совершенная конъюнктивная нормальная форма (СКНФ). Ее отличие от СДНФ заключается в том, что СКНФ записывается как конъюнкция конституент нуля, соответствующих тем наборам, на которых функция принимает значение 0. При этом конституенты 0 записываются в виде элементарных дизъюнкций аргументов xi, инверсии которых соответствуют единичному значению аргумента.
Для примера запишем СКНФ функции, заданной табл. 3.7, при этом выполним последовательность действий, аналогичную той, которая была приведена в предыдущем примере.
На первом этапе запишем функцию в виде конъюнкции конституент нуля, соответствующих тем наборам, на которых функция принимает значение 0:
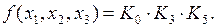
Далее, выразив конституенты нуля через дизъюнкции аргументов, получим искомую СКНФ:
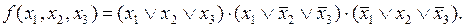
С помощью законов де Моргана СКНФ функции можно получить из СДНФ ее отрицания, записываемой по нулям. В качестве примера рассмотрим преобразование отрицания СДНФ функции, заданной табл. 3.7:
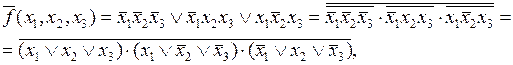
откуда, избавляясь от операции отрицания в начальной и конечной частях выражения, получим
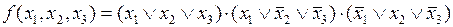 .
.
В СДНФ можно заменить операцию дизъюнкции операцией суммы по модулю 2. В том, что равенство при этом сохранится, можно убедиться путем сопоставления таблиц истинности получившихся выражений. Для рассмотренного выше примера:
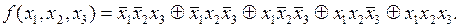
Такая форма называется совершенной полиномиальной нормальной формой (СПНФ).
Воспользуемся соотношением 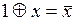 и заменим в СПНФ все переменные с отрицаниями на суммы вида
и заменим в СПНФ все переменные с отрицаниями на суммы вида 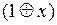 . После упрощения полученного выражения образуется канонический полином Жегалкина, который в общем виде можно записать следующим образом [4]:
. После упрощения полученного выражения образуется канонический полином Жегалкина, который в общем виде можно записать следующим образом [4]:
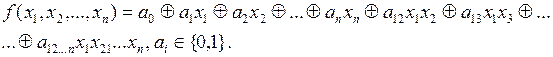
Для рассматриваемого примера:
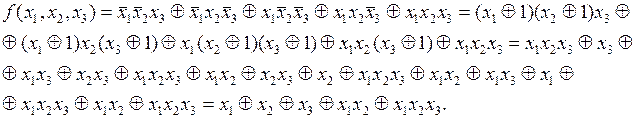
Дата добавления: 2014-12-27; просмотров: 1899;
