Кинетика гетерогенных химических реакций, сопровождающихся образованием твердого продукта реакции.

Если на поверхности реагирующего твердого вещества образуется твердый продукт реакции, кинетика реакции будет определяться характером этого покрытия.

В случае пористой пленки, она не будет оказывать сопротивление реагентам, подходящим к поверхности раздела, и слой продукта не будет влиять на скорость реакции. В случае непористой пленки, реагент должен будет диффундировать через этот защитный слой, пока не достигнет поверхности раздела. Кинетика такой реакции будет заметно отличаться.

Схема образования пористого Рисунок 23. Кинетика окисления продукта реакции. гладкой поверхности металлов:

1- непористый и 2 - пористый оксиды.

Сопротивление, вызванное диффузионным слоем, существует, как при непористом, так и при пористом продукте реакции, и оно может определять весь процесс. Если на поверхности образуется пористый продукт реакции и процесс контролируется диффузией через пограничный слой, скорость такого процесса будет выражаться уравнением:

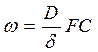(102)

Для сферических частиц:

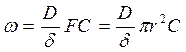(103)

В этом случае, хотя площадь поверхности раздела уменьшается со временем, эффективная площадь поверхности через которую происходит диффузия, остается постоянной.

Если продукт реакции непористый, то сопротивлением пограничного слоя можно пренебречь по сравнению с сопротивлением слоя продуктов реакции. Если толщина слоя продукта y, а M – масса твердого продукта реакции в момент времени t, то y = kM, где k – константа. Диффузия через слой твердого продукта будет выражаться уравнением:

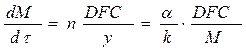(104)

где n – стехиометрический коэффициент.

В отдельном случае, когда С является постоянной величиной, т.е. когда осуществляется непрерывный подвод реагента :

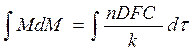(105)

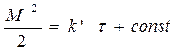(106)

Уравнение (106) обычно называют параболическим законом и было выведено Тамманом.

Рисунок 24. Окисление железа по параболическому закону: 1 – 975⁰С, 9 – 650⁰С.

Значение константы в вышеприведенном уравнении может быть рассчитано при t = 0, М = М₀. Тогда уравнение принимает вид:

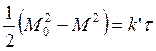(107)

В виде прореагировавшей доли a = 1 – М/М₀ параболическое уравнение может быть преобразовано:

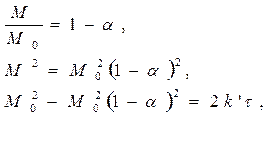
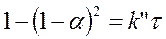(108)

Если твердое вещество имеет сферическую поверхность, выше приведенное решение неприменимо, поскольку F непрерывно уменьшается во время реакции. Было предложено несколько решений этой задачи: часть из них приближенные, часть точные.

Приближенное решение Яндера (1927г.)

Скорость роста продукта реакции обратно пропорционально его толщине:

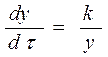, где y – толщина слоя продукта и k – константа пропорциональности.

Следовательно:

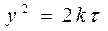(109)

Если r₀ – начальный радиус частицы, то прореагировавшая доля будет

;

; ;

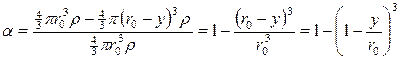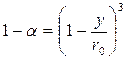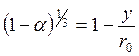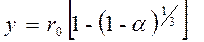(110)

Подставляя значение y в уравнение (109), получим

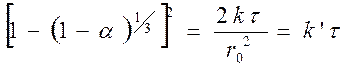(111)

График [1-(1-a)^1/3]² относительно времени даст прямую линию.

0,5

5 10 15 20

время , ч

Рисунок 25. Кинетика реакции 2Ni + O₂ = 2NiO по Яндеру:

1 – шарики 149 мкм, 1130⁰С; 2 – шарики 74 мкм, 1040⁰С.

Неточность уравнения (111) объясняется следующими причинами:

1. Уравнение составлено для плоской поверхности. Оно применимо, только для шара с большим радиусом по сравнению с толщиной слоя продукта.

2. Уравнение справедливо только тогда, когда объем непрореагировавшего ядра плюс объем продукта реакции равен объему первоначального материала. Это приблизительно соответствует действительности только на ранних стадиях реакции.

Упрощенная модель Кранка (1957), Гинстлинга и Броунштейна (1950).

r₀ r₁

r

Рисунок 26. Образование непористого слоя продуктов реакции:

r₀ – первоначальный радиус; C_i – концентрация на поверхности раздела фаз; 1 – непористый слой продукта; 2 – непрореагировавшее ядро.

Если I – число молей реагента диффундирующих за время t через слой продукта, то согласно закону Фика:

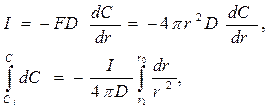
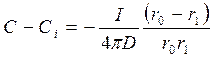(112)

Для процесса, контролируемого диффузией, C_i = 0, следовательно:

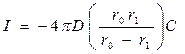(113)

Рассмотрим простой случай, когда С – постоянна.

Прореагировавшая доля

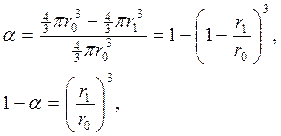
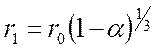(114)

Число молей непрореагировавшего твердого вещества, имеющегося в любой момент времени t, будет

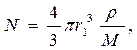где М – молекулярная масса реагирующего вещества; r - плотность реагирующего вещества.

Следовательно:

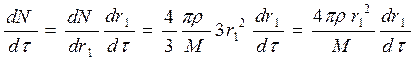(115)

Но скорость изменения N пропорциональна потоку реагента I, диффундирующего через сферическую оболочку толщиной r₀ – r₁.

Следовательно:

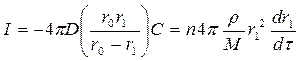, где n – стехиометрический коэффициент.

Поэтому

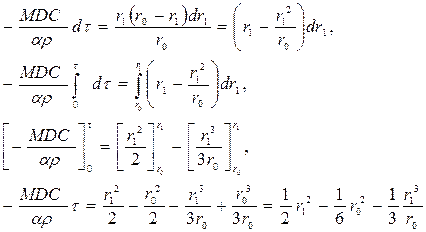
Выражая r₁ в виде a, получим:

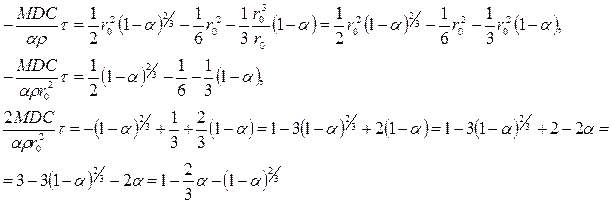
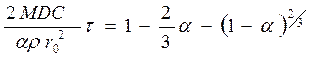(116)

Это означает, что графическая зависимость [1-2/3a-(1-a)^2/3] от времени будет представлена прямой линией.

1,0

[1-2/3a-(1-a)^2/3]

0,5

10 15 25

Рисунок 27. Кинетика реакции 2Ni + O₂ = 2NiO по Кранку – Гинстлингу – Броунштейну:

1 – d = 74 мкм, t = 1040⁰C; 2 – d = 149 мкм, t = 1130⁰C.

Уравнение (116) точнее чем уравнение Яндера, но веже оно справедливо для степени превращения вещества на 90%. Это объясняется тем, что не была принята во внимание поправка на изменение объема сферы во время реакции.