ЛЕКЦИЯ 9
Выведем зависимость между временем реагирования и радиусом невзаимодействующего ядра. Пусть дана не полностью прореагировавшая частица. Концентрация газа на поверхности непрореагировавшего ядра уменьшается при движении от периферии к центру. Однако скорость перемещения границы этого ядра в 1000 раз меньше, чем скорость движения газа к поверхностному слою непрореагировавшего ядра.
Скорость гетерогенного процесса в этом случае может быть приравнена к скорости диффузии через пористый слой твердых продуктов:
(80)
Поверхность S, к которой отнесена скорость процесса – это поверхность ядра с радиусом r при сферической форме частицы:
Итак примем на этапе интегрирования, скорость изменения размеров ядра (она определяется производной (dNUO3/dt)=(rUO3dVUO3/dt)) постоянна (квазистационарна) по отношению к скорости диффузии газа, определяемой градиентом концентраций dCH2/dr. Тогда уравнение (80) принимает вид:
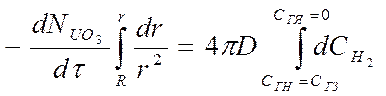(81)
Откуда
(82)
На втором этапе интегрирования будем считать, что размеры ядра изменяются. Так как в соответствии с уравнением (71)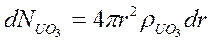 
, то уравнение (82) принимает вид:
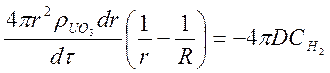(83)
Проинтегрируем это уравнение по времени от t = 0 (когда размер ядра равен размеру всей частицы, т.е. r = R до текущего времени t, при котором непрореагировавшее ядро имеет радиус r):
(84)
Если привести дроби в квадратных скобках к общему знаменателю и вынести за скобки R3, получим:
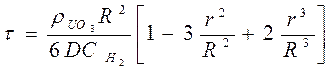(85)
С учетом соотношения (76)
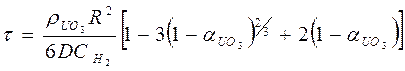(86)
При aUO3 = 1 уравнение (86) позволяет рассчитать время полного превращения твердой частицы tП при протекании гетерогенного процесса во внутреннедиффузионной области:
(87)
Итак, для внутреннедиффузионной области некаталитического гетерогенного процесса
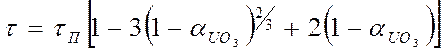(89)
Отсюда
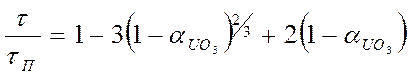(90)
График этого уравнения представлен на рисунке 18 – кривая 3.
Дата добавления: 2014-12-26; просмотров: 893;