ЛЕКЦИЯ 11.
Точное решение Валенси. (1935-1936гг.)
В приведенных нижет уравнениях используются следующие значения:
r0 – первоначальный радиус;
r1 – радиус непрореагировавшего ядра;
r2 – r1 – толщина слоя продукта;
I – число молей реагирующего вещества, диффундирующего за время t;
С – концентрация реагента;
Ci – концентрация реагента на поверхности раздела фаз;
W0 – первоначальная масса;
W – масса непрореагировавшего ядра;
rR – плотность реагирующего вещества;
rР – плотность продукта;
МR – молекулярная масса реагирующего вещества;
MP – молекулярная масса продукта;
N – число молей реагирующего вещества;
n – стехиометрический коэффициент;
VR – мольный объем реагирующего вещества;
VP – мольный объем продукта.
a (прореагировавшая доля) = (W0 –W)/W0 ; z = (1/n)(VP/VR).
r0
r1
r
r2
Рисунок 28. Образование непористых продуктов реакции.
Из закона диффузии Фика:
; 
; 
,
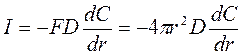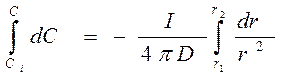
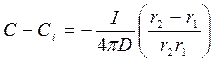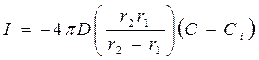Для процесса, контролируемого диффузией, Ci =0, следовательно:
.
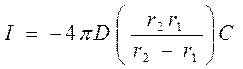Если количество реагента непрерывно пополнять, то С – величина постоянная.
Скорость изменения W пропорциональна I, потоку реагента, диффундирующего через сферическую оболочку толщиной r2 – r1:
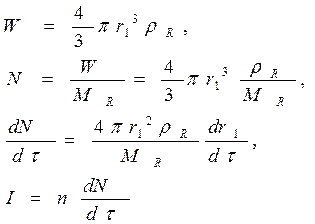
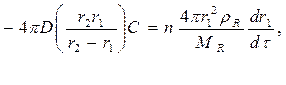
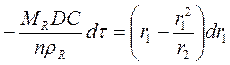(117)
Количество расходующихся молекул равно числу образующихся молекул, умноженному на стехиометрический коэффициент:
,
, 
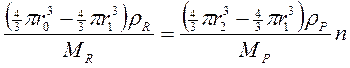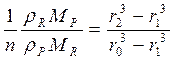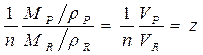
Следовательно:
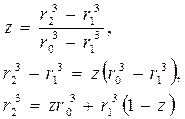
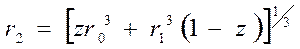(118)
Следует отметить, что если z =1, то r2=r0. Подставляем значение r2 из уравнения (118) в уравнение (117):
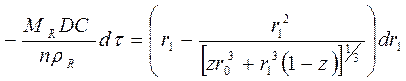(119)
Интегрируя уравнение (119) в пределах от r0 до r1 для t = 0 и t = t, получим
,
,
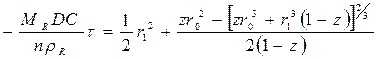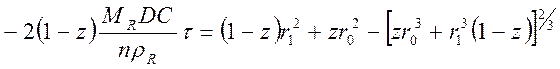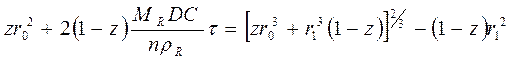(120)
, 
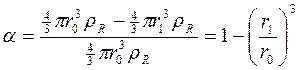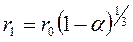. (121)
Подставляя значение r1 в виде a в уравнение (120), получим:
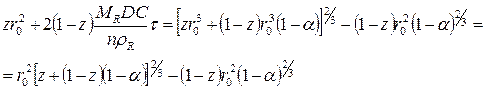(122)
Разделим уравнение (122) на r02
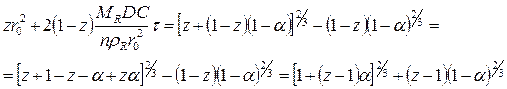(123)
График правой части уравнения (123) относительно t будет представлен прямой линией. Это уравнение справедливо до полного завершения реакции.
Если z = 1, уравнение Валенси упрощается
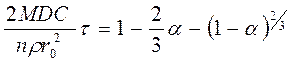(124)
Упрощенное уравнение (124) было выведено Кранком (1957) и Гинстлингом и Броунштейном (1950). Случай с цилиндрической формой образца был рассмотрен Картером (1963г.).
1,52
1,40
1,32
0 5 10 15 20 25
Время, ч
Рисунок 29. Кинетика реакции 2Ni + O2 = 2NiO по Валенси:
1 – d = 74 мкм, t = 10400C; 2 – d = 149 мкм, t = 11300C.
Итак, для реакций контролируемых диффузмей через непористый твердый продукт (реагирующее вещество имеет сферическую форму), существуют несколько уравнений:
1. Приближенное уравнение Яндера
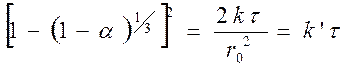
2. Уравнение Кранка – Гинстлинга – Броунштейна, хотя и не вполне точно, применимо в большинстве случаев
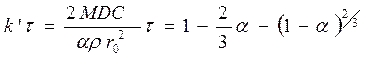
3. Уравнение Валенси точное
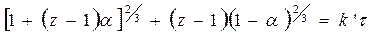
Для облегчения расчетов кинетических данных для любых значений прореагировавшей доли a графики функций :
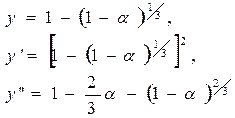
приведены на рисунке 30.
1,0
y
0,5
1
0 0,5 1,0
Прореагировавшая доля a
Рисунок 30. Графики различных кинетических уравнений:
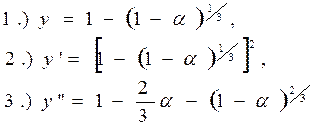
Дата добавления: 2014-12-26; просмотров: 1329;