Кинетические модели топохимических реакций.

Топохимические реакции – химические реакции, происходящие в твердой фазе, при которых процесс локализован на границе раздела твердое исходное вещество – твердый продукт реакции. Примеры топохимических реакций: дегидратация кристаллогидратов, окисление металлов, реакции процессов обжига, разложение взрывчатых веществ и др. название «топохимические» было предложено в 1918 г. Кольшуттером и в буквальном переводе означает: реакции, протекание которых связано с определенным местом в кристалле (от греческого «topoz» – место).

Основные черты топохимических реакций в значительной мере определяются тем, что реагирующие атомы, молекулы или ионы, образующие кристалл, жестко закреплены в узлах кристаллической решетки и лишены той подвижности, которой они обладают в газовой или жидкой фазах. Реакционная способность атомов или ионов в сильной степени зависит от того, в каком месте кристалла они находятся (в объеме, на поверхности грани, на ребре кристалла, на его вершине или на пороге дислокации). В связи с этим, при топохимических реакциях существенное значение приобретает реальная структура кристалла, связанная с наличием в кристалле различного рода дефектов, а образующийся при реакции твердый продукт, находясь в контакте с непрореагировавшим исходным веществом, может оказывать на скорость реакции каталитическое влияние, сила которого зависит от состояния продукта реакции. Благодаря тому, что при топохимических реакциях допустимо лишь минимальное перемещение реагирующих частиц, очень часто продукт реакции сохраняет внешнюю форму кристаллов исходного вещества.

Так как процесс локализован в пределах реакционной зоны, скорость процесса пропорциональна величине реакционной зоны в данным момент времени. Следовательно процесс лимитируется образованием центров кристаллизации (твердого продукта реакции).

Первоначально, как только центры реакции образовались, скорость реакции невелика, но по мере их роста, скорость – возрастает. Начиная с какого-то момента времени, зародыши начинают пересекаться. Момент их пересечения соответствует максимальной скорости. После пересечения площадь реакционной зоны начинает сокращаться, при этом уменьшается скорость.

a da/dt

а t б t

Рисунок 31. а – зависимость доли прореагировавшего вещества от времени; б – зависимость скорости реакции от времени.

На основании таких простых представлений о развитии топохимических реакций было выведено большое количество кинетических уравнений, наиболее простым из них является уравнение, предложенное Рогинским и Шульцем. Если число зародышей после того, как началась реакция, остается постоянным, скорость реакции должна быть пропорциональна реакционной поверхности S каждого зародыша.

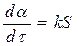(125)

Так как поверхность двумерна S = [l]², а объем (и следовательно масса, которая пропорциональна объему) трехмерен v = [l]³ , то выражая l через v и, соответственно, через степень прореагировавшего вещества a, получим:

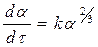(126)

Согласно этому уравнению, скорость реакции пропорциональна доли прореагировавшего вещества в степени 2/3, а общее количество прореагировавшего вещества пропорционально кубу времени.

Уравнение (126) было применено для анализа кинетических данных по термическому разложению твердых веществ. Процесс разложения азида кальция описывается на 40%, а a-азида свинца на 50%. Из самого смысла уравнения (126) следует, что оно может быть применено лишь в первой стадии реакции – до максимума скорости. После пересечения зародышей реакционная поверхность будет меньше, чем это следует из суммирования реакционных поверхностей отдельных зародышей, и поэтому начиная с этого момента, уравнение (126) будет давать завышенные значения скорости реакций.

Слияние реакционных поверхностей отдельных зародышей приводит к образованию общей реакционной поверхности, которая пропорциональна поверхности непрореагировавшей части кристалла. Выражая эту поверхность через массу непрореагировавшего вещества, получим следующее уравнение

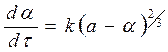, (127)

где а – масса непрореагировавшего вещества к моменту времени t.

Если, к примеру, в результате слияния зародышей образуется реакционная зона сферической формы, то скорость процесса хорошо описывается уравнением сокращающейся сферы

.

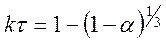Эти простые уравнения применяют при описании кинетики разложения многих веществ, однако экспериментально многие процессы не описываются этими уравнениями.

Существует целый класс реакций, для которых число зародышей N определяется уравнением

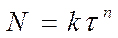(128)

где n – показатель степени, для быстрых экзотермических реакций n = 4-8 до 20. Он зависит от геометрической формы зародышей (куб, плоскость, сфера и т.д.).

Кинетика подобных реакций хорошо описывается обобщенным уравнением кинетики топохимических реакций выведенное Ерофеевым в 1946г.

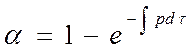(129)

где p – вероятность реагирования.

Позднее это уравнение приведено к наиболее известному в настоящее время виду топокинетического уравнения применительно к реакциям твердых веществ

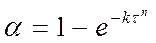(130)

Это уравнение известно как Уравнение Казеева – Ерофеева – Колмогорова.

По Ерофееву n – число последовательных стадий при образовании устойчивого начального центра новой фазы, плюс постоянное число, характеризующее форму зародыша, и равное 3 при образовании сферического зародыша, 2 – цилиндрического и 1 – плоского.

Из смысла уравнения следует, что сопоставление скоростей по константе скорости может быть сделано лишь в том случае, если n постоянно, что наблюдается далеко не всегда. По смыслу константа скорости должна иметь ту же размерность, что и константа скорости мономолекулярной реакции. В уравнении (130) постоянная k зависит от n.

В общем случае величина n отражает характер развития реакционной зоны. Во всех случаях. Когда n>1, исследуемый процесс находится в кинетической области. При n<1 процесс находится в диффузионной области.

Саковичем показано, что постоянная k из уравнения (130) не является еще константой скорости. Константа скорости может быть рассчитана по уравнению

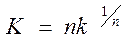(131)

Размерность константы скорости, находимой по этому уравнению, соответствует размерности константы мономолекулярной реакции.

Рассмотрим пример, когда уравнение (130) может быть применимо, для процессов, лимитируемых диффузией. В этом случае показатель n должен быть меньше единицы. Степень отклонения показателя n от единицы (1-n) Сакович определяет как меру погружения реакции в диффузионную область.

Итак, в дважды логарифмированном виде уравнение (130) представляет собой уравнение прямой lg[-lg(1-a)]=nlgt+lgk+lglge. Откладывая по оси абсцисс значения lgt, а по оси ординат значения lg[-lg(1-a)], мы должны получить прямую линию, если наши экспериментальные результаты описываются уравнением (130). В качестве примера приводим кинетический анализ экспериментальных данных по скорости дегидратации пентагидрата сульфата меди. Откладывая значения lgt по оси абсцисс, а значения lg[-lg(1-a)] по оси ординат, видим, что экспериментальные точки ложаться на прямую линию, рис 32. Находя из графика тангенс угла наклона этой прямой к оси абсцисс, получаем значение n = 1,88.

lgt 1,0 2,0

0

-1,0

lgk a

tga = n

-2,0

Рисунок 32. Кинетический анализ экспериментальных данных по уравнению Казеева – Ерофеева – Колмогорова.

Значение lgk может быть найдено из того же графика. Для этого продолжаем прямую до пересечения с осью ординат, находим значение lg[-lg(1-a)] в точке пересечения – 2,56. Поскольку в нашем расчете мы оперируем не натуральными логарифмами, а десятичными, вычитая из него -lglge = -0,36, получаем для lgk = - 2,20.

Как уже указывалось выше, для того чтобы найти константу скорости, нужно значение k из топокинетического уравнения (130) подставить в выражение (131), предложенное Саковичем, или в логарифмической форме

.

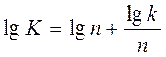Подставив в это уравнение lgn, n и lgk, значения которых нам известны, найдем

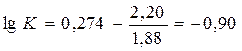и К = 0,126.