Разомкнутая, произвольно разветвленная сеть

Исходными данными для расчета, как и во всех предыдущих сетях, являются токи нагрузок I_kH, длины участков l_k и допустимые потери напряжений от источника до всех потребителей. Расчет таких сетей хотя и громоздок, но в конечном счете сводится к применению ранее изложенных методов расчета разомкнутых сетей.

На рисунке представлена разомкнутая, произвольно разветвленная сеть и последовательность ее расчета, которая сводится к следующему:

1. Выбирается одно из направлений за магистральное (например, ABCDEFG), сосредоточив все нагрузки в точках этой магистрали

Критерием для выбора магистрального направления может быть или максимально допустимая потеря напряжения или максимум суммы произведений токов на участках на длину участков ( 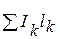) для выбранного направления.

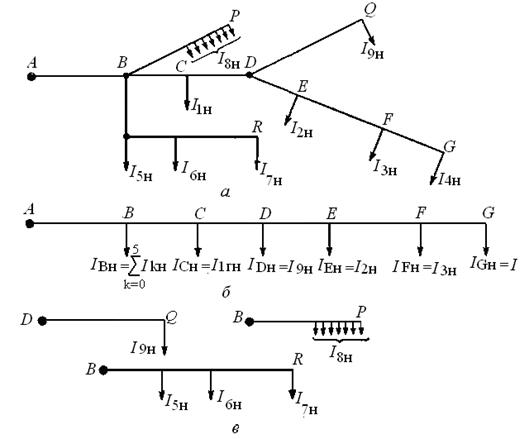
Рис 4.10. Разомкнутая, произвольно разветвленная сеть.

а – исходная сеть, б – расчетная сеть по магистральному направлению, в – расчетные сети разветвлений

2. Полученная разомкнутая сеть с несколькими сосредоточенными нагрузками (см. рис) рассчитывается тремя методами (Sk = const, jk = const и V = V_mln) и выбираются оптимальные сечения участков магистрали S_AB, S_BС, S_CD, S_DE, S_EF и S_FG.

3. Подсчитывается потеря напряжения на участках магистрали от питательного пункта А до точек приложения сосредоточенных нагрузок ΔU_AB, ΔU_AС, ΔU_AD, ΔU_AE, ΔU_AF.

4. Определяется допустимая потеря напряжения на разветвлениях относительно выбранной магистрали

ΔU_DQ = ΔU_AQ(доп) - ΔU_{АD ,}

ΔU_BP = ΔU_AP(доп) - ΔU_АB ,

ΔU_BR = ΔU_AP(доп) - ΔU_АB.

5. Рассчитываются сечения участков разветвлений (рис. 4. 12) по законам расчета отдельных разомкнутых сетей с известными допустимыми потерями напряжений.

Рис 4. 11. К расчету сечений проводов

6. Проверяется, чтобы при выбранных сечениях Sk потери напряжения во всех направлениях исходной сети были не более допустимых значений.

В общем случае подобный расчет следует произвести для двух-трех магистральных направлений и затем выбрать оптимальный с точки зрения получения минимума веса и максимума эластично­сти сети.