В изолированных системах самопроизвольно могут со­вершаться только такие необратимые процессы, при которых энтропия системы возрастает (DS > 0).

Для неизолированных систем нужно учитывать не только изменение энтропии, но и изменение энергии. Поэтому необхо­димо рассматривать две тенденции, определяющие направление самопроизвольно протекающих процессов:

- стремление системы к достижению минимума энергии;

- стремление системы к максимуму энтропии, то есть к неупорядоченности.

Процессы, при которых энергия в неизолированной системе уменьшается, а энтропия возрастает, протекают самопроизвольно. Самопроиз­вольность других процессов зависит от того, какая из этих двух тенденций – энергетическая или энтропийная – окажется более эффективной, какая из этих противоборствующих тенденций получит перевес над другой. В этом проявляется противоречи­вость материального мира.

Для однозначной формулировки условий протекания само­произвольных процессов в любых системах введена ещё одна термодинамическая функция, которая характеризует одновременно и энергетику, и неупорядоченность систем. Впервые такую термодинамическую функцию ввёл Д. У. Гиббс, и в память об этом выдающемся американском учё­ном её назвали энергией Гиббса (G).

Джозайя Уиллард Гиббс (11.11 1839–28. IV 1903). Американский физик и физико-химик, член Национальной АН США (с 1879). Родился 11 февраля в Нью-Хейвене. Окончил Йельский университет (1858; доктор философии, 1863). В 1863–1866 преподавал в Йельском колледже. Совершенствовал образование в Сорбонне и Коллеж де Франс в Париже (1866–1867), в Берлин­ском (1867) и Гейдельбергском (1868) университетах. С 1871 – профессор Йельского университета. Один из основоположников тер­модинамики.

Предложил (1873) графические модели описания тер­модинамических свойств вещества. Разработал (1875–1878) теорию термодинамических потенциалов Изучил (1875) условия равнове­сия гетерогенных систем. Вывел (1875–1878) правило фаз, соглас­но которому в равновесной гетеро­генной системе число фаз не мо­жет превышать числа компонен­тов системы, увеличенного на два. Предложил (1878) графическое изображение состояния трехкомпонентной системы (треугольник Гиббса). Заложил основы термо­динамики поверхностных явлений и электрохимических процессов; ввёл понятие адсорбции. Дал (1902) атомистическое истолкова­ние развитым им термодинамиче­ским методам. Осуществил иссле­дования в области векторного ана­лиза и алгебры кратных чисел, электромагнитной и механической теорий света.

Член многих академий наук и научных обществ. Член Американской академии искусств и наук (с 1880).

Биохимические процессы обычно происхо­дят при изобарно-изотермических условиях. В этих условиях энергетическое состояние системы характеризуется энтальпией, а мерой неупорядоченности системы будет произведение её эн­тропии и температуры. Функцией, учитывающей обе эти ха­рактеристики и противоположность в тенденции их изменения при самопроизвольных процессах, является энергия Гиббса:

G = Н -TS.

Энергия Гиббса является обобщённой термодинамической функцией состояния системы, учитывающей энергетику и неупорядоченность системы, при изобарно-изотермичес­ких условиях.

Энергию Гиббса называют также изобарно-изотермическим потенциаломили свободной энергией.

Подобно другим термодинамическим параметрам и функ­циям, характеризующим состояние системы, изменение энер­гии Гиббса в результате любого процесса определяется только конечным и начальным состоянием системы, независимо от пу­ти процесса:

DG = G_кон - G_нач

Для полной энергетической характеристики вещества при стандартных условиях используют стандартную энергию Гиббса образования вещества DG^о, значение которой дано в справочной литературе. Для простых веществ в термодинамически устой­чивой форме стандартная энергия Гиббса их образования ус­ловно принята равной нулю.

Изменение энергии Гиббса в результате химической реак­ции при стандартных условиях вычисляют по уравнению:

DG_р = ∑v_кон DG_кон (Y_кон) - ∑v_исх DG_исх (X_исх),

где DG_j(Y_j), DG_i(X_i) - стандартные энергии Гиббса продуктов реакции Y_j и исходных веществ X_i;

v_кон. и v_нач - соответствующие стехиометрические коэффициенты в уравнении химической реакции.

Изменение энергии Гиббса для биохимических процессов при условиях, отличных от стандартных, рассчитывают на основе экспериментальных значений DН и DS для этих процессов по уравнению:

DG = DН - TDS,

где DН - характеризует полное изменение энергии системы при р, Т = const и отражает стремление системы к минимуму энергии;

TDS - характеризует ту часть энергии, которую нельзя превратить в работу, и отражает стремление системы к максимуму неупорядоченности;

DG - характеризует ту часть энергии, которую можно превратить в работу, и является термодинамическим критерием возможности самопроиз­вольного протекания любых процессов при р, Т = const.

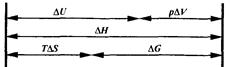
Соотношение между из­менениями важнейших термо­ди-намических параметров и функций состояний системы, описывающими химические и биохимические процессы при р, Т = const, представлено в таблице и на следующей схеме.

Второй закон термодинамики систем формули­руется следующим образом: В системе при постоянных температуре и давлении са­мопроизвольно могут совершаться только такие процес­сы, в результате которых энергия Гиббса уменьшается (DG_кон < DG_нач или DG < 0).