Нагрузкой
Пусть нагрузка равномерно распределяется на части линии. На рис. 4. 7 показаны такая линия, график распределения тока Iн и потери напряжения ∆U вдоль линии.
Потеря напряжения в линии складывается из двух составляющих
∆Ua2 = ∆Ua1 + ∆U12
Очевидно, при постоянном сечении линии S = const потеря напряжения на участке a1 равна
∆Ua1 = IHra1 = IHL1/γS.
Потеря напряжения ца участке 1 – 2 с распределенной нагрузкой находится так:
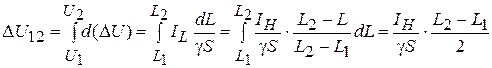 .
.
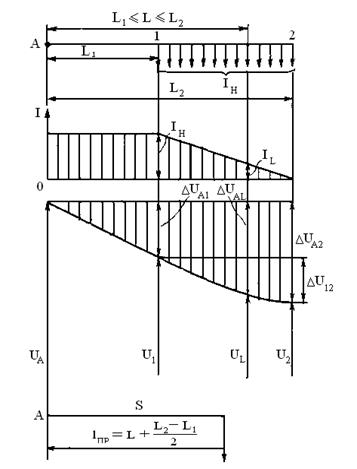
Рис. 4.7. Простая разомкнутая сеть с равномерно распределенной нагрузкой.
Iн- суммарный ток нагрузки; IL- ток в сечении L; ∆UА2- потеря напряжения в сети; ∆UА1, ∆UАL, ∆U12- потеря напряжения на соответствующих участках сети.
Из уравнений находим сечение провода
S = IHlпр/γ∆Uдоп .
Приведенная длина линии lпр при равномерной нагрузке:
lпр= L1 + (L2 - L1)/2.
Таким образом, линия с равномерно распределенной суммарной нагрузкой IH эквивалентна линии с сосредоточенной нагрузкой IH, приложенной к середине загруженного участка линии. Если нагрузка равномерно распределена вдоль всей линии (l1 = o), то приведенная длина определяется как lпр=0,5L2; если при этом налицо некоторая неравномерность распределения нагрузки, то lпр = (0,4 ÷ 0,6) L2, причем 0,4 соответствует большей нагрузке в конце линии, а 0,6 – в начале линии.
3. Разомкнутая сеть с несколькими сосредоточенными нагрузками (рис. 4.8).
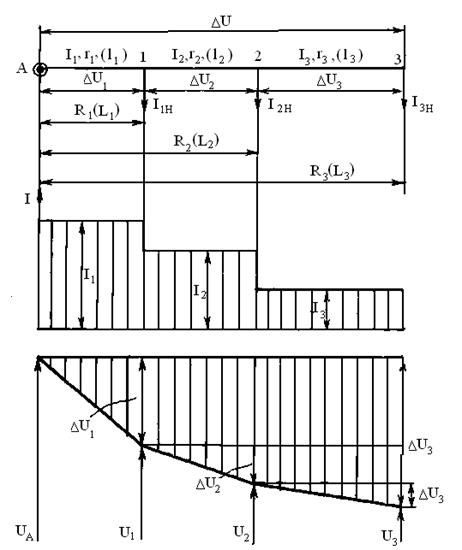
Рис. 4.8. Разомкнутая цепь с несколькими сосредоточенными нагрузками:
∆U- потеря напряжения в сети; ∆U1, ∆U2… ∆U k- потеря напряжения на участках; I1,I2…Ik- токи на участках; r1(l1), r2(l2)…rk(lk)- сопротивления(длины) участков; R1(L1), R2(L2)… Rk(Lk)- сопротивления(длины) частей линии от источника А до приложения соответствующего тока нагрузки; I1н, I2н… Ikн- токи нагрузок
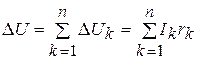 ,
,
где Ik – сила токов,
Rk – сопротивление,
Lk – длина,
ΔUk – падение напряжения,
Ikn – токи нагрузки потребителей,
Rka – сопротивления участков сети,
Lka – длины от питательного пункта А до точки приложения k - ой нагрузки.Потери напряжения в сети
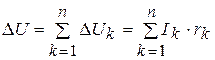 (4. 12)
(4. 12)
при n сосредоточенных нагрузках

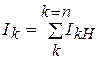
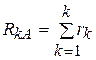 от А до К нагрузки (4. 13)
от А до К нагрузки (4. 13)
Из (4. 12) и (4. 13) уравнение потери напряжения в сети с n неизвестными сечениями участков Sк
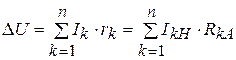 (4. 14)
(4. 14)
Дополнительные условия Sk = const, jk = const, вес сети V = Vmin
 Первый вид расчета: S = Sk = const
Первый вид расчета: S = Sk = const
Выражение (4. 14) можно записать в двух видах:
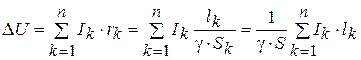 (4. 15)
(4. 15)
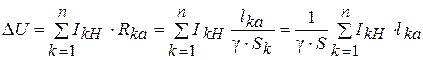 (4. 16)
(4. 16)
Введем понятие – суммарный момент токов относительно пункта А из (4. 15) и (4. 16)
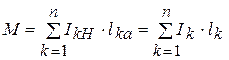 (4. 17)
(4. 17)
Искомое сечение сети S = M/γUдоп
Удельное сопротивление меди при температуре То = 15 оС –
0.0175, Ом мм2 /м; при температуре Т – 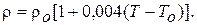
Второй вид расчета: 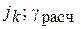 – const.
– const.
Запишем (4. 14) в виде:
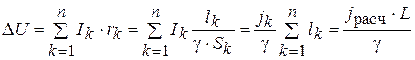 . (4. 18)
. (4. 18)
Из (4.18) jрасч = γΔUдоп/L,
где L – длина линии с допустимой потерей напряжения
ΔUдоп.– допустимые потери напряжения в линии.
Тогда Sk = Ik / jрасч .
Третий вид расчета: расчет на минимум веса сети. V = Vmin
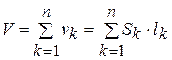 (4. 19)
(4. 19)
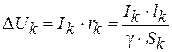 (4. 20)
(4. 20)
Sk = Iklk/γ ΔUk
из (4. 19) и (4. 20) имеем
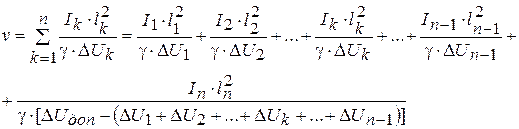 (4. 21)
(4. 21)
Найдем минимум функции U = U(ΔU1 ΔU2... ΔUk…… ΔUn-1).
Из уравнения (4. 21) получим
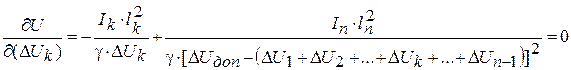 . (4. 22)
. (4. 22)
Из (4. 22) с учетом (4. 21) 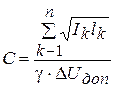 (4. 23)
(4. 23)
и 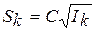 (4. 24)
(4. 24)
Пример:Дана сеть с несколькими сосредоточенными нагрузками (рис. 4. 9). Рассчитать тремя методами объем проводов.
На 4. 9 введены обозначения: vS – объем меди сети при расчете на постоянство сечения; vj – объем меди при расчете на постоянство плотности тока; vmin – минимум меди сети при заданной потере напряжения; S1, S2-– сечения участков сети.
1) S1 = S2 = S S1/S2 = 1
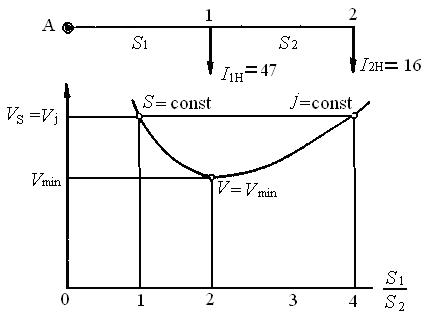
Рис. 4.9. График сравнения трех видов расчета сети с несколькими сосредоточенными нагрузками
2) 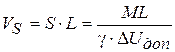 (4. 25)
(4. 25)
3) 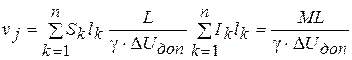
При любом способе расчета данной сети наиболее нагруженным в тепловом отношении является головной участок, который в первую очередь проверяется по допустимому нагреву. Нетрудно показать, что наиболее рациональное распределение меди между участками с точки зрения нагрева получается при расчете на постоянство плотности тока.
В общем случае расчет разомкнутой сети с несколькими сосредоточенными нагрузками надо вести всеми тремя способами, выбирая каждый раз ближайшие стандартные сечения участков (для головного участка и рядом лежащих – ближайшие большие, для концевых – ближайшие меньшие).
После этого надо проверить реальную потерю напряжения и нагрева, затем путем сравнения трех фактических вариантов расчета выбрать оптимальный.
Дата добавления: 2014-12-24; просмотров: 1235;
