Энтропия. Большинство процессов представляет собой два одновременно происходящих явления: передачу энергии и изменение в упорядоченности расположения частиц друг

Большинство процессов представляет собой два одновременно происходящих явления: передачу энергии и изменение в упорядоченности расположения частиц друг относительно друга.

Частицам (молекулам, атомам, ионам) присуще стремление к беспорядочному движению, поэтому система стремится перейти из более упорядоченного состояния в менее упорядоченное. Количественной мерой беспорядка является энтропия S. Изменение энтропии ΔS в изолированной системе, переходящей из состояния 1 в состояние 2, можно определить соотношением

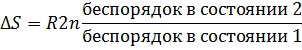
где R- газовая постоянная.

Если, например, баллон с газом соединить с вакуумированным сосудом, то газ из баллона будет распределяться по всему объёму сосуда. При этом система из более упорядоченного состояния (с меньшим беспорядком) переходит в состояние менее упорядоченное (с большим беспорядком). Таким образом, при переходе системы из более упорядоченного состояния в менее упорядоченное состояние энтропия возрастает.

Переход же системы из менее упорядоченного состояния в более упорядоченное состояние связан с уменьшением энтропии, и самопроизвольное протекание подобного процесса менее вероятно. Так, ясно, что в рассматриваемом примере система самопроизвольно не может перейти из состояния 2 в состояние 1, т.е. невероятно, чтобы газ сам собой собрался в баллоне. В случае перехода системы из менее упорядоченного состояния в более упорядоченное ΔS системы - величина отрицательная, т.е. энтропия S системы уменьшается.

Энтропия возрастает при переходе жидкости в пар, при растворении кристаллического вещества и т.д. В процессах конденсации и кристаллизации вещества энтропия уменьшается. Энтропия вещества в газовом состоянии значительно больше, чем в жидком, а тем более, чем в твердом.

Энтропии веществ, как и их теплоты образования, принято относить к определенным условиям, обычно при температуре 25 ⁰С (298 К) и давлении 1 атм. Энтропию при этих условиях обозначают S⁰₂₉₈ и называют стандартной энтропией.

Значениями энтропии веществ пользуются для установления изменения энтропии системы в результате соответствующих процессов. Так, для химической реакции

аА+bB+…= dD+еЕ+…изменение энтропии системы будет

ΔS= (dS_D + eS_E+…)-( aS_A + bS_B+...) или ΔS= ∑S_прод. - ∑S_исх.

Об изменении энтропии в химических реакциях можно судить по изменению объёма системы в ходе реакции. Например, в реакции ½ С (графит)+½ СО₂(г)=СО(г) наблюдается увеличение объёма ΔV>0; следовательно, энтропия возрастает ΔS> 0 (ΔS⁰₂₉₈=87,7 дж/моль∙град). В случае же реакции образования Н₃N из водорода и азота 3/2 Н₂ (г)+1/2 N₂ (г)= H₃N(г) наоборот, объём системы уменьшается ΔV<0; следовательно, энтропия уменьшается ΔS<0 (ΔS⁰₂₉₈=99,1дж/моль∙град).

Если же реакция протекает между твердыми веществами, например,

Аl(к)+Sb(к)=АlSb(к), то изменения объёма системы и её энтропии практически не происходит (ΔS⁰₂₉₈=4,03дж/моль∙град). То же самое относится и к процессам, в которых число молей газообразных веществ не изменяется, например, С (графит)+ О₂ (г)= СО₂ (г), ΔS=2,9дж/моль∙град.

4.1.3. Энергия Гиббса и направленность химических процессов

Возможность самопроизвольного протекания химического процесса определяется двумя факторами: стремлением системы к понижению внутренней энергии за счет экзотермической реакции (-∆H) и стремлением системы к увеличению неупорядоченности в расположении частиц за счет теплового движения, мерой которой является функция состояния, называемая энтропией S.

Если ∆H незначительно зависит от температуры, то энтропия с повышением температуры сильно возрастает. Влияние как энтальпийного так и энтропийного факторов учитывается в уравнении ∆G=∆H-T∆S. Функцию G называют энергией Гиббса, она является мерой устойчивости системы в условиях T=const и p=const.

Состояние системы при постоянном объеме описывается функцией, которую называют энергией Гельмгольца: ∆P=∆U-T∆S. Таким образом, ∆G отличается от ∆P так же, как ∆H от ∆U на величину, равную работе расширения p∆V.

Изменение энергии Гиббса ∆G определяет возможность или невозможность самопроизвольного протекания процесса. Если ∆G<0, т.е. по ходу реакции происходит уменьшение энергии Гиббса, то этот процесс термодинамически возможен. Если ∆G>0, т.е. процесс ведет к увеличению энергии Гиббса, то такая реакция термодинамически невозможна. Если ∆G=0, то реакционная система находится в состоянии равновесия.

При положительном значении ∆S и, следовательно, T∆S величина G будет отрицательной: а) при любых отрицательных значениях Н, т.е. все экзотермические процессы в этом случае возможны; б) при положительных значениях ∆Н, но при условии, что по абсолютному значению ∆Н<T∆S, т.е. эндотермические реакции возможны, когда энтропийный фактор преобладает над энтальпийным, что легче реализуется с ростом температуры.

При отрицательном значении ∆S в уравнении ∆G=∆H-T∆S величина T∆S становится положительной, поэтому в этом случае эндотермические реакции (+∆Н) самостоятельно протекать не могут, так как ∆G будет величиной также положительной. Из экзотермических реакций (-∆Н) при таком условии возможны только те, которые характеризуются большим отрицательным значением ∆Н, т.е. те эндотермические реакции, для которых сумма -∆Н+(-Т∆S) имеет отрицательное значение.

При очень низких температурах величина Т∆S минимальна, так как и энтропия в этих условиях изменяется незначительно, поэтому преимущественное влияние на направление процесса имеет энтальпийный фактор и обычно процессы идут в сторону экзотермических реакций. В конденсированных системах реакции протекают с незначительным изменением энтропии, поэтому знак ∆G определяется знаком ∆Н.

Таким образом, для определения возможности протекания процесса при данных условиях надо найти знак ∆G. С этой целью в справочных таблицах находят стандартные значения ∆Н и S для веществ, участвующих в реакции, по которым вычисляют ∆G на формулы ∆G^o₂₉₈=∆H ^o₂₉₈-T∆S ^o₂₉₈ [3].

Пример 1. Расчет теплового эффекта химической реакции по теплоте образования реагирующих веществ и продуктов реакции.

Определите количество теплоты, выделяющейся при гашении 100кг извести водой при 25^оС, если известны стандартные теплоты образования веществ, участвующих в химической реакции:

∆H ^o₂₉₈, CaO(к) = -635,1 кДж∙моль^-1;

∆H ^o₂₉₈, H₂O(ж) = -285,84 кДж∙моль^-1;

∆H ^o₂₉₈, Ca(OН)₂(к) = -986,2 кДж∙моль^-1.

Решение. Реакция гашения извести: СаО(к)+Н₂О(ж)=Са(ОН)₂(к). Согласно первому следствию из закона Гесса тепловой эффект химической реакции равен разности между суммой теплот образования реагирующих веществ с учетом стехиометрических коэффициентов:

=

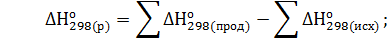
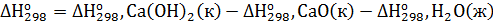=-986,2-(-635,1)-(-285,84) = 65,26 кДж∙моль^-1

Таким образом, при гашении водой 1 моль извести выделяется 65,26кДж, при гашении 1кмоль извести – 65260 кДж. М(СаО) = 56г∙моль^-1=56кг∙моль-¹; m(СаО) = 100кг;

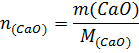
При гашении водой 100 кг извести выделяется 100/56∙65260=116536кДж.

Пример 2. Расчет теплоты образования.

Определить теплоту образования Са(ОН)₂тв на основе реакций:

СаСО₃→СаО+СО₂+∆Н₁; СаО+Н₂О→Са(ОН)₂тв+∆Н₂.

Решение. Для определения суммарной теплоты образования ∆Н для этой реакции определяем ∆Н₁ и ∆Н₂, тогда ∆Н=∆Н₁+∆Н₂;

∆Н₁=∆Н_СаО+∆Н_(СО2)-∆Н_СаСО3 = +177,83 кДж∙моль^-1;

∆Н₂=∆Н_Са(ОН)2-∆Н_СаО-∆Н_Н2О = -65,2 кДж∙моль^-1;

∆Н= +177,83 – 65,2 = +113,61 кДж∙моль^-1.

Пример 3. Рассчитайте тепловой эффект реакции горения сероводорода по следующим данным: Н₂S_(г) + 3/2O₂=Н₂О_(ж) + SО₂(г)

1)S_(к) + Н₂ = Н₂S_(г); ∆Н₁= -20,17 кДж

2)Н₂ + 1/2 O₂ = H₂O(ж); ∆Н₂= -286,0 кДж

3)S_(к) + О₂ = SО₂(г); ∆Н₃= -297 кДж

Решение. Уравнение 1-3 есть термохимические уравнения образования соответственно 1 моль Н2S(г), Н2О(ж), SО2(г) из простых веществ в стандартных условиях: Т=298К и Р=101,325 кПа, а тепловые эффекты – стандартные энтальпии образования указанных соединений ∆H ^o_298. Если сложить термохимические уравнения 2 и 3 и вычесть уравнение 1, получим искомое уравнение

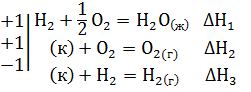
Н₂S_(г) + 3/2 O₂ = H₂O_(ж) + SO_2(г) ∆Н=∆Н₁+∆Н₂-∆Н₃

Подставить численное значение энтальпий образования Н₂S_(г) , Н₂О_(ж), SO_2(г), получим значение теплового эффекта реакции ∆Н= -286 -297 –(-20,17) = = -562,8 кДж. Отрицательное значение энтальпии реакции горения сероводорода означает, что данная реакция экзотермическая.

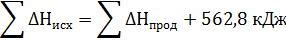
Тепловой эффект можно включить в уравнение химической реакции.

Н₂S_(г) + 3/2О₂ = Н₂О_(ж) + SO_2(г) + 562,8 кДж. Эта запись также представляет собой термохимическое уравнение реакции.

Пример 4. Определение изменения энтропии в стандартных условиях. Определить изменение энтропии реакции Na₂O+SiO₂=Na₂SiO₃ при температуре 298К.

Решение. Находим по справочнику значения энтропии продукта и исходных веществ при Т=298К, S ^o_298, Na₂O(т)=42,09Дж∙моль^-1∙к^-1:

S ^o_298, SiO₂ (т) = 71,1Дж∙моль^-1∙к^-1;

S ^o_298, Na₂SiO₃ (т)=113,8Дж∙моль^-1∙к^-1. Изменение энтропии в химической реакции равно разности между суммой энтропий продуктов реакции и суммой энтропий исходных веществ с учетом стехиометрических коэффициентов.

S^o_{298 х.р.} = S^o_298, Na₂SiO₃(т) – S^o_298, SiO₂ (т) - S^o_298, Na₂O_(т) = 113,8-71,1-42,09=0,61 Дж∙моль^-1∙к^-1

Пример 5. Определение изменения энтропии при фазовых превращениях. Определить изменение энтропии 1г кристобалита при температуре плавления 1986К, если теплота обратного фазового превращения кристобалита равна 744,05 Дж∙r^-1.

Решение. Изменение энтропии при переходе вещества из одного агрегатного состояния в другое равно: , где ∆Н-теплота обратимого фазового превращения.

S₂-S₁=∆S= 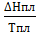= = 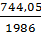0,238Дж∙г^-1∙град^-1.

Пример 6.Вычислите 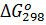для химической реакции 2SO₂(г)+О₂(г)↔2SO₃(г). В каком направлении может протекать эта реакция в стандартных условиях?

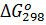, SO₂(г) = -300,37 кДж∙моль^-1;

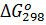, SO₃(г) = -370,37 кДж∙моль^-1

Решение. Изменение энергии Гиббса в химической реакции

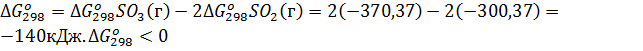, поэтому в стандартных условиях данная реакция может протекать в сторону образования SO₃.