Методы выявления основной тенденции (тренда) в рядах динамики
Одна из основных задач изучения рядов динамики – выявить основную тенденцию (закономерность) в изменении уровней ряда, именуемую трендом. Закономерность в изменении уровней ряда в одних случаях проявляется наглядно, в других – может маскироваться колебаниями случайного или неслучайного характера. Поэтому, чтобы сделать правильные выводы о закономерностях развития того или иного показателя, надо суметь отделить тренд от колебаний, вызванных случайными кратковременными причинами. На основании выделенного тренда можно экстраполировать (прогнозировать) развитие явления в будущем. С этой целью (устранить колебания, вызванные случайными причинами) ряды динамики подвергают обработке.
Существует несколько методов обработки рядов динамики, помогающих выявить основную тенденцию изменения уровней ряда, а именно: метод укрупнения интервалов, метод скользящей средней и аналитическое выравнивание. Во всех методах вместо фактических уровней при обработке ряда рассчитываются иные (расчетные) уровни, в которых тем или иным способом взаимопогашается действие случайных факторов и тем самым уменьшается колеблемость уровней. Последние в результате становятся как бы «выравненными», «сглаженными» по отношению к исходным фактическим данным. Такие методы обработки рядов динамики называются сглаживанием или выравниванием рядов динамики.
Простейший метод сглаживания уровней ряда – укрупнения интервалов, для определяется итоговое значение или средняя величина исследуемого показателя. Этот метод особенно эффективен, если первоначальные уровни ряда относятся к коротким промежуткам времени. Например, если имеются данные о ежесуточном производстве мороженого на предприятии за месяц, то, естественно, в таком ряду возможны значительные колебания уровней, так как чем меньше период, за который приводятся данные, тем больше влияние случайных факторов. Чтобы устранить это влияние, рекомендуется укрупнить интервалы времени, например до 5 или 10 дней, и для этих укрупненных интервалов рассчитать общий или среднесуточный объем производства (соответственно по пятидневкам или декадам). В ряду с укрупненными интервалами времени закономерность изменения уровней будет более наглядной.
По своей сути метод скользящей средней похож на метод укрупнения интервалов, но в данном случае фактические уровни заменяются средними уровнями, рассчитанными для последовательно подвижных (скользящих) укрупненных интервалов, охватывающих m уровней ряда. Например, если принять m=3, то сначала рассчитывается средняя величина из первых трех уровней, затем находится средняя величина из 2-го, 3-го и 4-го уровней, потом из 3-го, 4-го и 5-го и т.д., т.е. каждый раз в сумме трех уровней появляется новый уровень, а два остаются прежними, что и обусловливает взаимопогашение случайных колебаний в средних уровнях. Рассчитанные из m членов скользящие средние относятся к середине (центру) каждого рассматриваемого интервала.
Сглаживание методом скользящей средней можно проводить по любому числу членов m, но удобнее, если m – нечетное число, так как в этом случае скользящая средняя сразу относится к конкретной временнОй точке – середине (центру) интервала. Если же m – четное, то скользящая средняя относится к промежутку между временнЫми точками: например, при сглаживании по четырем членам (m=4) средняя из первых четырех уровней будет находиться между второй и третьей временной точкой, следующая – между третьей и четвертой и т.д. Тогда, чтобы сглаженные уровни относились непосредственно к конкретным временнЫм точкам, из каждой пары смежных промежуточных значений скользящих средних находят среднюю арифметическую, которую относят к временной точке, находящейся между смежными. Такой прием двойного расчета сглаженных уровней называется центрированием.
Недостатком метода скользящей средней является то, что сглаженный ряд укорачивается по сравнению с фактическим с двух концов: при нечетном m на (m-1)/2, а при четном m – на m/2 с каждого конца. Применяя этот метод, надо помнить, что он сглаживает (устраняет) лишь случайные колебания. Если же, например, ряд содержит сезонную волну (см. 6.6), она сохранится и после сглаживания методом скользящей средней. Кроме того, этот метод сглаживания, как и метод укрупнения интервалов не позволяет выражать общую тенденцию изменения уровней в виде математической модели.
Наиболее совершенным методом обработки рядов динамики в целях устранения случайных колебаний и выявления тренда является выравнивание уровней ряда по аналитическим формулам (или аналитическое выравнивание). Суть аналитического выравнивания заключается в замене эмпирических (фактических, исходных) уровней yi теоретическими 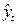 , которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени:
, которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: 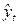 = f(t).
= f(t).
При этом каждый фактический уровень yi рассматривается обычно как сумма двух составляющих:
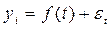 , (64)
, (64)
где f(t) = 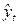 - систематическая составляющая, отражающая тренд и выраженная определенным уравнением;
- систематическая составляющая, отражающая тренд и выраженная определенным уравнением; 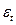 - случайная величина, вызывающая колебания уровней вокруг тренда.
- случайная величина, вызывающая колебания уровней вокруг тренда.
Задача аналитического выравнивания сводится к следующему:
1) определение на основе фактических данных формы (вида) гипотетической функции 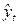 = f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя;
= f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя;
2) нахождение по эмпирическим данным параметров указанной функции (уравнения);
3) расчет по найденному уравнению теоретических (выравненных) уровней.
В аналитическом выравнивании наиболее часто используются простейшие функции, представленные в табл. 15, где обозначено 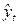 - теоретические (выравненные) уровни (читается как «игрек, выравненный по t»); t – условное обозначение времени (1, 2, 3 …); a0, a1, a2, ... – параметры аналитической функции; k – число гармоник (при выравнивании по ряду Фурье).
- теоретические (выравненные) уровни (читается как «игрек, выравненный по t»); t – условное обозначение времени (1, 2, 3 …); a0, a1, a2, ... – параметры аналитической функции; k – число гармоник (при выравнивании по ряду Фурье).
Выбор той или иной функции для выравнивания ряда динамики осуществляется на основании графического изображения эмпирических данных. Если по тем или иным причинам уровни эмпирического ряда трудно описать одной функцией, следует разбить анализируемый период на отдельные части и затем выровнять каждую часть по соответствующей кривой.
Таблица 15. Виды математических функций, используемые при выравнивании
| Название функции | Вид функции | Формула |
| Прямая линия | 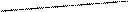
| 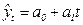 (65) (65)
|
| Парабола 2-го порядка |   или или
| 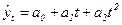 (66) (66)
|
| Парабола 3-го порядка | 
| 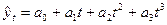 (67) (67)
|
| Гипербола | 
| 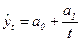 (68) (68)
|
| Показательная | 
| 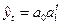 (69) (69)
|
| Степенная | 
| 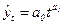 (70) (70)
|
| Ряд Фурье | 
| 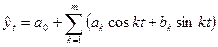 (71) (71)
|
Нередко один и тот же ряд можно выровнять по разным аналитическим функциям и получить довольно близкие результаты. В нашем примере про ВО России можно произвести выравнивание и по прямой линии, и по параболе. Чтобы решить вопрос о том, использование какой кривой дает лучший результат, обычно сопоставляют суммы квадратов отклонений эмпирических уровней от теоретических (остатки), рассчитанным по разным функциям, то есть:
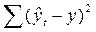 . (72)
. (72)
Та функция, при которой эта сумма минимальна, считается наиболее адекватной, приемлемой. Однако сравнивать непосредственно суммы квадратов отклонений можно в том случае, если сравниваемые уравнения имеют одинаковое число параметров. Если же число параметров k разное, то каждую сумму квадратов делят на разность (n – k), выступающую в роли числа степеней свободы, и сравнивают уже квадраты отклонений уровней, рассчитанные на одну степень свободы (т.е. остаточные дисперсии на одну степень свободы).
Параметры искомых уравнений (a0, a1, a2, ...) при аналитическом выравнивании могут быть определены по-разному, но наиболее распространенным методом является метод наименьших квадратов (МНК). При этом методе учитываются все эмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней y от теоретических уровней 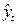 :
:
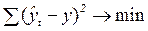 . (73)
. (73)
В частности, при выравнивании по прямой вида (65) параметры 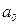 и
и 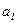 отыскиваются по МНК следующим образом. В формуле (73) вместо
отыскиваются по МНК следующим образом. В формуле (73) вместо 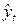 записываем его конкретное выражение
записываем его конкретное выражение 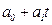 . Тогда
. Тогда 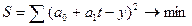 . Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении
. Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении 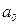 и
и 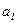 функция двух переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по
функция двух переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по 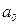 и
и 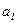 , приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
, приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
В соответствии с вышеизложенным найдем частные производные:
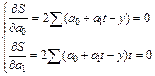
Сократив каждое уравнение на 2, раскрыв скобки и перенеся члены с y в правую сторону, а остальные – оставив в левой, получим систему нормальных уравнений:
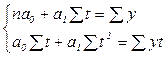 (74)
(74)
где n – количество уровней ряда; t – порядковый номер в условном обозначении периода или момента времени; y – уровни эмпирического ряда.
Эта система и, соответственно, расчет параметров 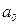 и
и 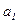 упрощаются, если отсчет времени ведется от середины ряда[13]. Например, при нечетном числе уровней (как в нашем примере про ВО России – 7 уровней) серединная точка времени (год, месяц) принимается за нуль, тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. (см. 3-й столбец табл. 16). При четном числе уровней два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала:
упрощаются, если отсчет времени ведется от середины ряда[13]. Например, при нечетном числе уровней (как в нашем примере про ВО России – 7 уровней) серединная точка времени (год, месяц) принимается за нуль, тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. (см. 3-й столбец табл. 16). При четном числе уровней два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала: 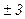 ,
, 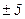 ,
, 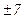 и т.д.
и т.д.
При таком порядке отсчета времени (от середины ряда) 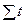 = 0, поэтому, система нормальных уравнений (74) упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:
= 0, поэтому, система нормальных уравнений (74) упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:
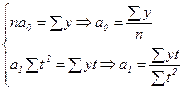 (75)
(75)
Как видим, при такой нумерации периодов параметр 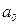 представляет собой средний уровень равномерного интервального ряда, то есть формулу (56). Определим по формуле (75) параметры уравнения прямой для нашего примера про ВО России, для чего исходные данные и все расчеты необходимых сумм представим в табл. 16.
представляет собой средний уровень равномерного интервального ряда, то есть формулу (56). Определим по формуле (75) параметры уравнения прямой для нашего примера про ВО России, для чего исходные данные и все расчеты необходимых сумм представим в табл. 16.
Таблица 16. Вспомогательные расчеты для линейного тренда
| Год | y | t | t2 | yt | 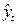
| 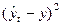
| 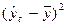
| 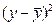
|
| 149,9 | -3 | -449,7 | 97,557 | 2739,775 | 25636,584 | 11614,681 | ||
| 155,6 | -2 | -311,2 | 150,929 | 21,822 | 11394,038 | 10418,577 | ||
| 168,3 | -1 | -168,3 | 204,300 | 1296,000 | 2848,509 | 7987,252 | ||
| 257,671 | 2085,879 | 0,000 | 2085,879 | |||||
| 280,6 | 280,6 | 311,043 | 926,768 | 2848,509 | 525,719 | |||
| 368,9 | 737,8 | 364,414 | 20,122 | 11394,038 | 12371,795 | |||
| 468,4 | 1405,2 | 417,786 | 2561,806 | 25636,584 | 44406,531 | |||
| Итого | 1803,7 | 1494,4 | 1803,700 | 9652,171 | 79758,263 | 89410,434 |
Из табл. 16 получаем, что: a0 = 1803,7/7 = 257,671 и a1 = 1494,4/28 = 53,371. Отсюда искомое уравнение тренда: 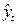 =257,671+53,371t. В 6-м столбце табл. 16 приведены теоретические (трендовые) уровни, рассчитанные по этому уравнению, а в итоге 7-го столбца – остатки по формуле (72). Для иллюстрации построим график эмпирических и трендовых уровней – рис. 6.
=257,671+53,371t. В 6-м столбце табл. 16 приведены теоретические (трендовые) уровни, рассчитанные по этому уравнению, а в итоге 7-го столбца – остатки по формуле (72). Для иллюстрации построим график эмпирических и трендовых уровней – рис. 6.
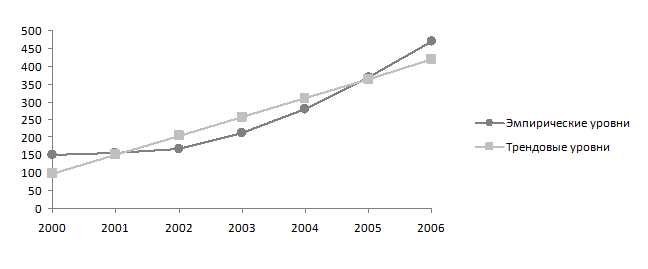
Рис. 6. Эмпирические и трендовые уровни ряда динамики ВО России
Дата добавления: 2017-03-29; просмотров: 612;
