Понятие корреляционной зависимости
Один из наиболее общих законов объективного мира – закон всеобщей связи и зависимости между явлениями. Естественно, что, исследуя явления в самых различных областях, статистика неизбежно сталкивается с зависимостями как между количественными, так и между качественными показателями, признаками. Ее задача – обнаружить (выявить) такие зависимости и дать им количественную характеристику.
Среди взаимосвязанных признаков (показателей) одни могут рассматриваться как определенные факторы, влияющие на изменение других (факторные), а вторые (результативные) – как следствие, результат влияния первых.
Существует 2 вида связи между отдельными признаками: функциональная и стохастическая (статистическая), частным случаем которой является корреляционная.
Связь между двумя переменными x и y называется функциональной, если определенному значению переменной x строго соответствует одно или несколько значений другой переменной y, и с изменением значения x значение y меняется строго определенно. Такие связи обычно встречаются в точных науках. Например, известно, что площадь квадрата равна квадрату его стороны (S = a2). Это соотношение характерно для каждого единичного случая (квадрата), это так называемая жестко детерминированная связь. Такие связи можно встретить и в области экономических явлений. Например, при простой сдельной оплате труда связь между оплатой труда y и количеством изготовленных изделий x при фиксированной расценке за одну деталь, например 5 руб., легко выразить формулой 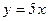 .. Для изучения функциональных связей применяется индексный метод, которыйрассматривается в теме 7.
.. Для изучения функциональных связей применяется индексный метод, которыйрассматривается в теме 7.
Существуют и иного рода связи, где взаимно действуют многие факторы, комбинация которых приводит к вариации значений результативного признака (показателя) при одинаковом значении факторного признака. Например, при изучении зависимости величины таможенных платежей, поступающих в федеральный бюджет, от количества товаров, перемещаемых через таможенную границу государства, (или от стоимостного товарооборота) последние будут рассматриваться как факторный признак, а величина таможенных платежей – как результативный. Между ними нет жестко детерминированной связи, т.е. при одном и том же количестве перемещенных через таможенную границу товаров (или стоимости товарооборота) величина таможенных платежей, перечисленных разными таможнями будет различной, так как кроме количества товаров, перемещаемых через таможенную границу государства, (или стоимость товарооборота) на величину таможенных платежей влияет много других факторов (различная номенклатура товаров, для которых применяются различные таможенные пошлины, сборы и льготы; различные таможенные режимы перемещения товаров через таможенную границу и др.), комбинация которых вызывает вариацию величины таможенных платежей.
Там, где взаимодействует множество факторов, в том числе и случайных, выявить зависимости, рассматривая единичный случай, невозможно. Такие связи можно обнаружить только при массовом наблюдении как статистические закономерности[15]. Выявленная таким образом связь именуется стохастической[16].
Корреляционная связь[17] – понятие более узкое, чем стохастическая связь, это ее частный случай. Именно корреляционные связи являются предметом изучения статистики.
Корреляционная связь – это связь, проявляющаяся при большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и признаками-факторами. Другими словами, корреляционную связь условно можно рассматривать как своего рода функциональную связь средней величины одного признака (результативного) со значением другого (или других). При этом, если рассматривается связь средней величины результативного показателя y с одним признаком-фактором x, корреляция называется парной, а если факторных признаков 2 и более (x1, x2, …, xm) – множественной[18].
По характеру изменений x и y в парной корреляции различают прямую и обратную связь. При прямой связи значения обоих признаков изменяются в одном направлении, т.е. с увеличением (уменьшением) значений x увеличиваются (уменьшаются) и значения y. При обратной связи значения факторного и результативного признаков изменяются в разных направлениях.
Изучение корреляционных связей сводится в основном к решению следующих задач:
1) выявление наличия (отсутствия) корреляционной связи между изучаемыми признаками;
2) измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов (эта часть исследования именуется корреляционным анализом);
3) определение уравнения регрессии – математической модели, в которой среднее значение результативного признака у рассматривается как функция одной или нескольких переменных – факторных признаков (эта часть исследования именуется регрессионным анализом).
Общий термин «корреляционно-регрессионный анализ» подразумевает всестороннее исследование корреляционных связей (т.е. решение всех трех задач).
Корреляционно-регрессионный анализ находит широкое применение в статистике. Рассмотрим его практическое применение на примере данных таможенной статистики внешней торговли России в 2006 году – таблица 18.
Таблица 18. Величина внешнеторгового оборота и таможенных платежей
| Месяц | Оборот, млрд.долл. | Платеж, млрд.руб. |
| Январь | 27,068 | 172,17 |
| Февраль | 29,889 | 200,90 |
| Март | 34,444 | 231,83 |
| Апрель | 33,158 | 232,10 |
| Май | 37,755 | 233,40 |
| Июнь | 37,554 | 236,99 |
| Июль | 37,299 | 246,53 |
| Август | 40,370 | 253,62 |
| Сентябрь | 37,909 | 256,43 |
| Октябрь | 38,348 | 261,89 |
| Ноябрь | 39,137 | 259,36 |
| Декабрь | 46,298 | 278,87 |
В качестве факторного признака x примем стоимостной внешнеторговый товарооборот в млрд. долл. США, а в качестве результативного признака y – величину таможенных платежей в федеральный бюджет в млрд. руб.
| x | y |
| 27,068 | 172,17 |
| 29,889 | 200,90 |
| 33,158 | 232,10 |
| 34,444 | 231,83 |
| 37,299 | 246,53 |
| 37,554 | 236,99 |
| 37,755 | 233,40 |
| 37,909 | 256,43 |
| 38,348 | 261,89 |
| 39,137 | 259,36 |
| 40,370 | 253,62 |
| 46,298 | 278,87 |
Дата добавления: 2017-03-29; просмотров: 567;
