Процесс принятия решения о выборе кандидата на должность главного менеджера
За несколько недель для дальнейшего рассмотрения были выбраны семь кандидатов. Им было предложено заполнить стандартную анкету, а после этого прийти на собеседование. Некоторые ответы на вопросы стандартной анкеты для исследования не понадобятся. Они заданы для знакомства с кандидатом, для сбора сведений о нем в случае, если он будет принят на работу и т.д. Самые важные данные и факты отмечены в критериях отбора. Некоторые пункты представлены сразу в числовом виде. Например, ответы на вопросы в собеседовании оцениваются экспертом по шкале от 1 до 10.
Данные о претендентах представлены в электронной таблице в соответствии с рисунком 11.
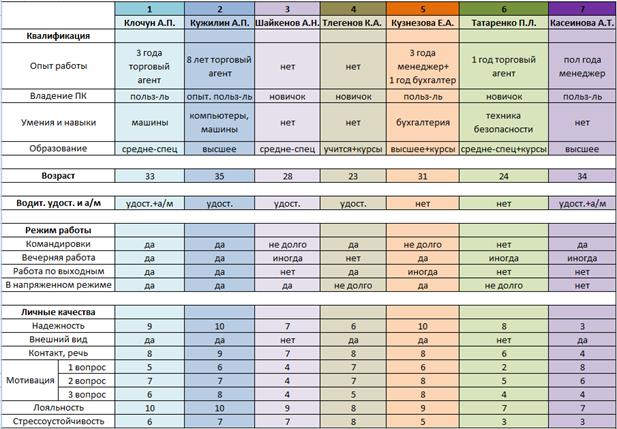
Рисунок 11. Информация о претендентах
Необходимо ввести систему оценок, чтобы представить данные для расчетов в числовом виде:
1) опыт работы:
· стаж: оценка от 0 до 3. 0 – нет опыта работы, 1 – небольшой опыт (до 1 года), 2 – средний опыт (от 1 года до 3 лет), 3 – большой опыт (от 3 лет);
· сфера: 0 – нет, 1 – торговля, 1 – управление, 2 – торговля и управление;
2) владение ПК: 0 – не владеет, 1 – новичок, 2 – пользователь, 3 – опытный пользователь;
3) умения и навыки: 0 – нет, 1 – за каждый навык;
4) образование: 1 – учится, 2 – средне-специальное, 3 – высшее, курсы – 1 дополнительный балл.
Составляющие критериев не равнозначны. Весовые коэффициенты для критерия «квалификация»: опыт работы – 0,36; владение ПК – 0,21; умения и навыки – 0,14; образование – 0,29.
Аналогично для критерия «Режим работы»: 0 – не согласен, 1 – согласен иногда (недолго, временно), 2 – полностью согласен.
Для критерия «Водительское удостоверение и автомобиль»: 0 – не имеет ничего, 1 – имеется удостоверение, 2 – имеются удостоверение и автомобиль.
Таким образом, можно подсчитать количество набранных претендентом баллов по каждому критерию.
Оценки кандидатов представлены в электронной таблице в соответствии с рисунком 12.

Рисунок 12. Оценки претендентов
В соответствии с этапами логического вывода, первый шаг – фаззификация, то есть определение значений функций принадлежностей для каждого из кандидатов по пяти критериям.
Для этого необходимо задать функции принадлежности, соответствующие каждому критерию.
Каждый критерий является лингвистической переменной.
Название первой лингвистической переменной – «Квалификация». Сформируем для нее базовое терм-множество, которое состоит только из одной нечеткой переменной «Подходящая», а область рассуждений – в виде 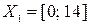 . Функция принадлежности гауссова типа задана следующей формулой:
. Функция принадлежности гауссова типа задана следующей формулой:
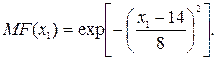
Графическое изображение функции принадлежности для критерия «Квалификация» представлено на рисунке 13.
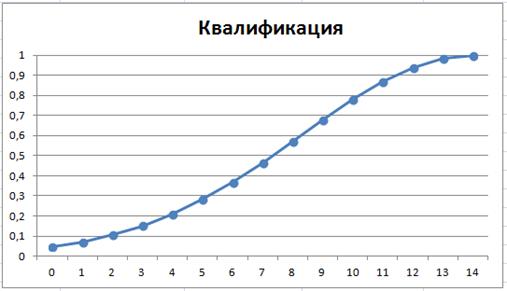
Рисунок 13. Функция принадлежности для критерия «Квалификация»
Название второй лингвистической переменной – «Возраст». Сформируем для нее базовое терм-множество, которое состоит только из одной нечеткой переменной «Оптимальный», а область рассуждений в виде 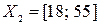 . Функция принадлежности гауссова типа задана следующей формулой:
. Функция принадлежности гауссова типа задана следующей формулой:
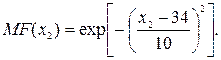
Графическое изображение функции принадлежности для критерия «Возраст» представлено на рисунке 14.
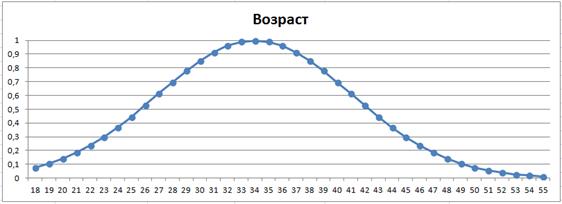
Рисунок 14. Функция принадлежности для критерия «Возраст»
Название третьей лингвистической переменной – «Водительское удостоверение и а/м». Сформируем для нее базовое терм-множество, которое состоит только из одной нечеткой переменной «Имеется», а область рассуждений в виде 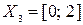 . Кусочно-линейная функция принадлежности задана следующей формулой:
. Кусочно-линейная функция принадлежности задана следующей формулой:
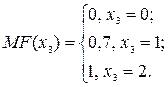
Название четвертой лингвистической переменной – «Режим работы». Сформируем для нее базовое терм-множество, которое состоит только из одной нечеткой переменной «Устраивает», а область рассуждений в виде 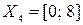 . Функция принадлежности гауссова типа задана следующей формулой:
. Функция принадлежности гауссова типа задана следующей формулой:
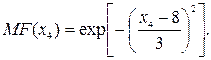
Графическое изображение функции принадлежности для критерия «Режим работы» представлено на рисунке 15.
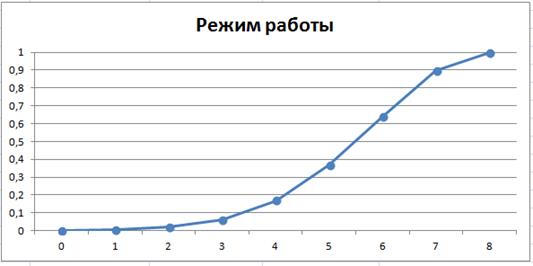
Рисунок 15. Функция принадлежности для критерия «Режим работы»
Название пятой лингвистической переменной – «Личные качества». Сформируем для нее базовое терм-множество, которое состоит только из одной нечеткой переменной «Обладает», а область рассуждений в виде 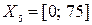 . Функция принадлежности гауссова типа задана следующей формулой:
. Функция принадлежности гауссова типа задана следующей формулой:
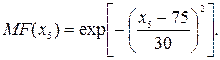
Графическое изображение функции принадлежности для критерия «Личные качества» представлено на рисунке 16.
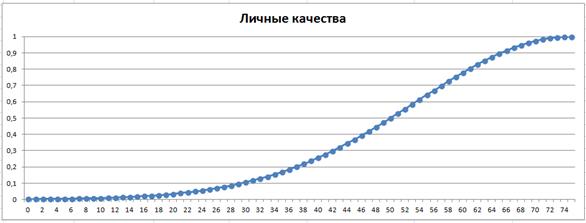
Рисунок 16. Функция принадлежности для критерия «Личные качества»
Таким образом, получаем следующую таблицу, представленную на рисунке 17.

Рисунок 17. Оценки кандидатов
Следующий этап нечеткого вывода – разработка нечетких правил. Обсуждение среди руководства фирмы о том, по каким правилам оценивать претендентов, дало следующий результат:
· 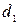 : «Если кандидат не имеет подходящей квалификации и не обладает нужными личными качествами, то он – неудовлетворяющий»;
: «Если кандидат не имеет подходящей квалификации и не обладает нужными личными качествами, то он – неудовлетворяющий»;
· 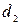 : «Если кандидата устраивают условия работы, и он обладает нужными личными качествами, то он – средне удовлетворяющий»;
: «Если кандидата устраивают условия работы, и он обладает нужными личными качествами, то он – средне удовлетворяющий»;
· 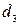 : «Если кандидат имеет подходящую квалификацию, обладает нужными личными качествами, но у него нет автомобиля и водительского удостоверения, то он – средне удовлетворяющий»;
: «Если кандидат имеет подходящую квалификацию, обладает нужными личными качествами, но у него нет автомобиля и водительского удостоверения, то он – средне удовлетворяющий»;
· 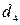 : «Если кандидат имеет подходящую квалификацию, его возраст – оптимален и он обладает нужными личными качествами, то он – удовлетворяющий»;
: «Если кандидат имеет подходящую квалификацию, его возраст – оптимален и он обладает нужными личными качествами, то он – удовлетворяющий»;
· 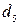 : «Если кандидат имеет подходящую квалификацию, его возраст – оптимальный, его устраивают условия работы, и он обладает нужными личными качествами, то он – очень удовлетворяющий»;
: «Если кандидат имеет подходящую квалификацию, его возраст – оптимальный, его устраивают условия работы, и он обладает нужными личными качествами, то он – очень удовлетворяющий»;
· 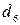 : «Если кандидат имеет подходящую квалификацию, его возраст – оптимальный, у него имеются водительское удостоверение и автомобиль, его устраивают условия работы и он обладает нужными личными качествами, то он – безупречный».
: «Если кандидат имеет подходящую квалификацию, его возраст – оптимальный, у него имеются водительское удостоверение и автомобиль, его устраивают условия работы и он обладает нужными личными качествами, то он – безупречный».
Анализ приведенных информационных фрагментов позволяет выявить шесть критериев, используемых для принятия решения: 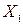 – квалификация,
– квалификация, 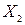 – возраст,
– возраст, 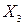 – наличие водительского удостоверения и автомобиля,
– наличие водительского удостоверения и автомобиля, 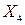 – условия работы,
– условия работы, 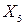 – личные качества,
– личные качества, 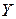 – удовлетворительность.
– удовлетворительность.
Для формулировки правил следует определить возможные значения 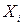 и
и 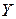 , которые будут использоваться для оценки кандидатов:
, которые будут использоваться для оценки кандидатов:
· 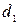 : «Если
: «Если 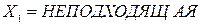 и
и 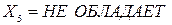 , то
, то 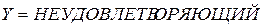 »;
»;
· 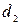 : «Если
: «Если 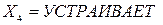 и
и 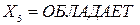 , то
, то 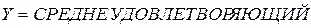 »;
»;
· 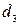 : «Если
: «Если 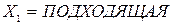 и
и 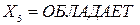 и
и 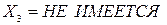 , то
, то 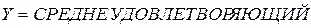 »;
»;
· 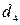 : «Если
: «Если 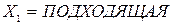 и
и 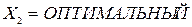 и
и 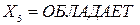 , то
, то 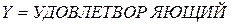 »;
»;
· 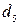 : «Если
: «Если 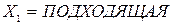 и
и 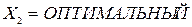 и
и 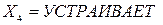 и
и 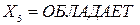 , то
, то 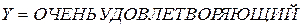 »;
»;
· 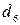 : «Если
: «Если 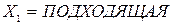 и
и 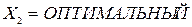 и
и 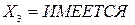 и
и 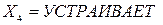 и
и 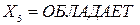 , то
, то 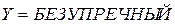 ».
».
Переменная 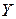 задана на множестве
задана на множестве
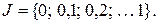
Значения переменной 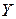 заданы с помощью следующих функций принадлежности:
заданы с помощью следующих функций принадлежности:
· 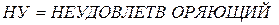 определено как
определено как
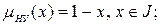
· 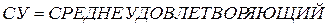 определено как
определено как
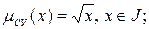
· 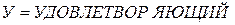 определено как
определено как
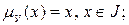
· 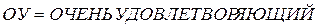 определено как
определено как
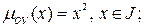
· 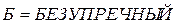 определено как
определено как
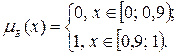
Графически значения переменной 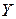 , заданные с помощью функций принадлежности, представлены на рисунке 18.
, заданные с помощью функций принадлежности, представлены на рисунке 18.
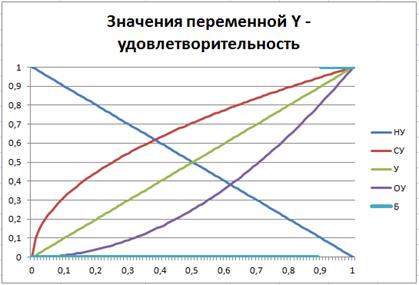
Рисунок 18. Значения переменной 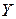 , заданные с помощью функций принадлежности
, заданные с помощью функций принадлежности
Выбор производится из семи кандидатов на множестве
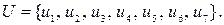
Оценки кандидатов заданы следующими нечеткими множествами, представленными на рисунке 19:
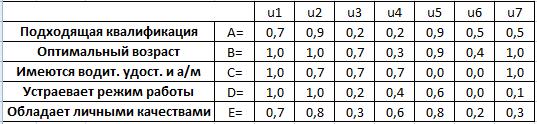
Рисунок 19. Оценки кандидатов с помощью нечетких множеств
С учетом введенных обозначений правила 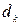 принимают вид:
принимают вид:
· 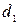 : «Если
: «Если 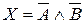 , то
, то 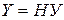 »;
»;
· 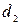 : «Если
: «Если 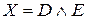 , то
, то 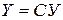 »;
»;
· 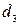 : «Если
: «Если 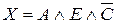 , то
, то 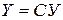 »;
»;
· 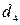 : «Если
: «Если 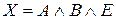 , то
, то 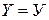 »;
»;
· 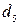 : «Если
: «Если 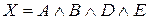 , то
, то 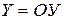 »;
»;
· 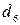 : «Если
: «Если 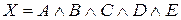 , то
, то 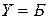 ».
».
Предположим, что все критерии равнозначны, то есть их весовые коэффициенты равны.
Вычислим функции принадлежности для 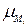 для левых частей приведенных правил по формуле:
для левых частей приведенных правил по формуле:
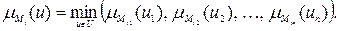
Получаем следующие значения (рисунок 20):
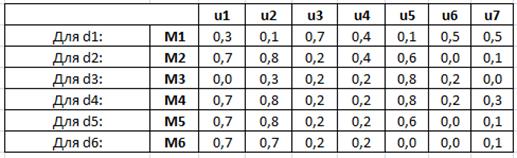
Рисунок 20. Значения функций принадлежности 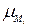
Теперь правила можно записать в виде:
· 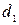 : «Если
: «Если 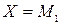 , то
, то 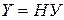 »;
»;
· 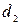 : «Если
: «Если 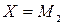 , то
, то 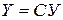 »;
»;
· 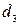 : «Если
: «Если 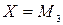 , то
, то 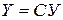 »;
»;
· 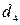 : «Если
: «Если 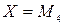 , то
, то 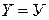 »;
»;
· 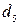 : «Если
: «Если 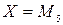 , то
, то 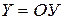 »;
»;
· 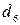 : «Если
: «Если 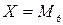 , то
, то 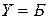 ».
».
Используя для преобразования правил вида «Если 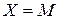 , то
, то 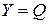 » импликацию Лукасевича:
» импликацию Лукасевича:
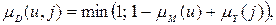
для каждой пары 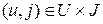 получаем следующие нечеткие отношения, представленные на рисунке 21:
получаем следующие нечеткие отношения, представленные на рисунке 21:
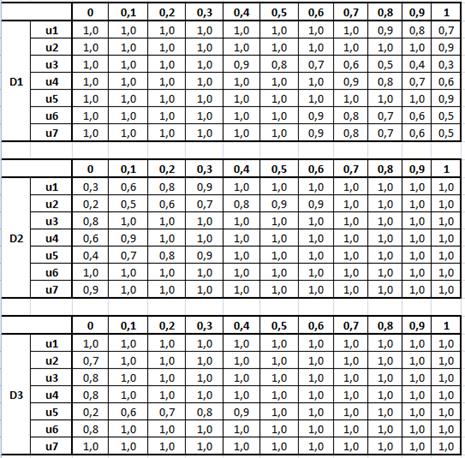
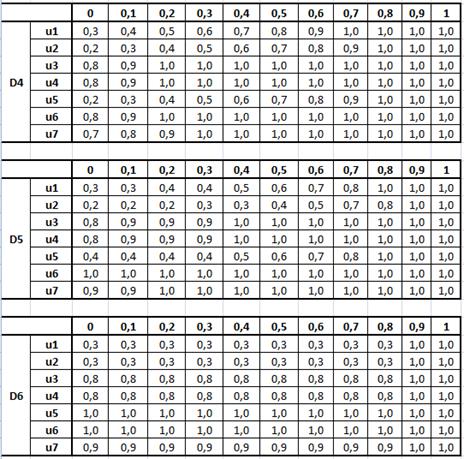
Рисунок 21. Нечеткие отношения 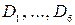
В результате пересечения отношений 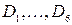 получаем общее функциональное решение, представленное на рисунке 22:
получаем общее функциональное решение, представленное на рисунке 22:
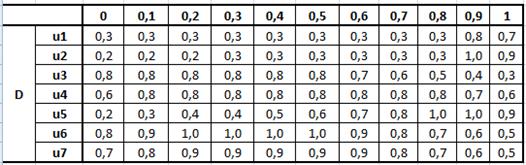
Рисунок 22. Общее функциональное решение
Для вычисления удовлетворительности каждой из альтернатив применяем правило композиционного вывода в нечеткой среде:
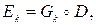
где 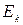 – степень удовлетворения альтернативы
– степень удовлетворения альтернативы 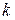 ,
,
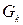 – отображение альтернативы
– отображение альтернативы 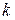 в виде нечеткого подмножества на
в виде нечеткого подмножества на 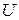 ,
,
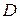 – общее функциональное решение.
– общее функциональное решение.
Тогда
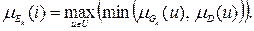
Сопоставление альтернатив происходит на основе точечных оценок. Для нечеткого подмножества 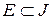 определяем
определяем 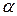 -уровневое множество (
-уровневое множество ( 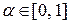 ):
):
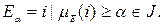
Уровневые подмножества 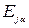 и мощность такого подмножества
и мощность такого подмножества 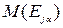 вычисляем по формуле:
вычисляем по формуле:
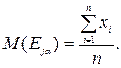
Точечную оценку 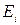 находим по формуле:
находим по формуле:
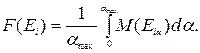
Для первой альтернативы вычисляем уровневые множества и мощность такого множества:
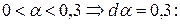
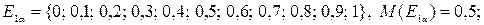
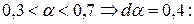
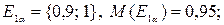
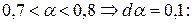
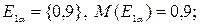
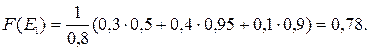
Аналогично находим точечные оценки для других альтернатив:
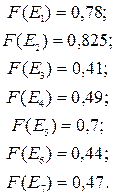
В качестве лучшей выбираем альтернативу, имеющую наибольшую точечную оценку. В данном случае это альтернатива 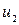 , следовательно, она и будет наилучшей.
, следовательно, она и будет наилучшей.
Однако довольно большие точечные оценки имеют также альтернативы под номерами 1 и 2. Если внимательно посмотреть на исходные оценки кандидатов на рисунке 17, то можно увидеть, что большая разница между кандидатом номер 5 и двумя другими, имеющими наивысшие оценки, заключается в критерии «Наличие водительского удостоверения и а/м». При условии, что критерии при выборе решено считать однозначными, появление у претендента номер 5 водительского удостоверения может изменить его конечную точечную оценку. Остальные данные никак не смогут измениться за короткий промежуток времени, поэтому допускаем только один альтернативный случай.
Предположив, что претендент номер 5 имеет водительское удостоверение, и, изменив начальные данные, получаем общее функциональное решение, представленное на рисунке 23:
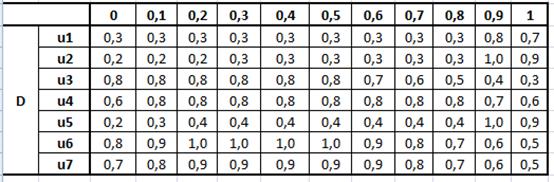
Рисунок 23. Общее функциональное решение при изменении начальных условий
Заново проведя расчеты конечных точечных оценок, получаем следующий результат:
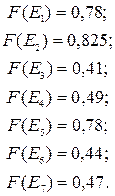
Теперь кандидаты под номерами 1 и 5 имеют одинаковые точечные оценки, а значит, они одинаково подходят на должность главного менеджера по продажам. Но все же лучшей остается альтернатива под номером 2.
Данный результат получен для случая, когда критерии имеют одинаковую важность.
Далее рассмотрим случай, когда предложенные критерии являются неравнозначными.
Коэффициенты относительной важности критериев определяются на основе процедуры парного сравнения критериев [30]. Сначала формируется матрица 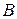 , элементы которой находятся с помощью таблицы 6 и удовлетворяют следующим условиям:
, элементы которой находятся с помощью таблицы 6 и удовлетворяют следующим условиям:
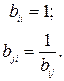
Таблица 6. Шкала оценок важности
Относительная важность критериев 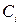 и и 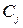
| Элемент 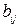
|
| Равная важность | |
| Немного важнее | |
| Важнее | |
| Заметно важнее | |
| Намного важнее | |
| Промежуточные значения | 2, 4, 6, 8 |
Таким образом, сформированная матрица 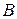 имеет вид:
имеет вид:
 .
.
Затем находится собственный вектор 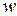 матрицы
матрицы 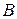 :
:
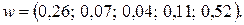
Каждому из критериев приписывается число 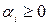 по следующему принципу: чем важнее критерий, тем больше
по следующему принципу: чем важнее критерий, тем больше 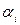 . Значения коэффициентов
. Значения коэффициентов 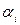 получаются умножением элементов
получаются умножением элементов 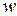 на
на 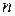 – число критериев:
– число критериев:
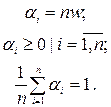
Таким образом, получаются следующие значения коэффициентов 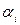 :
:
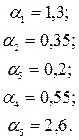
Учитывая найденные коэффициенты, нечеткие множества, характеризующие альтернативные варианты с точки зрения различных критериев вычисляются по формуле:
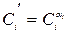
и принимают следующие значения, представленные на рисунке 24:
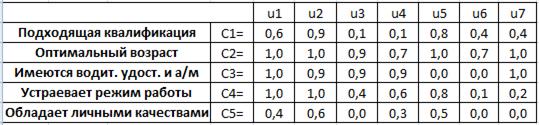
Рисунок 24. Оценки кандидатов с помощью нечетких множеств для неравнозначных критериев
Далее повторяются аналогичные действия, как и в случае нахождения наилучшей альтернативы при равнозначных критериях выбора. Общее функциональное решение в таком случае имеет вид, представленный на рисунке 25:
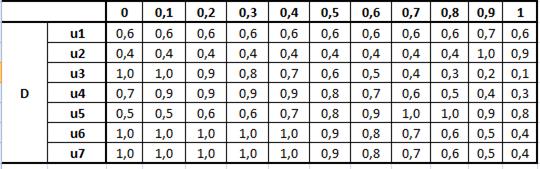
Рисунок 25. Общее функциональное решение в случае неравнозначных критериев выбора
Тогда точечные оценки каждого кандидата при неравнозначных критериях равны:
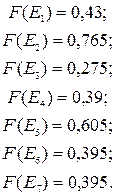
При неравнозначных критериях лучшим кандидатом остается кандидат под номером 2. Но ранее одинаково хорошие кандидаты под номерами 1 и 5 в данном случае таковыми не являются. Оценка претендента номер 5 значительно выше оценки претендента номер 1, что подтверждает выдвинутое ранее предположение, что отсутствие водительского удостоверения и автомобиля сильно повлияло на конечную оценку кандидата 5.
При окончательном выборе сотрудника на должность главного менеджера по продажам следует воспользоваться оценками, полученными при неравнозначных критериях, так как такая ситуация наиболее приближена к реальности. Главными критериями при выборе кандидата на такую высокую и ответственную должность являются личные качества, квалификация, умение работать с клиентами, принимать решения в сложных ситуациях и работать в коллективе.
Выполнение в вычислительной среде см.МУ МО СППР Ин(е)
Основные результаты УНИРС: Описан процесс принятия управленческих решений методом нечеткого логического вывода на примере предприятия ИП Пошивкин А.С.:
· выбор наилучшего кандидата на должность главного менеджера по продажам;
· оптимизация графика работы торговых агентов.
По результатам проведенного исследования в штат был принят менеджер, который показал хороший уровень знаний в вопросах управления и продажи, уже за небольшое время работы зарекомендовал себя как ответственный, целеустремленный, энергичный сотрудник, готовый учиться в процессе работы и применять свои знания, умения и навыки для улучшения работы предприятия, для его процветания.
Используя за основу разработанные нечеткие логические системы, можно оптимизировать работу предприятия, обеспечить принятие различных решений информационной поддержкой, что значительно сократит время и затраты для решения таких вопросов, как управление персоналом, составление графика работы, выбор партнеров, выбор оборудования и автотранспорта и многое другое.
Литература:
1.УМКД МОНОД Куликова (неопределенные данные)
2. Медиатека УИЛ ММСЭП, К.Владимирова Принятие решений на основе теории нечетких множеств (дипломная работа, 2014 г.)
[1] Желательно постоянно акцентировать различие между математическим моделированием и анализом данных. Математическое моделирование, как приближенное описание какого-либо класса явлений, начинается с формулировки законов, связывающих основные объекты модели, на основе изучения явлений и проникновения в них. Анализ данных не занимается разработкой методологии формирования системы показателей отображаемого объекта, а организует сбор, стандартную запись, систематизацию и обработку данных, в конечном итоге выделяя и упорядочивая результаты эксперимента, удобно представляя и интерпретируя их.
Дата добавления: 2019-10-16; просмотров: 675;
