Тема 1(6). Основные элементы

Нечеткий логический вывод. Нечеткие или приближенные рассуждения. Прямой (восходящий) логический вывод. Обратный (нисходящий) вывод. Нечеткое сравнение.

Режим повтора (Методы обработки неопределенных данных)

Многочисленные исследования показывают, что лица, принимающие решения без дополнительной аналитической поддержки, используют упрощенные, а иногда и противоречивые решающие правила. Поддержка принятия решения требуется во всех без исключения областях прикладной деятельности человека, что связано с увеличивающимся объемом информации, необходимостью учитывать большое количество противоречивых факторов, объективных и субъективных составляющих при принятии решений.

Элементы теории нечетких множеств успешно применяются для принятия решений. Экспертные оценки альтернативных вариантов по критериям могут быть представлены как нечеткие множества или числа, выраженные с помощью функций принадлежности. Для упорядочения нечетких чисел существует множество методов, которые отличаются друг от друга способом свертки и построения нечетких отношений. Последние можно определить как отношения предпочтительности между объектами.

В настоящее время для решения задачи многокритериального выбора становится распространенным использование методов с нечетким отношением предпочтения. Такие задачи являются более общими по сравнению с задачами с обычным отношением, а также они более приближены к реальности с точки зрения практики, так как однозначная предпочтительность одного варианта по сравнению с другими в обычной жизни является слишком жестким требованием.

Чаще всего у человека, принимающего решение, имеются аргументы за какой-либо вариант по сравнению с другим, но также есть и некоторые возражения. В таких случаях обычно говорят, что у него есть некоторая степень уверенности (оцениваемая числом от 0 до 1 или в процентах) в том, что один вариант из двух более предпочтителен.

Именно с такого рода данными и работает теория нечетких множеств. Применение функций принадлежности и всего механизма теории нечетких множеств – это, скорее, идея, так как на их основе разработано несколько методов, которые по-своему использует различные механизмы. Но одновременно с этим, они имеют и общие преимущества в сравнении с другими методами.

Методы многокритериального выбора альтернатив с использованием нечетких множеств [21]:

1) нечеткий вывод;

2) отношения предпочтения;

3) максиминная свертка;

4) аддитивная свертка.

Метод аддитивной свертки предполагает оптимистический подход. В этом случае низкие оценки по каждому критерию имеют одинаковый статус в сравнении с высокими. Метод максиминной свертки является реализацией пессимистического подхода. Он игнорирует хорошие аспекты альтернатив, тогда наилучшей считается альтернатива, которая имеет минимальные недостатки по всем критериям. Метод нечеткого вывода на правилах реализует эвристический подход [22]. В экспертных системах данный метод нашел широкое применение.

С учетом использования различных механизмов вероятно получение различных результатов. Хотя значения функции принадлежности отличны друг от друга, чаще всего общий порядок ранжирования совпадает. Несовпадение результатов, полученных различными методами, объясняется разными способами представления экспертной информации, а также различием подходов процессу принятия решений.

В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятиями, качеством продукции и технологическими процессами, при описании предпочтений потребителей и оптимизации процессов варки стали [23].

Основанные на теории нечетких множеств методы имеют общие свойства.

1) Методы, основанные на разных подходах, дают различные результаты. Каждый из подходов имеет свои особенности и ограничения, поэтому пользователь должен получить о них некоторое представление перед применением того или иного метода. Таким образом, главными трудностями многокритериального выбора с использованием нечетких моделей являются способы вычисления интегральных оценок и представление информации о взаимоотношениях между критериями. Эвристический подход дает наиболее широкие возможности для представления информации.

2) Основанные на нечетких моделях методы принятия решений позволяют качественно и удобно проводить оценку альтернатив по отдельным критериям. Добавление новых альтернатив, в отличие от других методов, не изменяет порядок наборов, ранжированных ранее. Оценка альтернатив по предложенным критериям возможна на основе точечных оценок при использовании функций принадлежности критериев. Также возможна и лингвистическая оценка.

3) Большинство методов принятия решений с использованием нечетких моделей показывает слабую устойчивость конечных результатов относительно начальных данных [24]. Считается, что метод, основанный на нечетких правилах, обладает наибольшей устойчивостью.

Преимуществами fuzzy-систем являются:

1) нечеткая формализация критериев оценки и сравнения: использование критериев «значительно», «большинство», «преимущественно», «достаточно» и т.д.;

2) возможность оперирования нечеткими входными данными, такими как результаты различных опросов, то есть значениями, которые нельзя задать однозначно, а также непрерывно изменяющиеся во времени значения;

3) возможность проведения качественных оценок как входных данных, так и выходных результатов: оперирование не только значениями используемых данных, но и их степенью достоверности;

4) возможность реализации быстрого моделирования очень сложных динамических систем и их сравнительного анализа с некоторой заданной степенью точности.

Нечеткие выводы

Человеческие знания могут быть представлены в виде нечеткого правила следующим образом:

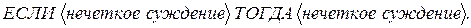
Нечеткие суждения делятся на два вида. Первый из них называется единичный (атомарный):

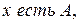
где 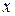– лингвистическая переменная,

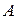–ее лингвистическое значение.

Второй тип называется композиционный и имеет вид:

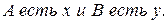
Второй тип представляет композицию атомарных суждений первого типа, соединенных операторами И, ИЛИ, НЕ. Эти операторы представлены как нечеткие пересечение, объединение и дополнение соответственно. Функция принадлежности для таких композиционных суждений вычисляется при помощи нечеткой импликации [16].

Нечеткие правила дают возможность выражать имеющиеся знания об отношениях между посылками и следствием. Для полного отображения этой информации часто необходимо использовать несколько сгруппированных правил.

Нечеткие правила объединяются в одно или несколько множеств на входе и связаны с нечетким множеством на выходе. Нечеткие множества в посылке связываются при помощи операторов И, ИЛИ, НЕ или лингвистическими модификациями.

Для нечетких множеств характерна схема нечеткого вывода, представленная на рисунке 9.

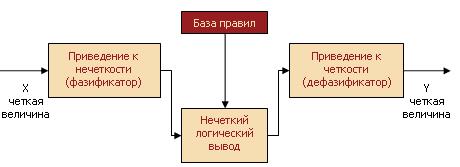
Рисунок 9. Нечеткая логическая схема

Такая совокупность также называется нечеткой логической системой, нечетким логическим контроллером, системой, основанной на правилах.

В основе представленной системы лежат правила по схеме «ЕСЛИ-ТОГДА», а также должны соблюдаться два условия:

1) существует хотя бы одно правило для каждого лингвистического терма выходной переменной;

2) для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).

Если эти правила не соблюдаются, то база нечетких правил является неполной. Если же имеется полная база правил, процесс логического вывода выполняется в четыре этапа.

Этап 1. Фаззификация.

На входе каждой нечеткой логической системы, основанной на правилах, находится информация по предложенным критериям об оценках альтернатив экспертами. Нечетко-множественный подход представления информации наиболее приближен к человеческому мышлению, но все же не является аналогичным. Поэтому необходимо провести процедуру фаззификации, которая состоит в определении степени истинности суждения, то есть в определении значения функции принадлежности для левых частей каждого правила.

Этап 2. Разработка нечетких правил.

На втором этапе определяются продукционные правила, связывающие лингвистические переменные. Множество таких правил описывает стратегию управления. Правила строятся по схеме «ЕСЛИ-ТОГДА».

Например, одно из правил для принятия решения о выборе наилучшего кандидата на некоторую должность: «Если кандидат не имеет подходящей квалификации и не обладает нужными личными качествами, то он – неудовлетворяющий».

Этап 3. Нечеткий вывод.

На первом шаге логического вывода необходимо определить степень принадлежности всей посылки правила. Для этого в нечеткой логике существуют два оператора: MIN(…) и MAX(…). MIN(…) вычисляет минимальное значение степени принадлежности, а MIN(…) – максимальное значение. В зависимости от того, какая связка используется в правиле, применяется один из этих двух операторов.

В процессе нечеткого вывода используется нечеткая импликация, которая может быть реализована различными способами.

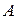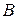Определение 1.15. Пусть и – это нечеткие множества, 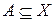, 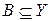. Нечеткой импликацией 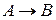называется отношение 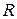, определенное на 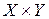и удовлетворяющее следующим правилам:

· правило типа minimum (правило Мамдани):

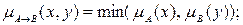
· правило типа «произведение» (правило Ларсена):

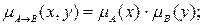
· правило Лукасевича:

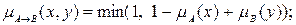
· правило типа min-max (правило Заде):

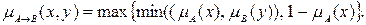
Набор этих правил не исчерпывает все известные из литературы определения нечеткой импликации. На данный момент их насчитывается более 40 штук. Преимущество одного из видов над другими на данный момент не доказано, поэтому на практике возможно применение любого из известных правил.

Этап 4. Дефаззификация.

Дефаззификацией называется процедура преобразования нечеткого множества в четкое число. Самым простым способом дефаззификации является выбор четкого числа с максимальной степенью принадлежности [16].

Наиболее распространенными способами выполнения операции дефаззификации являются преобразования функции принадлежности методами [25]:

· центра тяжести;

· медианы;

· центра максимумов.

Дефаззификация нечеткого множества 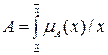по методу центра тяжести осуществляется по формуле:

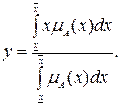
Физическим аналогом этой формулы является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества [26].

Дефаззификация нечеткого множества 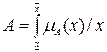методу медианы состоит в нахождении такого числа 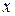, что:

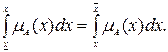
Геометрической интерпретацией метода медианы является нахождение такой точки на оси абсцисс, что перпендикуляр, восстановленный в этой точке, делит площадь под кривой функции принадлежности на две равные части [26].

Дефаззификация нечеткого множества по методу центра максимумов осуществляется по формуле:

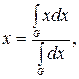
где 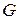– множество всех элементов из интервала 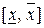, имеющих максимальную степень принадлежности нечеткому множеству .

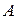В методе центра максимумов находится среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежностей. Если множество таких элементов конечно, то формула упрощается к следующему виду:

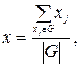
где 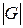– мощность множества .

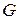Из этой формулы видно, что если функция принадлежности имеет только один максимум, то его координата и является четким аналогом нечеткого множества.

Этап дефаззификации считается законченным, когда для каждой из выходных лингвистических переменных будут определены итоговые количественные значения в форме некоторого действительного числа, то есть в ви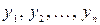де , где 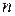– общее количество выходных лингвистических переменных в базе правил системы нечеткого вывода.

тема 2(6). Прикладные задачи принятия решений на основе теории нечетких множеств