Передаточная функция
1.1 Основные понятия
В качестве динамических характеристик при анализе и синтезе САУ широко используется передаточная функция, которая при решении ряда задач удобнее, чем дифференциальное уравнение. Передаточные функции применяются, когда надо по динамическим характеристикам звеньев определить динамические характеристики всей системы, исследовать устойчивость.
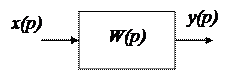 |
Передаточная функция 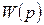 – отношение выходного сигнала
– отношение выходного сигнала 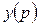 к входному
к входному 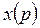 , преобразованных по Лапласу
, преобразованных по Лапласу
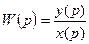 ,
,
здесь 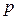 – параметр преобразования Лапласа.
– параметр преобразования Лапласа.
Передаточная функция полностью характеризует динамические свойства системы. Зная 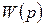 , можно определить переходный процесс на выходе системы.
, можно определить переходный процесс на выходе системы.
Переход из одного класса функций в другой позволяет вместо дифференциальных уравнений оперировать алгебраическими.
1.2. Преобразование Лапласа
Для определения передаточной функции используется преобразование Лапласа, которое определяется соотношением
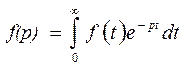 ,
,
здесь 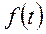 - функция времени (оригинал),
- функция времени (оригинал), 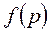 - функция параметра
- функция параметра 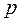 (изображение по Лапласу).
(изображение по Лапласу).
Иногда используют обозначения
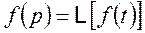 ,
,
здесь 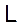 - оператор преобразования Лапласа.
- оператор преобразования Лапласа.
Обратное преобразование Лапласа:
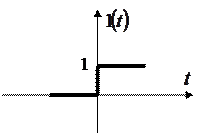
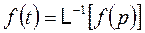 .
.
Пример: 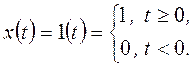
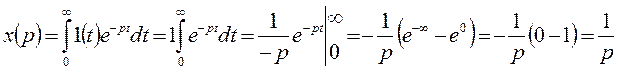
Для взятия преобразования Лапласа будем использовать таблицу преобразований Лапласа.
Таблица преобразований Лапласа
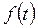 – функция времени (оригинал) – функция времени (оригинал)
| 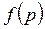 - изображение по Лапласу - изображение по Лапласу
|
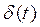
| |
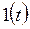
| 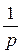
|
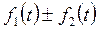
| 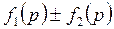
|
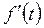
| 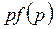 при нулевых нач. усл. при нулевых нач. усл.
|
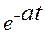
| 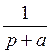
|
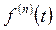
| 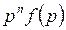 при нулевых нач. усл. при нулевых нач. усл.
|
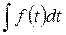
| 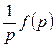
|
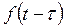
| 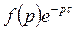
|
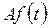
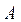 - константа - константа
| 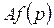
|
Например: функция времени равна 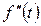 , тогда изображение по Лапласу будет равно
, тогда изображение по Лапласу будет равно 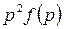 при нулевых начальных условиях.
при нулевых начальных условиях.
1.3 Переход от дифференциального уравнения
к передаточной функции и обратно
 |
Пример 1. Дано дифференциальное уравнение:
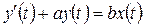
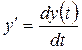
Получить передаточную функцию.
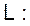
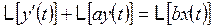
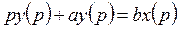
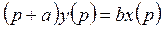
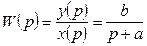 .
.
Пример 2. Дано дифференциальное уравнение:
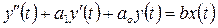
Получить передаточную функцию.
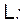
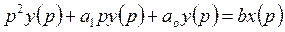
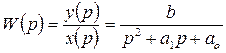 .
.
Правило: если задано дифференциальное уравнение, то чтобы получить передаточную функцию нужно: 1) производную 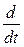 заменить на параметр преобразования Лапласа
заменить на параметр преобразования Лапласа 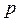 , т.е. взять преобразование Лапласа от дифференциального уравнения; 2) записать отношение преобразования Лапласа выхода
, т.е. взять преобразование Лапласа от дифференциального уравнения; 2) записать отношение преобразования Лапласа выхода 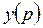 ко входу
ко входу 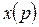 , т.е. получить
, т.е. получить 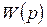 .
.
Пример 3. Задана передаточная функция:
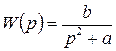
Получить дифференциальное уравнение.
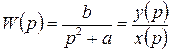
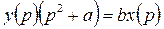
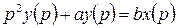
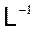 :
: 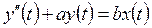 .
.
Правило: если задана передаточная функция, то чтобы получить дифференциальное уравнение нужно: 1) записать отношение преобразования Лапласа выхода 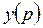 ко входу
ко входу 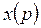 ; 2) перейти от равенства дробей к уравнению; 3) взять обратное преобразование Лапласа, т.е. параметр преобразования Лапласа
; 2) перейти от равенства дробей к уравнению; 3) взять обратное преобразование Лапласа, т.е. параметр преобразования Лапласа 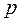 заменить на производную
заменить на производную 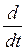 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Вторая форма записи. |
Дата добавления: 2019-10-16; просмотров: 511;
