Вторая форма записи.

Частотные характеристики

Амплитудно-фазовой частотной характеристикой системы (частотной передаточной функцией) 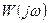называется отношение преобразованных по Фурье выходного сигнала 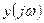к входному сигналу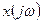

,

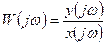где 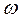- круговая частота. представляет собой комплексное число, т.е. вектор и может записываться в двух формах.

Первая форма записи через амплитуду и фазу

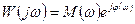, здесь 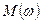- амплитудно-частотная характеристика, - фазо-частотная характеристика.

Амплитудно-частотная характеристика – зависимость отношения амплитуды выходного сигнала к входному от частоты.

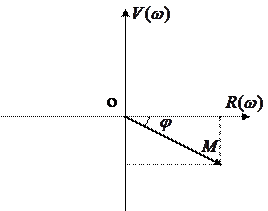Фазо-частотная характеристика характеризует сдвиг фазы выходного сигнала по отношению к входному сигналу.

M – модуль (длина вектора),

- угол сдвига фаз.

Вторая форма записи.

Используют представление вектора 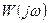в виде действительной и мнимой части, т.е.

,

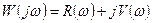где 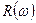- действительная часть, 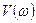- мнимая часть, 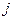- мнимая единица ( ).

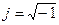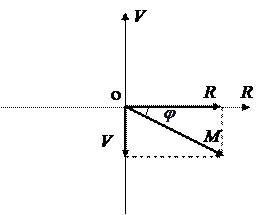Для перехода от одной формы записи к другой используются следующие формулы:

,

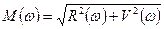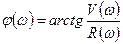, т.к. 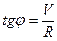- отношение противолежащего катета к прилежащему, то ,

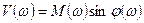(sin – отношение противолежащего катета к гипотенузе),

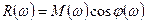(cos – отношение прилежащего катета к гипотенузе).

Связь частотных характеристик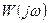

с дифференциальными уравнениями (ДУ)

Для перехода от дифференциальных уравнений (ДУ) к частотным характеристикам 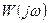надо производную 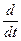заменить на .

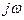Пример.

Дано дифференциальное уравнение

Получить амплитудно-фазовую частотную характеристику.

;

.

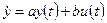
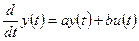
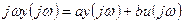
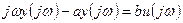
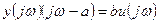
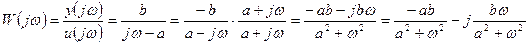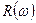
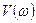
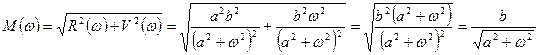Связь передаточной функции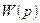

с частотными характеристиками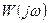

Для перехода от передаточной функции 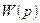к частотным характеристикам 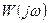надо параметр преобразования по Лапласу 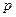заменить на .

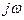Пример.

Задана передаточная функция .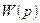

Получить амплитудно-фазовую частотную характеристику.

.

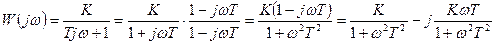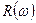
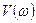
Область применения частотных характеристик

1. Обладают положительными свойствами передаточных функций, т.е. по частотным характеристикам отдельных звеньев можно находить частотные характеристики системы.

2. Их можно определять экспериментально, подавая на вход синусоиды разной частоты и измеряя амплитуду и фазу на выходе.

3. Их удобно представлять графически и определять по графикам свойства систем (устойчивость и т.д.)