Возможные виды корней и решения ДУ
Устойчивость. Основные понятия
Устойчивость - это способность системы, выведенной из состояния равновесия под влиянием возмущающих и управляющих воздействий, с течением времени прийти в равновесное состояние.
Автоматическую систему управления называют устойчивой, если она за счет своих внутренних сил возвращается в состояние установившегося равновесия после устранения непланируемого воздействия (возмущения).
Систему считают неустойчивой, если при сколь угодно малых отклонениях от состояния установившегося равновесия она не возвращается к этому состоянию, а непрерывно удаляется от него или совершает около него недопустимо большие колебания.
Например, если шарик совершает движение по желобу, то при малых отклонениях шарика, не выходящих за края желоба, его движение будет устойчивым, а при больших отклонениях – неустойчивым.
Устойчивость – это свойство, которым должна обладать любая САР.
2. Условия устойчивости линейной системы
Критерии устойчивости подразделяются на алгебраические и частотные.
Анализ устойчивости выполняется с помощью условий и критериев.
В общем случае процесс динамики линейной САР описывается ДУ (при заданных начальных условиях и воздействиях)
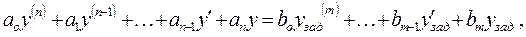 (1)
(1)
где 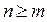
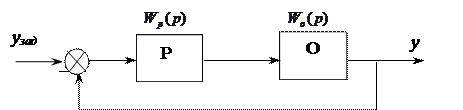 |
Для замкнутой САР при заданных динамических характеристиках объекта и регулятора характеристическое уравнение удобно находить с использованием передаточных функций. Для этого надо записать передаточные функции разомкнутой и замкнутой САР. Например: регулятор – П (пропорциональный), объект – А (апериодическое звено).
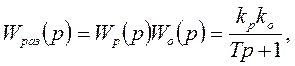
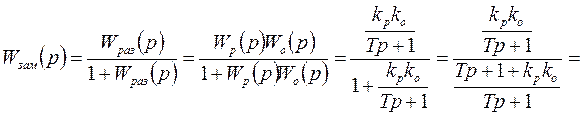
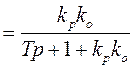 .
.
Характеристическое уравнение получается приравниванием к нулю знаменателя передаточной функции 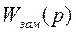 , т.е.
, т.е.
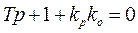 .
.
Характер изменения 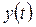 определяется корнями характеристического уравнения. Левую часть уравнения (1) приравниваем к нулю и заменим
определяется корнями характеристического уравнения. Левую часть уравнения (1) приравниваем к нулю и заменим 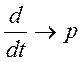
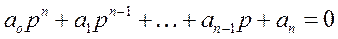 (2)
(2)
Например: 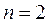
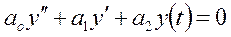
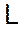 :
: 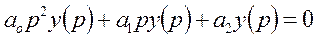
Делим на левую и правую часть на 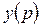
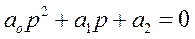
Возможные виды корней и решения ДУ
1) вещественные и разные, т.е.
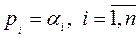 n - порядок д.у.
n - порядок д.у.
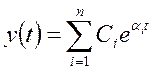 . (3)
. (3)
Пример. 1
Дано характеристическое уравнение 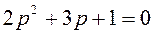 ,
,
n=2,
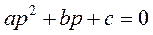 ,
,
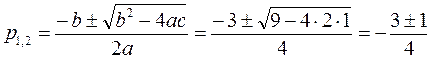 ,
,
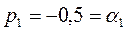 ;
; 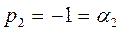 ,
,
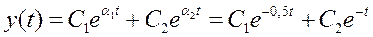 ,
,
Пусть С1=1; С2=2, тогда 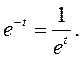
| t | |||||||||
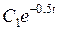
| 0,6 | 0,37 | 0,22 | 0,14 | 0,08 | 0,05 | 0,03 | 0,02 | |
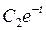
| 0,73 | 0,27 | 0,1 | 0,04 | 0,013 | 0,004 | 0,002 | 0,001 | |
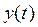
| 1,33 | 0,64 | 0,32 | 0,18 | 0,11 | 0,05 | 0,032 | 0,011 |
 |
Пример. 2
Дано характеристическое уравнение 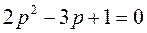 ,
,
n=2,
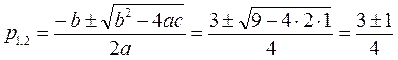 ,
,
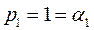 ;
; 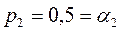 ,
,
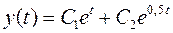 ,
,
Пусть С1=2, С2 =1,тогда
| t | 0,5 | 1,5 | 2,5 | ||||
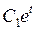
| 3,3 | 5,44 | 8,96 | 14,78 | 24,36 | 40,2 | |
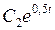
| 1,28 | 1,65 | 2,12 | 2,72 | 3,5 | 4,48 | |
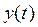
| 4,58 | 7,09 | 11,08 | 17,5 | 27,86 | 44,68 |
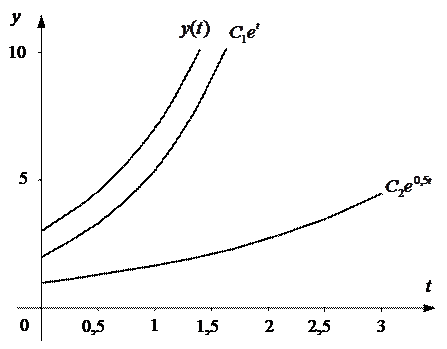 |
2) вещественные и одинаковые,т.е.
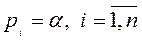 n - порядок д.у.
n - порядок д.у.
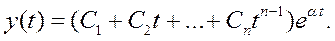
Пример. 1
Дано характеристическое уравнение 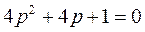 ,
,
n=2,
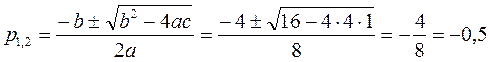 ,
,
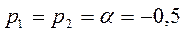 ,
,
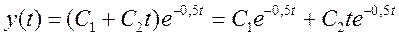 ,
,
Пусть С1=1; С2=2, тогда
| t | ||||||||
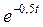
| 0,37 | 0,13 | 0,05 | 0,018 | 0,007 | 0,002 | 0,001 | |
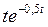
| 1,47 | 1,08 | 0,6 | 0,3 | 0,13 | 0,06 | 0,03 | |
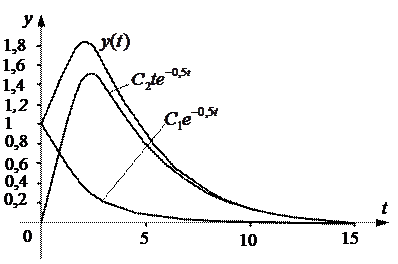 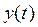
| 1,84 | 1,21 | 0,65 | 0,318 | 0,137 | 0,062 | 0,031 |
3) комплексные сопряженные.
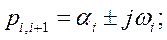
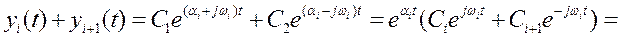
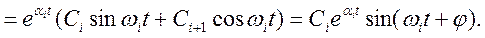
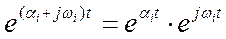
Пример. 1
Дано характеристическое уравнение 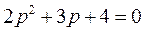 ,
,
n=2,
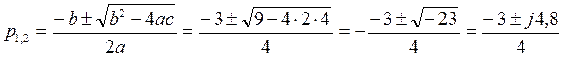
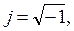
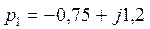 ,
, 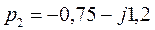 ,
,
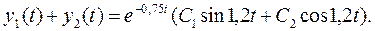 (Затухающие колебания)
(Затухающие колебания)
Пусть С1=1; С2=2, тогда
| t | ||||||
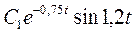
| 0,44 | 0,15 | -0,047 | -0,05 | -0,007 | |
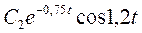
| 0,34 | -0,33 | -0,19 | 0,009 | 0,045 | |
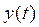
| 0,78 | -0,173 | -0,237 | -0,041 | 0,038 |
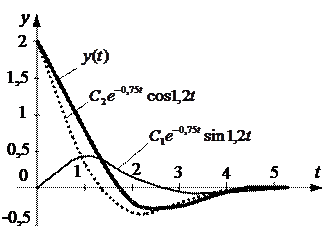
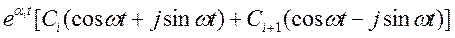
4) мнимые.
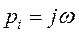 ,
, 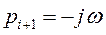 ,
,
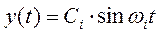 ,
,
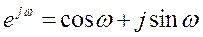 - формула Эйлера.
- формула Эйлера.
Пример. 1
Дано характеристическое уравнение 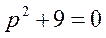 ,
,
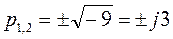 ,
,
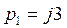 ,
, 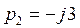 ,
,
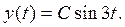 (Незатухающие колебания)
(Незатухающие колебания)
Пусть С=1 , тогда
| t | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | |||||
| Csin3t | 0,14 | -0,98 | -0,28 | 0,94 | 0,41 | -0,88 | -0,54 | 0,8 |
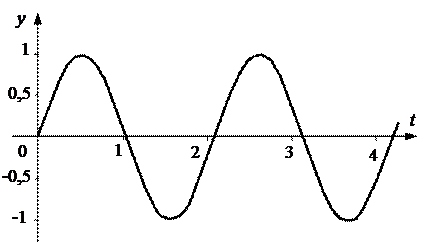
5) комбинации корней.
Пример.1
Дано характеристическое уравнение 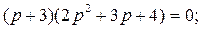 n=3,
n=3,
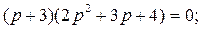
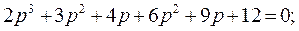
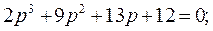 (
( 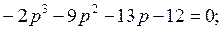 )
)
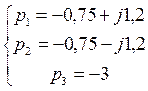 ,
,
2 – комплексно-сопряженных,
1-действительный,
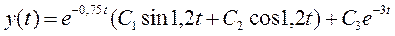 .
.
| t | ||||||
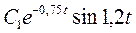
| 0,44 | 0,15 | -0,047 | -0,05 | -0,007 | |
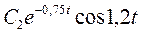
| 0,34 | -0,33 | -0,19 | 0,009 | 0,045 | |
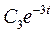
| 0,15 | 0,007 | ||||
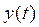
| 1,93 | -0,173 | -0,237 | -0,041 | 0,038 |
| <== предыдущая лекция | | | следующая лекция ==> |
| Вторая форма записи. | | | Порядок построения годографа |
Дата добавления: 2019-10-16; просмотров: 1033;
