Порядок построения годографа

Частотные критерии устойчивости

Частотные критерии позволяют сравнительно легко исследовать устойчивость систем высокого порядка и дают представления о качестве процесса регулирования.

Частотные критерии используют понятие годографа, т.е. кривой в плоскости с координатами 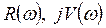(действительная и мнимые части АФЧХ), которую описывает конец вектора 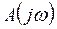при увеличении частоты 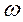от 0 до .

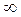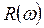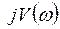Значения и получают, заменив в характеристическом уравнении (2) постоянную p на переменную .

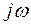Характеристическое уравнение представляет собой полином знаменателя передаточной функции замкнутой САР, т.е.

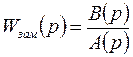
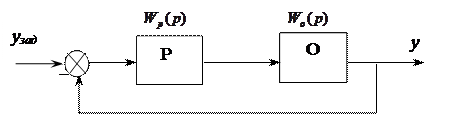Записать передаточные функции разомкнутой и замкнутой САР. Например: регулятор – П (пропорциональный), объект – А (апериодическое звено).

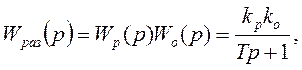
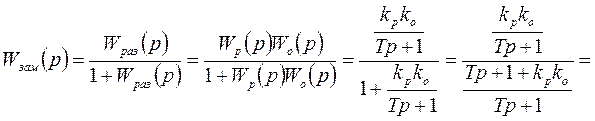
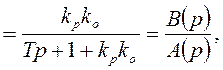
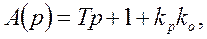
Записываем характеристическое уравнение

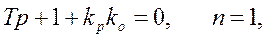
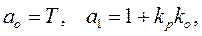
Заменяем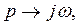

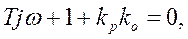
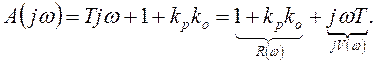
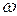
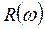
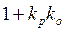
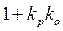
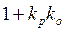
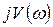
		T	2T

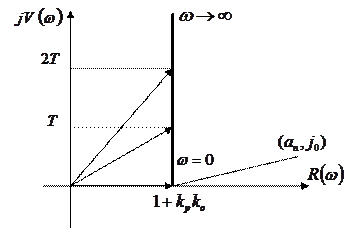Критерий Михайлова

Линейная система n-го порядка устойчива, если при изменении 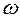от 0 до 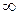годограф Михайлова - 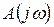последовательно обходит n - квадрантов комплексной плоскости против часовой стрелки, начинаясь в точке 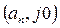на положительной вещественной полуоси и нигде не проходя через начало координат.

Чем дальше годограф от нуля, тем система более устойчива.

Порядок построения годографа

1. Откладывается точка 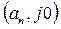при .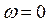

2. Увеличивается частота и находятся другие точки.

3. Определяются точки пересечения с осями координат, как корни уравнений: ,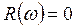

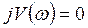
Особенности годографа устойчивых систем

1. Начало в точке , .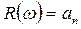

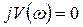2. При 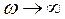вектор 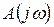поворачивается против часовой стрелки на угол 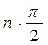, поочередно обходя n - квадрантов.

3. Модуль вектора должен быть отличен от нуля при любых .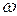

Если годограф проходит через начало координат, то система находится на границе устойчивости.

Пример. 1

Пусть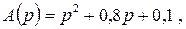

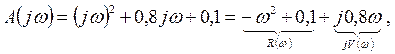
Найдем точки пересечения с осями координат.

С мнимой осью из уравнения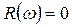

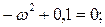
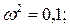
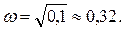Подставив значение 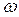в мнимую часть, получим точку пересечения с 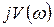(0;0,26).

С действительной осью 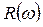из уравнения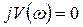

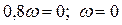. Подставив значение 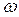в действительную часть, получим точку пересечения с 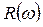(0,1;0).

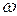
		0,32	0,5		1,25
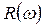
	0,1		-0,15	-0,9	-1,46
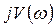
		0,26	0,4	0,8

Система устойчива

Пример. 2

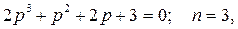
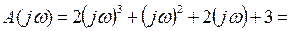
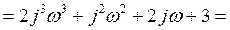
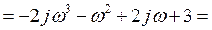
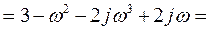
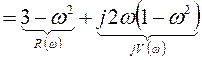
Найдем точки пересечения с осями координат.

С мнимой осью 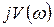из уравнения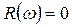

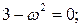
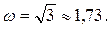Подставив значение 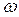в мнимую часть, получим точку пересечения с 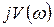(0;-6,8).

С действительной осью 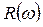из уравнения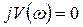

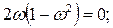
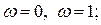Подставив значение 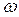в действительную часть, получим точки пересечения с 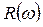(3,0) и (2,0)

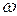
		0,5		1,73
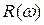
		2,75			-1
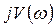
		0,75		-6,8	-12

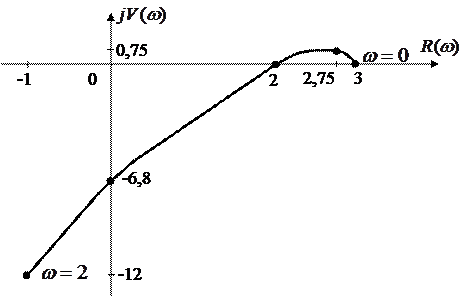
Система неустойчива