Область применения частотных критериев

Критерий Найквиста

Устойчивость определяется по АФЧХ разомкнутой САР. Для разомкнутой САР могут быть 2 случая: устойчивая и неустойчивая.

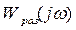1) Разомкнутая САР, устойчивая в разомкнутом состоянии, будет устойчива и в замкнутом состоянии, если ее АФЧХ не охватывает точку (-1;j0), при изменении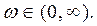

Пример.1

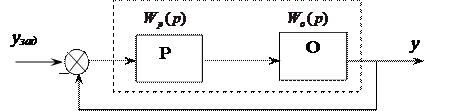
Регулятор – П (пропорциональный),

объект – А (апериодическое звено).

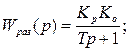
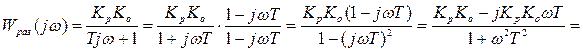
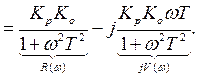
Пусть 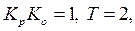тогда

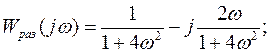
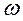
		0,1	0,25	0,5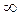
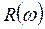
		0,96	0,8	0,5	0,2	0,06	0,027
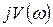
		-0,19	-0,4	-0,5	-0,4	-0,24	-0,16

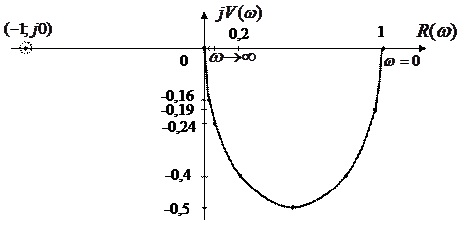
Система устойчива

Пример.2

Регулятор – П (пропорциональный),

объект второго порядка.

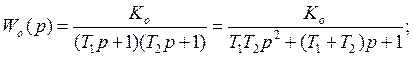
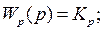
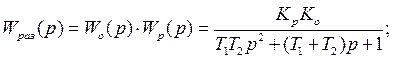
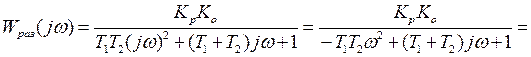
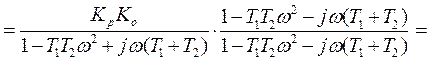
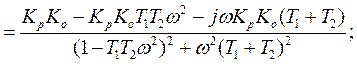
Пусть 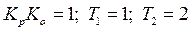тогда

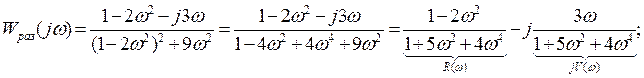
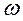
		0,1	0,25	0,5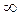
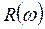
		0,93	0,66	0,2	-0,1	-0,08
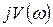
		-0,29	-0,56	-0,6	-0,3	-0,07

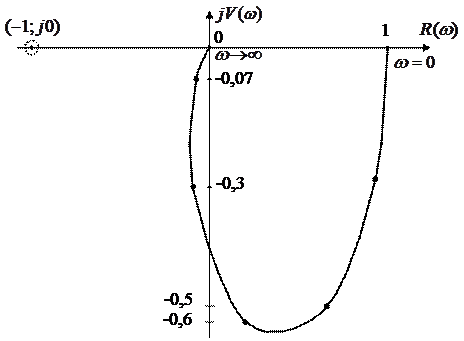Система устойчива

2) Разомкнутая САР, неустойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если АФЧХ 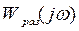охватывает точку (-1;j₀), при изменении 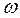от 0 до 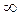против часовой стрелки q раз. Где q - число корней характеристического уравнения разомкнутой САР с положительной вещественной частью.

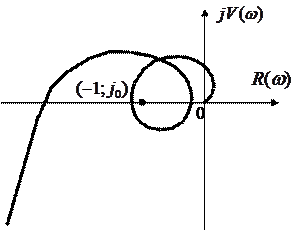Например q=2:

Система устойчива

Если АФЧХ разомкнутой САР 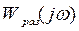проходит через точку (-1;j₀), то замкнутая САР находится на границе устойчивости.

Область применения частотных критериев

1. Критерий Михайлова удобно применять, когда передаточная функция САР задана аналитически.

2. Критерий Найквиста удобно использовать, если АФЧХ разомкнутой САР определена экспериментально.