Молекулярная теория явлений переноса в газах.
Пусть величина 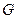 характеризует какое-либо молекулярное свойство отнесенное к одной молекуле: энергию, импульс, концентрацию, заряд, … Имеется градиент
характеризует какое-либо молекулярное свойство отнесенное к одной молекуле: энергию, импульс, концентрацию, заряд, … Имеется градиент 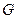 . Сравним потоки с разных сторон произвольно выбранной площадки
. Сравним потоки с разных сторон произвольно выбранной площадки 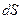 за время
за время 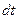 .
.
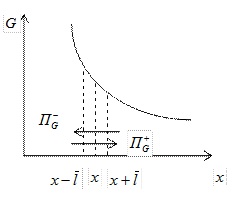
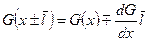 , т.к. обычно
, т.к. обычно 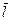 - средняя длина свободного пробега очень мала, то ничего не успевает существенно измениться.
- средняя длина свободного пробега очень мала, то ничего не успевает существенно измениться.
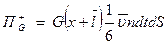 ,
, 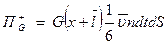
- 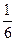 т.к. все направления равновероятны и в среднем
т.к. все направления равновероятны и в среднем 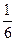 часть всех молекул двигается в одном направлении.
часть всех молекул двигается в одном направлении.
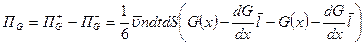
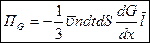 .
.
Мы получили основное уравнение переноса параметра 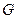 - поток параметра через площадку
- поток параметра через площадку 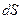 за время
за время 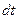 . Плотность потока параметра через единичную площадку в единицу времени:
. Плотность потока параметра через единичную площадку в единицу времени:
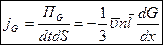 .
.
Получим выражения для расчетов коэффициентов переноса – коэффициента теплопроводности, коэффициента диффузии, динамической вязкости, который входили в экспериментально полученные законы переноса.
1) Теплопроводность. В данном случае переносится энергия теплового движения.
В качестве параметра возьмем среднюю энергию теплового движения 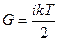 .
.
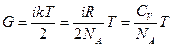 , тогда переносимое количество теплоты с учетом закона Фурье
, тогда переносимое количество теплоты с учетом закона Фурье
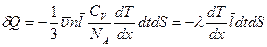 , для коэффициента теплопроводности получим:
, для коэффициента теплопроводности получим:
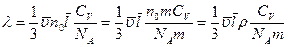 , здесь
, здесь 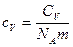 - удельная теплоемкость,
- удельная теплоемкость, 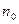 - равновесная концентрация,
- равновесная концентрация, 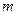 - масса молекулы.
- масса молекулы.
Окончательно имеем для коэффициента теплопроводности: 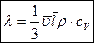
2) Диффузия. В данном случае переносится вещество из области с большей концентрацией в область с меньшей концентрацией. В качестве параметра возьмем отношение концентраций в процентах к равновесной концентрации 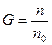 .
.
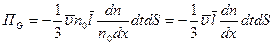 .
.
Переносимое количество вещества по закону Фика 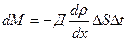 , тогда умножив на массу молекулы поток изменения концентрации, получим переносимую массу:
, тогда умножив на массу молекулы поток изменения концентрации, получим переносимую массу:
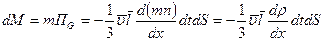 , учтем закона Фика, записав равенство для соответствующих множителей.
, учтем закона Фика, записав равенство для соответствующих множителей.
Окончательно для коэффициента диффузии получим: 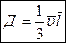 .
.
3) Вязкость. В данном случае переносится количество движения, импульс вещества из области с большей скоростью движения молекул в область с меньшей скоростью. В качестве переносимого параметра возьмем импульс одной молекулы 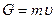 . Тогда переносимый поток
. Тогда переносимый поток
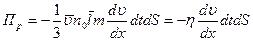 , с учетом закона Ньютона.
, с учетом закона Ньютона.
Окончательно для коэффициента динамической вязкости: 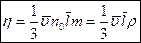 .
.
Между коэффициентами переноса существует связь, которая является свидетельством одинаковых механизмов переноса.
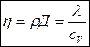 .
.
Дата добавления: 2019-10-16; просмотров: 504;
