Логические основы ЭВМ

Введение

В основе всех действий, произведенных компьютером, лежат логические выводы основанные на булевой логике. С появлением транзисторов началось второе поколение ПК, и далее на этой основе развивались следующие поколения.

Сейчас широко используется транзисторная логика для построения булевой логики в вычислительной технике. В основе всего лежат транзисторы, логические элементы, триггеры и т.д. Любая интегральная схема строится с использованием триггеров и логических элементов, на основе которых можно построить схему любой сложности.

6.1. Бистабильная ячейка – триггер

Триггер — это электронная схема, широко применяемая в регистрах компьютера для надежного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю.

Термин триггер происходит от англ. trigger — защелка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает «хлопанье». Это звукоподражательное название электронной схемы указывает на ее способность почти мгновенно переходить («перебрасываться») из одного электрического состояния в другое и наоборот.

Самый распространенный тип триггера — так называемый RS-триггер (S и R, соответственно, от англ. set — установка, reset — сброс). Условное обозначение триггера дано на рис. 6.1.

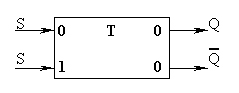
Рис. 6.1. Условное обозначение триггера

Он имеет два симметричных входа S и R и два симметричных выхода Q и 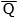, причем выходной сигнал Q является логическим отрицанием сигнала .

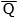На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов ( ).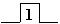

Наличие импульса на входе будем считать единицей, а его отсутствие — нулем.

На рис. 6.2 показана реализация триггера с помощью вентилей ИЛИ-НЕ, соответствующая таблица истинности приведена в табл. 6.1.

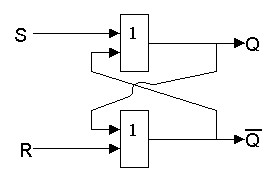
Рис. 6.2. Реализация триггера с помощью вентилей ИЛИ-НЕ

Таблица 6.1. Таблица истинности триггера

S	R	Q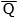
		Запрещено
		Хранение бита

Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ-НЕ (табл. 6.1).

1. Если на входы триггера подать S=1, R=0, то (независимо от состояния) на выходе Q верхнего вентиля появится 0. После этого на входах нижнего вентиля окажется R=0, Q=0 и выход 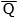станет равным 1.

2. Точно так же при подаче 0 на вход S и 1 на вход R на выходе 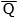появится 0, а на Q — 1.

3. Если на входы R и S подана логическая 1, то состояние Q и 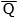не меняется.

4. Подача на оба входа R и S логического 0 может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена.

Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания 1 байта нужно 8 триггеров, для запоминания 1 Кбайта — соответственно 8 · 210 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.

Регистры

Регистрами называют устройства, предназначенные для приема, хранения и передачи информации.

Информация в регистре хранится в виде двоичного кода, каждому разряду которого соответствует свой элемент памяти (разряд регистра), выполненный на основе триггеров RS-, JK- или D-типа.

Классифицировать регистры можно по различным признакам, важнейшими из которых являются способ ввода-вывода информации и характер представления вводимой и выводимой информации.

По способу ввода-вывода информации различают параллельные, последовательные и параллельно-последовательные регистры. В регистрах памяти и ввод информации и ее вывод осуществляются в параллельном коде. При этом время ввода (вывода) всего числа равно времени ввода (вывода) одного разряда. В регистрах сдвига число вводится и выводится последовательно разряд за разрядом. Время ввода (вывода)m-разрядного двоичного числа в таких регистрах определяется величиной mT_c, где T_c — период следования тактовых импульсов, осуществляющих ввод (вывод) информации. В параллельно-последовательном регистре ввод числа может осуществляться в параллельном коде, а вывод — в последовательном или наоборот.

По характеру представления вводимой и выводимой информации различают регистры однофазного и парафазного типов. В однофазных регистрах информация вводится в прямом либо в обратном коде, а в парафазных — одновременно и в прямом, и в обратном. Регистры первого типа строятся на основе D-триггеров, второго — на основе RS- или JK-триггеров. Вывод информации из регистров обоих типов может осуществляться в прямом и в обратном кодах.

Сумматор

Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел.

Сумматор служит прежде всего центральным узлом арифметико-логического устройства компьютера, однако его применяют и в других устройствах машины.

Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров, с рассмотрения которых мы и начнём. Условное обозначение одноразрядного сумматора дано на рис. 6.3.

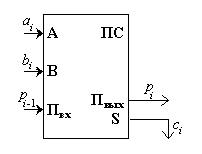
Рис. 6.3. Условное обозначение одноразрядного сумматора

При сложении чисел A и B в одном i-м разряде приходится иметь дело с тремя цифрами:

1. цифра a_i первого слагаемого;

2. цифра b_i второго слагаемого;

3. перенос p_i–1 из младшего разряда.

В результате сложения получаются две цифры:

1. цифра ci для суммы;

2. перенос p_i из данного разряда в старший.

Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана соответствующей таблицей истинности (табл. 6.2).

Таблица 6.2. Таблица истинности одноразрядного двоичного сумматора

Если требуется складывать двоичные слова длиной 2 бита и более, то можно использовать последовательное соединение таких сумматоров, причем для двух соседних сумматоров выход переноса одного сумматора служит входом для другого.

Например, схема вычисления суммы C = (с₃ c₂ c₁ c₀) двух двоичных трехразрядных чисел A = (a₂ a₁ a₀) и B = (b₂ b₁ b₀) может иметь вид, показанный на рис. 6.4.

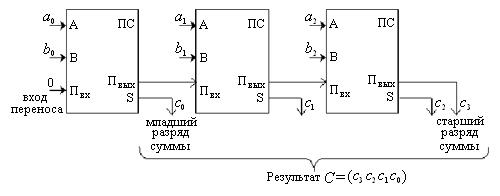
Рис. 6.4. Схема вычисления суммы двух двоичных трёхразрядных чисел