Кодирование графической информации
Под графической информацией можно понимать рисунок, чертеж, фотографию, картинку в книге, изображения на экране телевизора или в кинозале и т. д. Рассмотрим принципы кодирования графической информации на примере изображения на экране телевизора. Это изображение состоит из горизонтальных линий — строк, каждая из которых в свою очередь состоит из элементарных мельчайших единиц изображения — точек, которые принято называть пикселями (picsel — PICture'S ELement — элемент картинки). Весь массив элементарных единиц изображения называют растром.
Степень четкости изображения зависит от количества строк на весь экран и количества точек в строке, которые представляютразрешающую способность экрана, или просто разрешение. Чем больше строк и точек, тем четче и лучше изображение.
Если мы посмотрим на показатели разрешения современных плазменных и жидкокристаллических телевизоров, то обнаружим, что наиболее распространенные разрешения – 640×480 (ЖК-телевизоры с соотношением сторон 4:3); 852×480 (плазменные панели с соотношением сторон 16:9), 1024×768 (ЖК и «плазма» как 4:3, так и 16:9); 1366×768 (HD Ready); 1920×1080 (Full HD) пикселей. Встречаются, но редко, и некоторые другие значения разрешения, например 800×600 или 1024×1024 пикселей.
Обозначение разрешения, например 640×480, означает, что используется 480 горизонтальных строк по 640 пикселей в каждой. Таким образом, изображение на экране представляет собой последовательность из 640·480=307200 пикселей.
Изображения могут быть монохромными и цветными.
Монохромное изображение состоит из любых двух контрастных цветов — черного и белого, зеленого и белого, коричневого и белого и т. д. Для простоты обсуждения будем считать, что один из цветов — черный, а второй — белый. Тогда каждый пиксель изображения может иметь либо черный, либо белый цвет. Поставив в соответствие черному цвету двоичный код «0», а белому — код «1» (либо наоборот), мы сможем закодировать в 1 бите состояние 1 пикселя монохромного изображения. Однако полученное таким образом изображение будет чрезмерно контрастным.
Общепринятым на сегодняшний день, дающим достаточно реалистичные монохромные изображения, считается кодирование состояния 1 пикселя с помощью 1 байта, которое позволяет передавать 256 различных оттенков серого цвета от полностью белого, до полностью черного. В этом случае для передачи всего растра из 640×480 пикселей потребуется 307200 байт.
Цветное изображение может формироваться на основе различных моделей. Наиболее распространенные цветовые модели:
· RGB чаще всего используется в информатике;
· CMYK — основная цветовая модель в полиграфии;
· в телевидении для стандарта PAL применяется цветовая модель YUV, для SÉCAM — модель YDbDr, а для NTSC — модель YIQ;
· эталонная модель XYZ основана на замерах характеристик человеческого глаза.
Модель RGB (от слов Red, Green, Blue — красный, зеленый, синий) наиболее точно подходит к принципам вывода изображения на экран монитора – три числа задают яркость свечения зерен красного, зеленого и синего люминофора в заданной точке экрана. Поэтому данная модель получила наиболее широкое распространение в области компьютерной графики, ориентированной на просмотр изображений на экране монитора.
Модель RGB опирается на то, что глаз человека воспринимает все цвета как сумму трех основных цветов — красного, зеленого и синего(рис.4.1). Так как цвет формируется в результате сложения трех цветов, эту модель часто называют аддитивной (суммирующей).
Например, для задания белого цвета необходимо указать для всех трех компонентов максимальные значения яркости, а для задания черного – полностью погасить все источники (например, точки люминофора), задающие цвет в нужной точке изображения, – указать для них нулевую яркость.
Если каждый из цветов кодировать с помощью 1 байта (яркость каждого компонента задается числами от 0 до 255), как это принято для реалистического монохромного изображения, появится возможность передавать по 256 оттенков каждого из основных цветов. А всего в этом случае обеспечивается передача 256 · 256 · 256 = 16 777 216 различных цветов, что достаточно близко к реальной чувствительности человеческого глаза. Таким образом, при данной схеме кодирования цвета на изображение 1 пикселя требуется 3 байта или 24 бита памяти. Этот способ представления цветной графики принято называть режимом True Color (true color — истинный цвет) или полноцветным режимом.
Существуют профессиональные устройства (например, сканеры), позволяющие получать изображения, в которых каждый пиксел описывается не тремя, а шестью (16 бит на каждую цветовую составляющую) или даже восемью байтами. Подобные режимы используются для наилучшей передачи оттенков и, что самое главное, яркости точек изображения. Это позволяет наиболее достоверно воспроизводить изображения таких сложных с технической точки зрения сюжетов, как, например, вечерние или рассветные пейзажи.
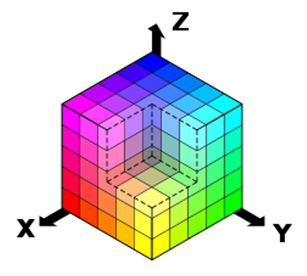
Рис. 4.1. RGB-цветовая модель, представленная в виде куба
Пример 4.7. В Win32 стандартный тип для представления цветов – COLORREF. Для определения цвета в RGB используется 4 байта в виде:
0×00BBGGRR
BB, GG, RR — значение интенсивности соответственно синей, зеленой и красной составляющих цвета. Максимальное их значение — 0xFF.
Тогда определить переменную типа COLORREF можно следующим образом:
COLORREF C = (b,g,r);
b, g и r — интенсивность (в диапазоне от 0 до 255) соответственно синей, зеленой и красной составляющих определяемого цвета C. То есть ярко-красный цвет может быть определен как (255,0,0), ярко-фиолетовый — (255,0,255), черный — (0,0,0), а белый — (255,255,255).
Полноцветный режим требует много памяти. Поэтому памяти разрабатываются различные режимы и графические форматы, которые немного хуже передают цвет, но требуют гораздо меньше памяти. В частности, можно упомянуть режим High Color (high color — богатый цвет), в котором для передачи цвета 1 пикселя используется 16 бит, и, следовательно, можно передать 65 535 цветовых оттенков, а также индексный режим, который базируется на заранее созданной для данного рисунка таблице используемых в нем цветовых оттенков. Затем нужный цвет пикселя выбирается из этой таблицы с помощью номера — индекса, который занимает всего 1 байт памяти. При записи изображения в память компьютера, кроме цвета отдельных точек, необходимо фиксировать много дополнительной информации — размеры рисунка, разрешение, яркость точек и т. д. Конкретный способ кодирования всей требуемой при записи изображения в память компьютера информации образует графический формат. Форматы кодирования графической информации, основанные на передаче цвета каждого отдельного пикселя, из которого состоит изображение, относят к группе растровых, или BMP (Bit MaP — битовая карта), форматов [1].
Модель CMYK(Cyan, Magenta, Yellow, blacK) субтрактивная схема формирования цвета, используемая прежде всего в полиграфии для стандартной триадной печати. Схема CMYK (рис. 4.2), как правило, обладает сравнительно небольшим цветовым охватом [3].
Рис. 4.2. Схема субтрактивного синтеза в CMYK
По-русски эти цвета часто называют так: голубой, пурпурный, жёлтый. Цвет в такой схеме зависит не только от спектральных характеристик красителей и от способа их нанесения, но и их количества, характеристик бумаги и других факторов. Например, есть американский, европейский и японский стандарты для мелованной и немелованной бумаг.
Хотя теоретически черный цвет можно получать смешением в равной пропорции пурпурного, голубого и желтого, на практике смешение реальных пурпурного, голубого и желтого цветов дает скорее грязно-коричневый или грязно-серый цвет. Так как чистота и насыщенность черного цвета чрезвычайно важны в печатном процессе, в модель был введен ещё один цвет – черный.
Объяснение первых трех букв в аббревиатуре CMYK дано выше, а по поводу четвертой одна из версий утверждает, что K – сокращение от англ. blacK (если бы взяли B, то возникла бы путаница с моделью RGB, где B – это синий цвет). Согласно этой версии, при выводе полиграфических пленок на них одной буквой указывался цвет, которому они принадлежат. Согласно другому варианту, буква K появилась от сокращения англ. слова Key: в англоязычных странах термином key plate обозначается печатная форма для черной краски.
CMYK называют субтрактивной моделью, потому что эту модель применяют в основном в полиграфии при цветной печати, а бумага и прочие печатные материалы служат поверхностями, отражающими свет: удобнее считать, какое количество света (и цвета) отразилось от той или иной поверхности, нежели – сколько поглотилось. Таким образом, если вычесть из белого три первичных цвета, RGB, мы получим тройку дополнительных цветов CMY. «Субтрактивный» означает «вычитаемый» – мы вычитаем первичные цвета из белого.
Каждое из чисел, определяющее цвет в CMYK, представляет собой процент краски данного цвета, составляющей цветовую комбинацию, Например, для получения темно-оранжевого цвета следует смешать 30 % голубой краски, 45 пурпурной, 80 желтой и 5 % черной краски. Это можно обозначить следующим образом: (30,45,80,5). Иногда пользуются таким обозначением: C30M45Y80K5.
Контрольные вопросы и задания
1. Что называется форматом данных?
2. Как в компьютерах кодируется числовая информация?
3. Как связан диапазона представления целого числа с форматом его хранения.
4. Есть ли различия в отображении положительных чисел в прямом, обратном и дополнительном кодах?
5. Представьте число -78 в прямом, обратном и дополнительном кодах в однобайтовом формате.
6. Как связаны точность и диапазон представления вещественного числа с разрядностью мантиссы?
7. Почему порядок при представлении вещественного числа называют смещенным?
8. Почему при представлении нормализованного вещественного числа не хранят первую цифру мантиссы?
9. Представьте число 34.256 в одинарном формате вещественного числа.
10. Как в компьютерах кодируется текстовая информация?
11. Для чего используются кодовые таблицы? Какие кодовые таблицы вам известны?
12. Чем отличаются базовая таблица ASCII от расширенной?
13. Какие преимущества дает представление текстовой информации в формате Юникод?
14. Дайте определения понятиям пиксель, растр, разрешающая способность .
15. Сколько байт памяти необходимо, чтобы закодировать изображение на экране компьютерного монитора с разрешением 800×600 при 256 цветах?
16. Какие модели формирования цветных изображений вам известны?
17. Какие цвета считаются основными в моделях RGB и CMYK?
5. Основные понятия алгебры логики
5.1. Логические величины: истина (логическая единица) и ложь (логический ноль)
Принципы работы ЭВМ основываются на законах математической логики, поскольку компьютеры — это автоматические устройства, чья работа базируется на элементарных законах двоичной логики.
Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Основное понятие алгебры логики — высказывание.
Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.
Например, высказывание «Земля — это планета Солнечной системы» ИСТИННО, а о высказывании «На улице идет дождь» можно сказать, истинно оно или ложно, если указаны дополнительные сведения о погоде в данный момент.
Любое высказывание можно обозначить символом х и считать, что х = 1, если высказывание истинно, а х = 0, если высказывание ложно.
Логическая {булева) переменная — такая величина х, которая может принимать только два значения: х = {0,1}.
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Разумеется, не всякое предложение можно считать логическим высказыванием. Высказываниями не являются, например, предложения «Ученик десятого класса» и «Информатика — интересный предмет». Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределенное понятие «интересный предмет». Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.
5.2. Логические операции: инверсия, дизъюнкция и конъюнкция
Алгебра логики рассматривает любое высказывание только с одной точки зрения — истинно оно или ложно.
Заметим, что зачастую трудно установить истинность высказывания. Так высказывание «Площадь поверхности Индийского океана равна 75 млн км2» в одной ситуации можно считать ложным, а в другой — истинным. Ложным — так как указанное значение неточное и вообще не постоянное. Истинным — если рассматривать его как некоторое приближение, приемлемое на практике.
Употребляемые в обычной речи слова и словосочетания не, и, или, если... , то, тогда и только тогда и др. позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Bысказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Так из элементарных высказываний «Петров — врач», «Петров — шахматист» при помощи связки и можно получить составное высказывание «Петров — врач и шахматист», понимаемое как «Петров — врач, хорошо играющий в шахматы».
При помощи связки или из этих же высказываний можно получить составное высказывание «Петров — врач или шахматист», понимаемое в алгебре логики как «Петров или врач, или шахматист, или и врач и шахматист одновременно».
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:
НЕ. Операция, выражаемая этим словом, называется отрицанием и обозначается чертой над высказыванием (или знаком  ).
).
Высказывание 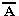 истинно, когда A ложно, и ложно, когда A истинно. Например, «Луна — спутник Земли» (А); «Луна — не спутник Земли» (
истинно, когда A ложно, и ложно, когда A истинно. Например, «Луна — спутник Земли» (А); «Луна — не спутник Земли» ( 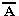 ).
).
Схема НЕ (инвертор) реализует операцию отрицания.
Если на входе схемы 0, то на выходе 1; если на входе 1, на выходе 0. Условное обозначение инвертора — на рис. 5.1, а таблица истинности — в табл. 5.1.
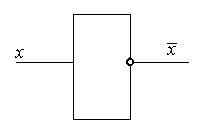
Рис. 5.1. Условное обозначение инвертора
Талица 5.1. Таблица истинности инвертора
| А | Не А |
| Да (1) | Нет (0) |
| Нет (0) | Да (1) |
И. Операция, выражаемая этой связкой, называется конъюнкцией (лат. conjunctio — соединение), или логическим умножением, и обозначается точкой « . » (может также обозначаться знаками ^ или &).
Высказывание А · В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание «10 делится на 2 и 5 больше 3» истинно, а высказывания «10 делится на 2 и 5 не больше 3», «10 не делится на 2 и 5 больше 3», «10 не делится на 2 и 5 не больше 3» — ложны.
Схема И реализует конъюнкцию двух или более логических значений.
Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 5.2, таблица истинности конъюнкции — в табл. 5.2.
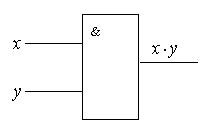
Рис. 5.2. Условное обозначение схемы И с двумя входами
Талица 5.2. Таблица истинности схемы И с двумя входами
| А | В | А и В |
| Да (1) | Да (1) | Да (1) |
| Да (1) | Нет (0) | Нет (0) |
| Нет (0) | Да (1) | Нет (0) |
| Нет (0) | Нет (0) | Нет (0) |
ИЛИ. Операция, выражаемая этой связкой (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v (или плюсом).
Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание «10 не делится на 2 или 5 не больше 3» ложно, а высказывания «10 делится на 2 или 5 больше 3», «10 делится на 2 или 5 не больше 3», «10 не делится на 2 или 5 больше 3»— истинны.
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.
Условное обозначение схемы ИЛИ представлено на рис. 5.3, таблица истинности — в табл. 5.3.
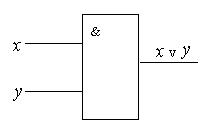
Рис. 5.3. Условное обозначение схемы ИЛИ с двумя входами
Талица 5.3. Таблица истинности схемы ИЛИ с двумя входами
| А | В | А или В |
| Да (1) | Да (1) | Да (1) |
| Да (1) | Нет (0) | Да (1) |
| Нет (0) | Да (1) | Да (1) |
| Нет (0) | Нет (0) | Нет (0) |
Операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (НЕ), затем конъюнкция (И), после конъюнкции — дизъюнкция (ИЛИ) и в последнюю очередь — импликация.
Дата добавления: 2019-10-16; просмотров: 697;
