Методы и алгоритмы анализа на макроуровне

Выбор методов анализа во временной области.Анализ процессов в проектируемых объектах можно производить во временной и частотной областях. Анализ во временной области (динамический анализ) позволяет получить картину переходных процессов, оценить динамические свойства объекта, он является важной процедурой при исследовании как линейных, так и нелинейных систем. Анализ в частотной области более специфичен, его применяют, как правило, к объектам с линеаризуемыми ММ при исследовании колебательных стационарных процессов, анализе устойчивости, расчете искажений информации, представляемой спектральными составляющими сигналов, и т.п.

Методы анализа во временной области, используемые в универсальных программах анализа в САПР, – это численные методы интегрирования систем обыкновенных дифференциальных уравнений (СОДУ):

F(dV/dt, V, t) = 0.

Другими словами, это методы алгебраизации дифференциальных уравнений. Формулы интегрирования СОДУ могут входить в ММ независимо от компонентных уравнений, как это имеет место в (3.15), или быть интегрированными в ММ компонентов, как это выполнено в узловом методе.

От выбора метода решения СОДУ существенно зависят такие характеристики анализа, как точность и вычислительная эффективность. Эти характеристики определяются прежде всего типом и порядком выбранного метода интегрирования СОДУ.

Применяют два типа методов интегрирования – явные (иначе экстраполяционные или методы, основанные на формулах интегрирования вперед), и неявные (интерполяционные, основанные на формулах интегрирования назад). Различия между ними удобно показать на примере простейших методов первого порядка – методов Эйлера.

Формула явного метода Эйлера представляет собой следующую формулу замены производных в точке t_n:

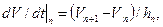
где индекс равен номеру шага интегрирования; h_n=t_n+1–t_n – размер шага интегрирования (обычно h_n называют просто шагом интегрирования). В формуле неявного метода Эйлера использовано дифференцирование назад:

где h_n=t_n – t_n-1.

Выполним сравнительный анализ явных и неявных методов на примере модельной задачи:

dV/dt = AV(3.23)

при ненулевых начальных условиях V₀≠0 и при использовании методов Эйлера с постоянным шагом h. Здесь А – постоянная матрица; V – вектор фазовых переменных.

При алгебраизации явным методом имеем

(V_n+1-V_n)/h=AV_n

или

V_n+1 = (Е + hA) V_n

где Е – единичная матрица. Вектор V_n+1 можно выразить через вектор начальных условий V₀:

V_n+1 = (Е + hA)ⁿ V₀ (3.24)

Обозначим

В = Е + hА (3.25)

и применим преобразование подобия для матрицы В

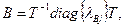
где Т – преобразующая матрица, 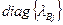-диагональная матрица с собственными значениями -матрицы В на диагонали. Нетрудно видеть, что

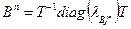
Из линейной алгебры известно, что собственные значения матриц, связанных арифметическими операциями, оказываются связанными такими же преобразованиями. Поэтому из (3.25) следует

λ_Bj = 1 + hλ_Aj

Точное решение модельной задачи (3.23) V(t)→ 0 при t →∞, следовательно, условием устойчивости процесса численного решения можно считать

V_n+1→ 0 при t →∞

откуда последовательно получаем

(Е + hA)ⁿ V₀→ 0,

так как V₀ ≠ 0, то (Е + hA)ⁿ → 0, поскольку Т ≠ 0, 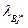→ 0 и условие устойчивости

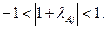(3.26)

Известно, что для физически устойчивых систем собственные значения матрицы коэффициентов в ММС оказываются отрицательными. Если к тому же все , вещественные величины (характер процессов в ММС с моделью (3.23) апериодический), то естественно определить постоянные времени физической системы как

τ_j = -1 / λ_Aj,

и условие (3.26) конкретизируется следующим образом

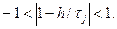
или

0 < h <2τ_min (3.27)

где 2τ_min – минимальная постоянная времени. Если использовать явные методы более высокого порядка, то может увеличиться коэффициент перед 2τ_min в (3.27), но это принципиально не меняет оценки явных методов.

Если нарушено условие (3.27), то происходит потеря устойчивости вычислений, а это означает, что в решении задачи возникают ложные колебания с увеличивающейся от шага к шагу амплитудой и быстрым аварийным остановом ЭВМ вследствие переполнения разрядной сетки. Конечно, ни о какой адекватности решения говорить не приходится.

Для соблюдения (3.27) применяют те или иные алгоритмы автоматического выбора шага. Отметим, что в сложной модели расчет τ_min для непосредственного выбора шага по (3.27) слишком трудоемок, кроме того, однократный расчет τ_min мало чем помогает, так как в нелинейных моделях τ_min может изменяться от шага к шагу.

Условие (3.27) накладывает жесткие ограничения на шаг интегрирования. В результате вычислительная эффективность явных методов резко падает с ухудшением обусловленности ММС. В самом деле, длительность Т_инт моделируемого процесса должна быть соизмеримой с временем успокоения системы после возбуждающего воздействия, т.е. соизмерима с максимальной постоянной времени τ_max.Требуемое число шагов интегрирования равно

Ш= Т_инт / h ~ τ_max / τ_min.

Отношение Ч = τ_max/τ_min называют разбросом постоянных времени или числом обусловленности. Чем больше это число, тем хуже обусловленность. Попытки применения явных методов к любым ММС чаще всего приводят к недопустимо низкой вычислительной эффективности, поскольку в реальных моделях Ч > 10⁵ – обычная ситуация. Поэтому в настоящее время в универсальных программах анализа явные методы решения СОДУ не применяют.

Аналогичный анализ числовой устойчивости неявных методов дает следующие результаты. Вместо (3.24) имеем

Vn=(Е - hA)^-nV₀

и условие числовой устойчивости принимает вид

,

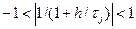которое выполняется при любых h > 0. Следовательно, неявный метод Эйлера обладает так называемой А-устойчивостъю.

Примечание.Метод интегрирования СОДУ называют A-устойчивым, если погрешность интегрирования остается ограниченной при любом шаге h>0.

Применение A-устойчивых методов позволяет существенно уменьшить требуемые числа шагов Ш. В этих методах шаг выбирается автоматически не из условий устойчивости, а только из соображений точности решения.

Выбор порядка метода решения СОДУ довольно прост: во-первых, более высокий порядок обеспечивает более высокую точность, во-вторых, среди неявных разностных методов, кроме метода Эйлера, A-устойчивы также методы второго порядка и среди них – метод трапеций. Поэтому преобладающее распространение в программах анализа получили методы второго порядка – модификации метода трапеций.