Мощность при вращательном движении
Если вал машины передает скручивающий момент Мх, например, от мотора к станку, то значение момента зависит от передаваемой мощности Р и частоты вращения вала. Учитывая, что мощность равна работе в единицу времени 1Вт = 1Нм/с, можно составить равенство
,
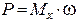где Р – мощность, Вт(кВт);
Мх – момент, Н∙м (кН∙м);
ω – угловая скорость, 1/с: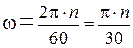 
.
Тогда скручивающий момент Мх определится по формуле
,
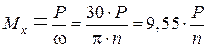где n – число оборотов в минуту, об /мин.
Пример 8
Шкив с диаметром D 1= 1м и с углом наклона ветвей ремня к горизонту
α 1 = 0 o , делает n = 100 об/мин и передаёт мощность P = 100 кВт. Два других шкива имеют одинаковый диаметрD 2= 0,8 м и одинаковые углы наклона ветвей ремней к горизонту α 2 = 60° и каждый из них передает мощность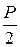 
(риcунок 32, а). Соотношения сил натяжения ремней для шкивов соответственно равны: Т1 = 2t 1 , Т2 = 2t 2 (риcунок 32, з). Требуется подобрать диаметр вала d , если допускаемое напряжение материала вала [ σ ] = 100 МПа..
Решение.
Скручивающие моменты, действующие на вал со стороны шкивов, будут вызывать деформацию кручения вала, а вследствие действия сил натяжения ремней шкивов вал будет подвержен также и деформациям изгиба в вертикальной и горизонтальной плоскостях.
Определяем внешние скручивающие моменты Mк1 и Mк2, вызывающие кручение вала:
Mк1 =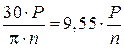 
= 
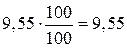кН∙м,
= 
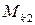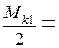4,775 кН∙м.
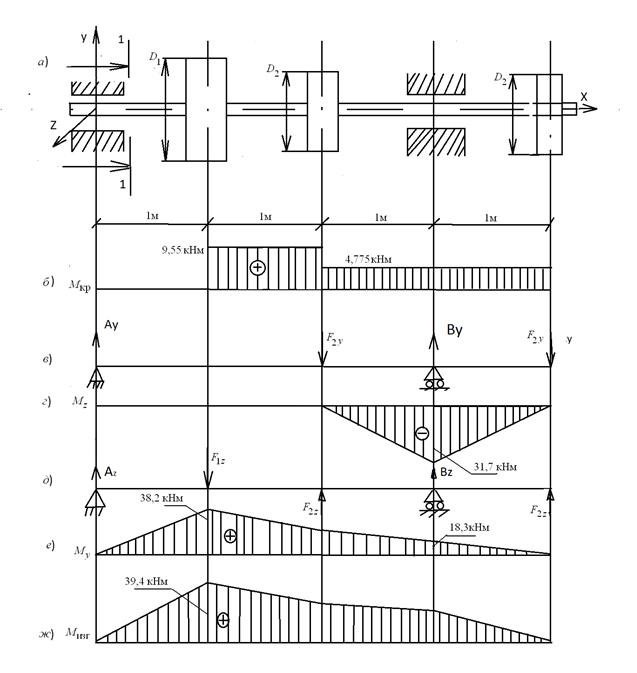
Строим эпюру крутящих моментов Mк (риcунок 32, б).
Определим натяжение ремней t 1 , Т1 = 2t 1 , t 2 , Т2 = 2t 2 :
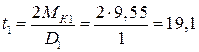кН, 
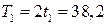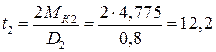кН,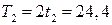
кН, 
кН.
Находим результирующие сосредоточенные силы F1 , F2 :
F1 = (t1 + Т1) = (19,1 + 38,2) = 57,3 кН
F2 = (t2 + Т2) = (12,2 + 24,4) = 36,6 кН
Проектируем силы натяжения ремней F1 и F2, действующие в плоскости каждого шкива, на оси y и z (рисунок 32, з).
F1y = (t1 + Т1) ∙ sinα1 = (19,1 + 38,2) ∙ sin0o = 0,
F1z = (t1 + Т1) ∙ cosα1 = (19,1 + 38,2) ∙ cos0o = 57,3 кН,
F2у = (t2 + Т2) ∙ sinα2 = (12,2 + 24,4) ∙ sin 60o = – 31,7 кН,
F2z = (t2 + Т2) ∙ cosα2 = (12,2 + 24,4) ∙ cos60o = –18,3 кН.
Расчетная схема вала на изгиб в вертикальной плоскости представлена на
рисунке 32, в.
Строим эпюру изгибающих моментов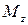 
в вертикальной плоскости
(рисунок 32, г.).
Расчетная схема вала на изгиб в горизонтальной плоскости представлена
на рисунке 32, д.
Строим эпюру изгибающих моментов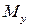 
в горизонтальной плоскости
(рисунок 32, е).
Строим эпюру суммарных изгибающих моментов Миэг (рисунок 32, ж),
пользуясь формулой:
.
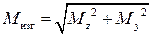Определяем эквивалентный изгибающий момент Мэкв по третьей теории
прочности.
Опасным сечением вала будем сечение, где расположен шкив с диаметром D 1
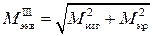
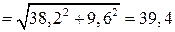кН∙м.
Определяем диаметр вала d из условия прочности
σэкв =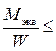 
[σ],
где осевой момент сопротивления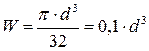 
.
Следовательно: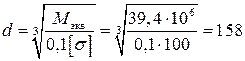 
мм =15,8 см.
Принимаем диаметр вала d =16 см.
з) 1-1
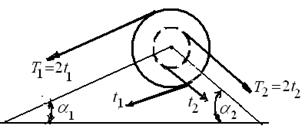
Рисунок 32 − Расчет вала на кручение с изгибом
Задача 10
Дата добавления: 2019-07-26; просмотров: 1064;