Структурный анализ технологических систем механической обработки
| № п/п | Система отсчета
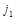 координат координат
| Соотно-шение между j1 и j2 | Эквивалентная схема | Передаточная функция | Структурная схема | Переходная функция |
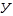 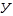 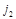 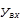 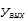 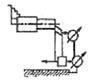
| j1 >> j2 |  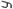   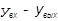 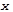 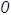 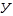 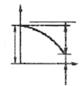
| 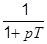 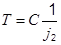
|
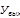 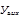 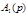 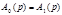 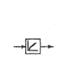 
| 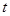 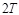 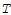  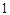 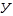 
| |
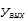 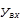 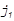 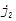 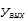 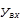 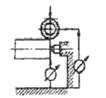
| j2 >> j1 | 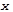 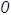 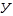 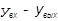     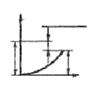
| 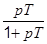 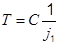
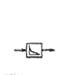
| 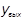 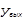 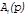 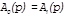 
| 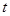 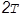 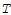  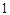 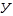 
| |
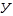 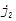 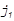 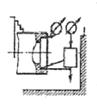
| j1 ≈ j2 | 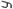  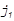 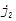 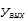 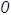 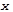 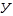 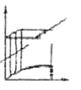
| 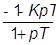 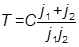 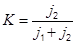
| 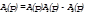 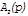 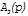  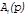 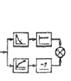
| 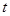 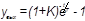 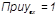 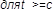    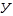 
| |
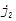 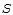 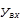 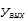 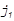 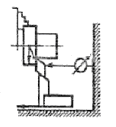
| j1 ≥ j2 | 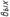 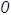  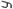 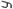 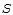 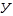 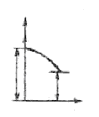
|
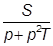
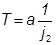
| 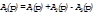 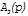 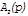 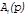 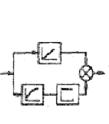
| 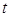 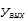 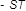  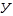 
| |
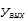 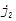 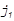 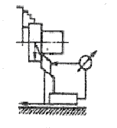
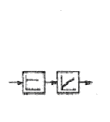
| j1 ≥ j2 |  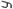 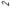 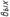 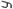 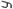  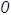 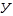 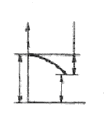
|
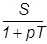
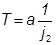
| 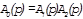 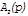 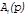 
| 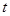  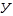 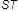 
|
При рассмотрении схемы 4, когда входная величина определяет движе-ние режущего инструмента к детали (например, врезное шлифование), а выходная контролирует деформацию в системе “деталь” и съем металла,
есть все основания ожидать проявления свойств инерционного звена наря-ду со свойствами деформирующего. И действительно, анализ системы под-тверждает это.
Моделирование САУ
Свойства любой системы проявляются в процессе ее функционирова-ния. Для определения этих свойств следует подать на входы некоторые возмущающие воздействия и проанализировать выходы системы. Однако почти всегда проведение таких экспериментов с реальной системой эконо-мически не выгодно. В связи с этим эксперименты для изучения свойств системы проводят не с реальными системами, а с их математическими мо-делями.
Модель – некоторая другая система, сохраняющая существенные черты оригинала и допускающая исследование физическими и математическими методами.
Моделирование – процесс проведения экспериментов на модели вместо прямых экспериментов на самой системе. В настоящее время широко при-меняют метод моделирования как способ научного познания реальной действительности, а в ряде случаев он оказывается единственным средст-вом познания сложных систем.
Чертеж детали, проект станка, система уравнений, описывающих техно-логический процесс управления последним, и другое – все это модели объ-екта проектирования, изготовления или управления.
Основой моделирования является теория подобия, которая утверждает, что абсолютное подобие моделируемого объекта или процесса и модели имеет место лишь при замене изучаемого объекта точно таким же. Модель должна отображать сущность исследуемого процесса, соответствовать це-ли конкретной задачи исследования, давать все необходимые данные для вычисления целевой функции и не содержать второстепенных связей. Мо-дель является абстракцией определенного варианта решения, дает возмож-ность многократного проведения опытов для познания сущности процесса и получения удовлетворительных результатов решения задачи. Изменяя характеристики системы, можно познать ее поведение при этих характе-ристиках и анализировать влияние различных факторов: наблюдать буду-
щие ситуации в виде, не искаженном посторонним влиянием, производить обобщение и оценивать новые идеи по совершенствованию организации исследуемого процесса. Поведение модели и реального объекта должно подчиняться одинаковым закономерностям. Изучив их на доступной для исследования модели, оказывается возможным предсказать свойства про-ектируемого объекта или процесса.
Многообразие исследуемых объектов и процессов, целей и задач моде-лирования породило множество типов моделей. Выбор аппарата для пост-роения модели зависит как от природы и свойств моделируемого объекта или процесса, так и от характера решаемой задачи. По способу построения все множество моделей можно разделить на физические и абстрактные.
Физическая (натуральная) модель – это установка или устройство, поз-воляющие проводить исследование заменой изучаемого физического про-цесса подобным ему процессом с сохранением его физической природы. Физические модели используются тогда, когда из-за сложности системы или недостаточной априорной информации не удается построить адекват-ную модель и когда даже с помощью моделирования на абстрактной мо-дели получение удовлетворительных результатов встречает непреодоли-мые трудности.
В процессе физического моделирования задают некоторые характерис-тики внешней среды и исследуют поведение либо реального объекта, либо его модели при заданных или задаваемых искусственно воздействиях внешней среды. Физическое моделирование может протекать в реальном или нереальном масштабе времени, а также может рассматриваться без учета времени.
Несмотря на универсальность метода физического моделирования пос-тановка натурального физического эксперимента с современными система-ми иногда бывает чрезвычайно затруднена, а порой и невозможна (напри-мер, причина и следствие разнесены во времени и пространстве). Избежать дорогостоящих натуральных экспериментов, сократить время на проверку гипотез позволяет использование абстрактных моделей.
В абстрактных моделях описание объектов и процессов осуществляется на каком-либо языке. В качестве языков моделирования можно использо-вать естественный язык, язык чертежей, схем, математический язык и др.
Описание объекта или процесса, выполненное на математическом язы-ке, называют математической моделью. В простейших случаях для этой цели используют известные аналоги между механическими, электрически-ми, и другими явлениями. Математические модели отличаются тем, что средством описания моделей и изучения их поведения является формаль-ный аппарат математики. Отсюда следует важное преимущество – широ-кая возможность количественного анализа моделей с помощью современ-ных математических методов. Другое важное преимущество математичес-ких моделей - универсальность языка математики, возможность исполь-зовать одни и те же модели для исследования физически различных систем.
Контрольные вопросы
1. Существует ли связь между вариантами соединения звеньев и устой-чивостью управления?
2. Какой параметр процесса резания может быть принят в качестве вы-ходной функции?
3. Характеризует ли передаточная функция динамические свойства сис-темы?
4. Какие задачи при исследовании систем можно решить с использова-нием годографов и ЛФЧХ?
5. Как преобразовать схему механической обработки в структурную схему системы управления?
Дата добавления: 2019-04-03; просмотров: 677;
