Структуры алгоритмов

Алгоритмы линейной структуры

Реализуют линейные вычислительные процессы, в которых отдельные этапы вычислений должны выполняться последовательно друг за другом. Линейные алгоритмы содержат только команды обработки данных. При исполнении алгоритма команды выполняются в порядке их записи. Линейный алгоритм вычисления коэффициентов приведенного квадратного уравнения рассмотрен в предыдущем разделе (рис. 9.2). Для построения таких алгоритмов используется структура следования.

Ветвления

Вычислительные процессы, в которых в зависимости от тех или иных условий должны выполняться различные этапы вычислений, называются разветвляющимися. Для построения алгоритмов, реализующих такие вычислительные процессы, необходимы специальные команды (управляющие структуры), позволяющие управлять ходом выполнения алгоритма, а менно, осуществлять выбор одного из нескольких возможных действий. Основной такой конструкцией является структура простого ветвления, реализующая принятие двоичного, или дихотомического, решения. Примером алгоритма с простыми ветвлениями является рассмотренный ранее алгоритм выбора максимального числа. Рассмотрим алгоритмы с более сложными ветвлениями.

Пример 9.5. Вычислить значение функции, график которой изображен на рис. 9.11.

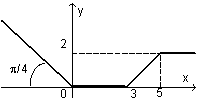
Рис. 9.11. График функции

Область определения функции разбивается на 4 участка, на каждом из которых значение функции определяется по различным формулам:

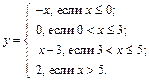
Для построения схемы алгоритма решения данной задачи используем вложенную конструкцию структур ветвления (рис. 9.12). Проверяем заданные условия последовательно. Первым проверим условие x £ 0 и, если оно выполняется, то вычислим y:= –x. Если первое условие не выполняется, то, следовательно, x > 0, и надо проверить следующее условие, x £ 3. Часть второго условия 0 < x можно не проверять, так как, если дело дошло до проверки этого условия, то заведомо 0 < x. Если условие x £ 3 выполняется, то вычислим y:= 0, иначе 3 < x, и проверяется условие x £ 5, проверка 3 < x исключается. Если действительно x £ 5, то вычисляем y:= x–3, а иначе 5 < x и вычисляем y:= 2, исключая проверку этого последнего условия. □

Рис. 9.12. Алгоритм вычисления значения функции
по заданному графику

Пример 9.6. Вычислить корни квадратного уравнения ax2 + bx + c = 0, a ¹ 0, в области действительных чисел. В зависимости от значения дискриминанта D = b² - 4ac возможны три случая:

1) квадратное уравнение не имеет действительных корней, если D < 0;

2) квадратное уравнение имеет два действительных равных корня, если D = 0: x₁ = x₂ = -b/2a;

3) квадратное уравнение имеет два действительных различных корня, если D > 0:

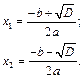
Схема алгоритма приведена на рис. 9.13. Алгоритм содержит сложное ветвление, являющееся композицией двух простых ветвлений.

Рис. 9.13. Алгоритм решения квадратного уравнения

К операндам вещественного типа не следует применять операцию отношения «=» (равно), условие может не выполняться из-за неточного представления вещественных чисел в памяти ЭВМ и неизбежных ошибок округления при вычислениях. В алгоритме отношение D = 0 заменено отношением |D| < e, где e – допустимая погрешность округления. □

Пример 9.7. Даны три числа а, b, с. Определить, имеется ли среди них хотя бы одна пара взаимно-обратных чисел.

Числа будут взаимно-обратными, если их произведение равно единице. В алгоритме производятся попарные проверки данных чисел. Если искомая пара найдена, выдается ответ «Да». Если же ни одна проверка не выявит пары взаимно-обратных чисел, выдается ответ «Нет». Алгоритм изображен на рис. 9.14, а. Этот алгоритм верно решает задачу, но не является структурным. Алгоритм легко преобразовать к структурному виду, если продублировать блок печати «Да» и вывести при этом найденные числа (рис. 9.14, б). Дублирование блоков – распространенный прием приведения алгоритмов с ветвлениями к структурному виду. Можно применить другой способ - введение сложных условий (рис. 9.14, в). □

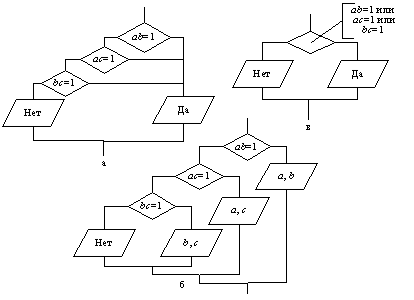
Рис. 9.14. Алгоритм поиска взаимно-обратных чисел

Циклы

Вычислительные процессы с многократным повторением однотипных вычислений/действий для различных значений входящих величин/данных называются циклическими, повторяемые участки вычислений – циклами, изменяющиеся в цикле величины – переменными цикла. Для организации циклов в алгоритмах необходимо предусмотреть (рис. 9.15):

- подготовку цикла – задание начальных значений переменным цикла перед первым его выполнением;

- тело цикла – вычислении/действия, повторяемые в цикле для различных значений переменных цикла;

- модификацию/изменение значений переменных цикла перед каждым новым его повторением;

- управление циклом – проверку условия продолжения/окончания цикла и переход на повторение цикла или его окончание.

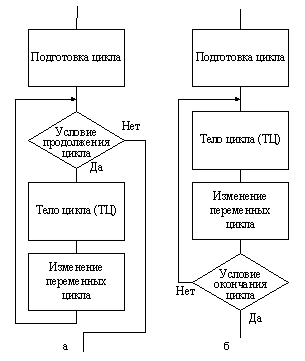
Рис. 9.15. Общие схемы циклического алгоритма

В зависимости от того, где осуществляется проверка условия продолжения или окончания цикла, последний относят к виду:

- цикла с предусловием, когда цикл начинается с проверки условия продолжения цикла (рис. 9.15, а);

- цикла с постусловием, когда условие проверяется после выполнения тела цикла (рис. 9.15, б).

Наиболее наглядным примером циклического вычислительного процесса является задача табулирования функции: вычисления значений функции y = f(x) для значений аргумента x, изменяющихся от начального x₀ до конечного x_n с постоянным шагом h_x (рис. 9.16). Здесь многократно повторяемые действия (тело цикла) – это вычисление значения функции f(x) для очередного значения аргумента x и вывод полученного результата на печать; переменная цикла – переменная x. Цикл выполняется для значений x, равных x₀, x₀ + h_x, x₀ + 2h_x, ..., x_n. Для модификации переменной x в цикле её значение надо увеличивать на значение шага: x := x + h_x. Для управления циклом можно использовать структуру цикла как с предусловием, где x <= x_n – условие продолжения цикла (рис. 9.16, а), так и с постусловием, где x > x_n – условие окончания цикла (рис. 9.16, б).

Рис. 9.16. Общие схемы алгоритма табулирования функции

Алгоритмы табулирования функции с пред- и постусловием дают, вообще говоря, одинаковый результат. Но тело цикла с предусловием в определенной ситуации может не выполниться ни разу, а тело цикла с постусловием обязательно выполняется хотя бы один раз.

Рассмотрим случай, когда нижняя граница x₀ переменной x превышает верхнюю x_n. В этой ситуации цикл не должен выполняться ни разу. Поэтому в задаче табулирования функции лучше использовать цикл с предусловием, цикл же с постусловием может дать неверный результат. Приведем пример целесообразного использования цикла с постусловием.

Пример 9.8. Составим алгоритм вычисления суммы всех целых чисел, вводимых с терминала до тех пор, пока не будет введен нуль.

Накопление суммы S будем осуществлять в цикле путем прибавления очередного введенного числа k к сумме всех предыдущих: S := S + k. Перед началом цикла значение переменной S обнулим: S := 0. Проверка условия окончания цикла возможна лишь после ввода хотя бы одного числа, поэтому лучше использовать цикл с постусловием. Алгоритм вычисления искомой суммы представлен на рис. 9.17. □

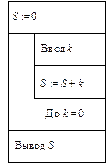
Рис. 9.17. Алгоритм вычисления суммы вводимых чисел

Помимо циклов с пред- и постусловием принято различать циклы с заранее неизвестным и известным числом повторений. Примером цикла первого типа могут служить алгоритм вычисления суммы (пример 9.8) и алгоритм Евклида. Примером цикла второго типа – алгоритм табулирования функции, где число повторений цикла N_x определяется как

N_x = [(x_n – x₀)/h_x] + 1,

где квадратные скобки [ ] означают целую часть числа.

В циклах с известным числом повторений всегда можно выделить переменную, определяющую число повторений цикла, значение которой изменяется по заданному закону, например, от начального до конечного с постоянным шагом. Такая переменная используется для управления циклом: в условии окончания цикла осуществляется сравнение текущего значения переменной с заданным порогом. Эту переменную именуют параметром цикла, а сам цикл - циклом с параметром.

Для схемного представления цикла с параметром используют специальную управ ляющую структуру с блоком модификации (рис. 9.18), где указывают закон изменения параметра цикла. Например, в задаче табулирования функции y = f(x) параметром цикла является переменная x, закон изменения которой можно представить в виде x = x₀ (h_x) x_n.

Схема цикла с параметром для табулирования функции одной переменной приведена на рис. 9.18. На схеме вход 1 в блок i – первоначальный вход в цикл, вход 2 – очередное повторение цикла, выход 3 – окончание цикла.

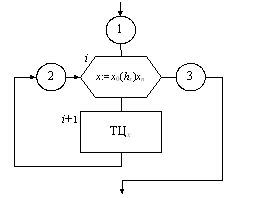
Рис. 9.18. Схема цикла с параметром

Блок модификации включает в себя подготовку цикла (x := x₀), изменение параметра цикла при его очередном повторении (x := x + h_x), управление циклом – проверку условия его продолжения (x < x_n) и переход на продолжение или окончание цикла. При этом явно выделено тело цикла. Проверка условия x < x_n проводится перед каждым, в том числе первым, выполнением цикла, как в цикле с предусловием. И если начальное значение параметра цикла больше конечного, то цикл не выполняется ни разу.

Для записи цикла с параметром в языках программирования существует специальный оператор – оператор цикла с параметром.

Пример 9.9. Составим алгоритм табулирования сложной функции, приведенный на рис. 9.10, используя структуру цикла с параметром. Алгоритм представлен на рис. 9.19. Тело цикла в этом алгоритме представляет собой композицию двух вложенных структур ветвления и структуры следования.

В схеме алгоритма в качестве параметра цикла может выступать переменная любого типа. При реализации этой структуры в различных языках программирования синтаксис оператора цикла с параметром может не допускать использование параметра цикла вещественного типа, как, например, в языке Паскаль. Тогда необходимо введение дополнительной переменной целого типа, определяющей количество значений x, y и используемой в качестве параметра цикла. □

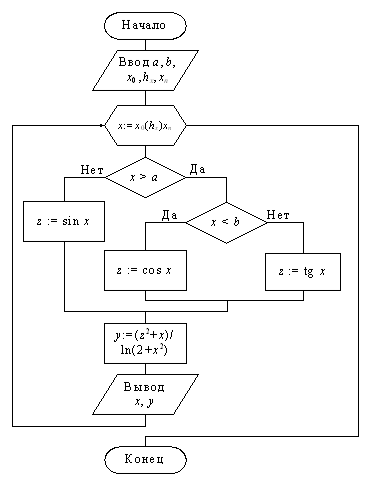
Рис. 9.19. Алгоритм табулирования сложной функции

Пример 9.10. Вычислить степень Y = aⁿ действительного числа a с натуральным показателем n. Воспользоваться для вычислений следующей формулой: aⁿ = a × a × …× a – n раз.

Компактно произведение может быть записано в виде

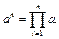
Для вычисления Y организуем цикл с параметром i, в котором будем накапливать искомое произведение по следующему правилу: до начала цикла положим Y = 1, а в цикле будем домножать n раз накопленное ранее произведение на a, т. е. Y := Y·a. Алгоритм представлен на рис. 9.20. □

Пример 9.11. Вычислим сумму квадратов всех целых чисел из заданного интервала [m, n]. В компактной форме записи:

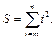
Для вычисления указанной суммы организуем цикл с параметром, в котором будем n раз вычислять значение очередного слагаемого y := i² и накапливать искомую сумму S := S + y. До начала цикла положим S := 0. Алгоритм приведен на рис. 9.21. □

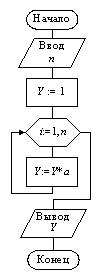Рис. 9.20. Алгоритм вычисления конечного произведения

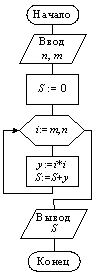Рис. 9.21. Алгоритм вычисления конечной суммы

Пример 9.12. Определим, какое количество точек (x, y) из заданного множества x = x₀ + ih_x; y = y₀ + ih_y; i = 0, 1, ..., 20, находится в каждой из заштрихованных областей D1 и D2, включая их границы (рис. 9.22).

Пример иллюстрирует цикл с несколькими переменными цикла. Число анализируемых точек определяется количеством значений переменной i. Организуем цикл с параметром i, в котором будем изменять значения переменных x, y и для каждой очередной пары (x, y) проверять условия её принадлежности к одной из заданных областей.

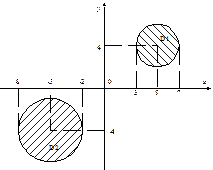
Рис. 9.22. Области определения

Условие попадания точки (x, y) в область D1 – окружность радиусом 2 с центром в точке (5, 4): (x - 5)² + (y - 4)² £ 4.

Условие попадания точки (x, y) в область D2 – окружность радиусом 3 с центром в точке (-5, -4): (x + 5)² + (y + 4)² £ 9.

Для проверки условий и подсчета количества KolD1, KolD2 точек, попавших в каждую из областей, используем структуры сокращенного ветвления. Перед циклом надо задать переменным их начальные значения (рис. 9.23). □

Итерационные циклы

Среди циклов с неизвестным числом повторений большое место занимают циклы, в которых в процессе повторения тела цикла образуется последовательность значений a₁, a₂, ..., a_n, ..., сходящаяся к некоторому пределу a:

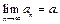
Каждое новое значение a_n в такой последовательности является более точным приближением к искомому результату a. Циклы, реализующие такую последовательность приближений/итераций, называют итерационными.

В итерационных циклах условие окончания цикла основывается на свойстве безграничного приближения значений a_n к искомому пределу с увеличением n. Итерационный цикл заканчивают, если для некоторого значения n выполняется условие

|a_n – a_n–1| £ e,

где e – допустимая погрешность вычислений. При этом результат отождествляют со значением a_n, т. е. считают, что a_n = a.

Рис. 9.23. Алгоритм подсчета числа точек,
принадлежащих заданным областям

Пример 9.13. Составим алгоритм вычисления с заданной погрешностью e, используя следующее рекуррентное соотношение:

y_n = y_n-1 - (x/y_n-1 - y_n-1)/2; y₁ = x/2.

Условием окончания данного итерационного цикла будет условие |y_n – y_n–1| £ e. Для его проверки необходимо иметь два приближения: текущее y_n и предыдущее y_n-1. Алгоритм можно упростить, если ввести вспомогательную переменную d = y_n - y_n-1 = (x/y_n-1 - y_n-1)/2 и использовать ее в условии окончания цикла: | d | £ e. Для проверки такого условия достаточно иметь лишь одно приближение, которое обозначим через y.

Алгоритм вычисления квадратного корня представлен на рис. 9.23. Для организации итерационного процесса использована структура цикла с постусловием. □

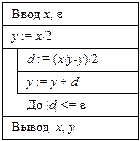
Рис. 9.23. Алгоритм вычисления квадратного корня

Вложенные циклы

В практике алгоритмизации достаточно часто встречаются задачи, при решении которых необходимо проектировать алгоритмы с несколькими циклами. Если в теле цикла содержится один или несколько других циклов, то такие циклы называют вложенными. Цикл, содержащий в себе другой цикл, называют внешним. Цикл, содержащийся в теле другого цикла, называют внутренним.

Выполняются вложенные циклы следующим образом. Сначала при фиксированных начальных значениях переменных внешнего цикла полностью выполнится внутренний цикл и его переменные «пробегут» все свои значения. Затем переменные внешнего цикла примут следующие значения и, если условие окончания внешнего цикла не будет достигнуто, снова полностью выполнится внутренний цикл и его переменные опять «пробегут» все свои значения и т. д. до тех пор, пока не выполнится условие окончания внешнего цикла.

Пример 9.14. Составим алгоритм табулирования сложной функции двух переменных:

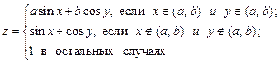
для x = x₀(h_x) x_n и y = y₀(h_y) y_n.

Вычисление значений функции z для всех различных пар (x, y) необходимо организовать следующим образом. Вначале при фиксированном значении одного из аргументов, например, при x = x₀, вычислить значения z для всех заданных y: y₀, y₀ + h_y, y₀ + 2h_y, ..., y_n. Затем, изменив значение x на x₀ + h_x, вновь перейти к полному циклу изменения переменной y. Данные действия повторить для всех x: x₀, x₀ + h_x, x₀ + 2h_x, ..., x_n.

Для записи алгоритма необходима структура вложенных циклов, например, с параметром: внешнего – с параметром x и внутреннего – с параметром y. В данной задаче внешний и внутренний циклы можно поменять местами, при этом изменится только порядок изменения аргументов.

Общее количество значений z равно N_z = N_xּN_y, где

N_x = [(x_n – x₀)/h_x] + 1, N_y = [(y_n – y₀)/h_y] + 1.

Алгоритм табулирования функции, выполненный по технологии нисходящего проектирования, представлен на рис. 9.25.

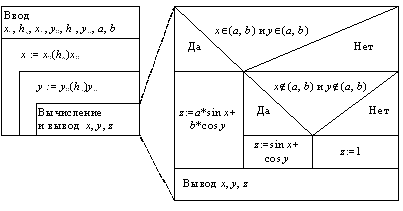
Рис. 9.25. Алгоритм табулирования функции двух переменных

На первом этапе составлена укрупненная схема решения задачи с выделением операции ввода исходных данных и структуры вложенных циклов. На втором этапе раскрывается тело внутреннего цикла как композиция структур ветвления. □

Пример 9.15. Найти совершенное число в интервале [2, n]. Совершенное число равно сумме всех своих делителей, включая единицу. Например, 28 – совершенное число, так как 28 = 1 + 2 + 4 + 7 + 14.

В алгоритме для каждого целого k из заданного интервала будем определять сумму S всех его делителей и сравнивать значения S и k. Если они равны, то анализируемое k есть искомое совершенное число, надо его вывести и закончить поиск, в противном случае, перейти к следующему целому числу из заданного интервала.

Для реализации такого алгоритма необходима структура вложенных циклов: внешнего, для просмотра заданного интервала, и внутреннего, для вычисления суммы (рис. 9.26, а). Построенный алгоритм не является структурированным. Рассмотрим один из способов приведения циклического алгоритма к структурному виду. Внешний цикл имеет два условия окончания: исчерпание всех целых чисел из заданного интервала и выполнение равенства k = S. В зависимости от того, какое условие привело к окончанию цикла, необходимо предпринять различные действия. Объединим оба условия окончания цикла в одно: k > n или k = S. Для принятия окончательного решения после завершения цикла проверим, какое же условие привело к его окончанию (рис. 9.26, б).

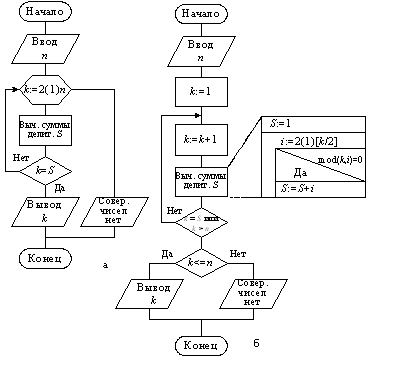
Рис. 9.26. Алгоритм поиска совершенного числа

Можно структурировать алгоритм иначе: в цикле с параметром k ввести дополнительную переменную Pr, установив до цикла Pr = 0. Как только совершенное число будет найдено, присвоить Pr значение этого числа. Окончательное решение в этом случае принимается уже на основании анализа признака Pr.

Структура внутреннего цикла для вычисления суммы S раскрывается на втором этапе детализации алгоритма. Поскольку все числа делятся на единицу, то сначала устанавливается S = 1. В цикле с параметром i, изменяющимся от 2 до [k/2], суммируются все делители числа k. В интервале от [k/2]+1 до k–1 не может быть делителей числа k. □