Технология разработки алгоритмов

Опыт практической алгоритмизации и программирования привел к формированию неких общих принципов и методов проектирования, разработки и оформления алгоритмов.

Какими качествами должен обладать хороший алгоритм?

Прежде всего, от алгоритма требуется, чтобы он правильно решал поставленную задачу. Но не менее важно, какой ценой это достигается. Речь идет о разумности затрат на его создание. С этой точки зрения алгоритм должен быть легким для понимания, простым для доказательства правильности и удобным для модификации. В рамках такой идеологии и сформировался так называемый структурный подход к конструированию и оформлению алгоритмов, позволяющий уменьшить количество ошибок в алгоритмах, упрощающий их контроль и модификацию.

По своей сути структурный подход есть отказ от беспорядочного стиля в алгоритмизации и программировании (в частности, отказ от оператора go to) и определение ограниченного числа стандартных приемов построения легко читаемых алгоритмов и программ с ясно выраженной структурой. Теоретическим фундаментом этого подхода является теорема о структурировании, из которой следует, что алгоритм решения любой практически вычислимой задачи может быть представлен с использованием трех элементарных базисных управляющих структур: а) структуры следования или последовательности; б) структуры ветвления; в) структуры цикла с предусловием (рис. 9.7, соответственно а, б, в, где P – условие, S – оператор).

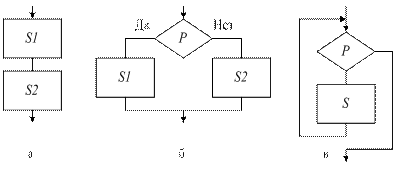
Рис. 9.7. Базисные управляющие структуры

Базисный набор управляющих структур является функционально полным, то есть с его помощью можно создать любой сколь угодно сложный алгоритм. Однако с целью создания более компактных и наглядных алгоритмов дополнительно используются следующие управляющие структуры: а) структура сокращенного ветвления; б) структура выбора; в) структура цикла с параметром; г) структура цикла с постусловием (рис. 9.8, соответственно а, б, в, г).

В разных языках программирования реализация базовых управляющих структур может быть различной. В языке Паскаль реализованы все рассмотренные структуры.

Рис. 9.8. Дополнительные управляющие структуры

Любой алгоритм может быть построен посредством композиции базисных и дополнительных структур:

- путем их последовательного соединения - образования последовательных конструкций;

- путем их вложения друг в друга - образования вложенных конструкций.

Например, алгоритм Евклида, описанный ранее, представляет собой комбинацию из трех управляющих структур: последовательности, цикла и ветвления (рис. 9.9).

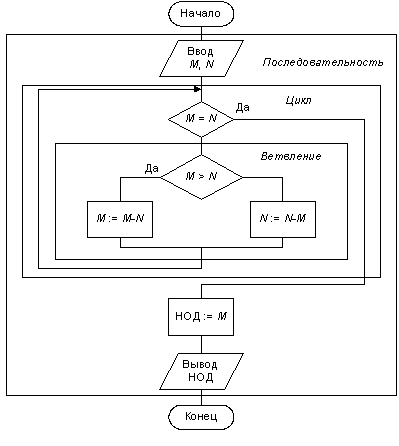
Рис. 9.9. Алгоритм Евклида как композиция базисных структур

Каждая из структур может рассматриваться как один блок с одним входом и одним выходом. Таким образом, мы можем ввести преобразование любой структуры в функциональный блок. Тогда всякий алгоритм, составленный из стандартных структур, поддается последовательному преобразованию к единственному функциональному блоку и эта последовательность преобразований может быть использована как средство понимания алгоритма и доказательства его правильности. Обратная последовательность преобразований может быть использована в процессе проектирования алгоритма по нисходящей схеме с постепенным раскрытием единственного функционального блока в сложную структуру основных элементов. В области автоматизированной обработки данных такой подход называют нисходящим проектированием или проектированием «сверху вниз».

Разработка алгоритма по нисходящей схеме начинается с разбиения сложной исходной задачи на отдельные более простые подзадачи, решение которых может быть представлено в общей структуре алгоритма функционально независимыми блоками. Разработку логической структуры каждого такого блока и ее модификацию можно осуществлять независимо от остальных блоков. На первом этапе проекта раскрываются наиболее важные и существенные связи в исследуемой задаче, составляется укрупненная схема алгоритма, определяется функциональное назначение каждого блока, его входные и выходные данные. На последующих этапах проектирования уточняется логическая структура отдельных функциональных блоков общей схемы, строятся схемы алгоритмов выделенных ранее подзадач. Разработка алгоритма каждой подзадачи также может осуществляться в несколько этапов детализации. На каждом этапе проекта выполняются многократные проверки и исправления алгоритма. Подобный подход является достаточно рациональным, позволяет значительно ускорить процесс разработки сложных алгоритмов, и в значительной мере избежать ошибочных решений.

В качестве примера рассмотрим задачу табулирования функции одной переменной, то есть вычисление значений функции у = f(x) для всех значений х, изменяющихся от х₀ до х_n с шагом h_x, сокращенно:
x = х₀(h_x) х_n.

Пусть

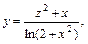где

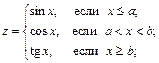
a, b, x₀, h_x, x_n – исходные данные.

Процесс проектирования алгоритма табулирования функции у = f(x) показан на рис. 9.10, а. На первом уровне детализации схема отражает процесс табулирования функции в общем виде (блоки 1.1-1.5). Далее осуществляется детализация блока 1.4 в виде последовательности блоков 2.1-2.3 второго уровня. Функция z = z(x), входящая в определение исходной функции, представлена разветвляющейся структурой третьего уровня детализации (блоки 3.1-3.5).

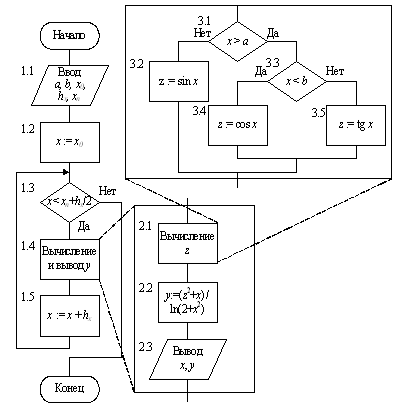
а

Рис. 9.10. Нисходящая схема проектирования
алгоритма вычисления сложной функции

Подставляя вместо функциональных блоков, подвергнутых дальнейшей детализации, соответствующие структуры, получим окончательную схему алгоритма, изображенную на рис. 9.10, б.

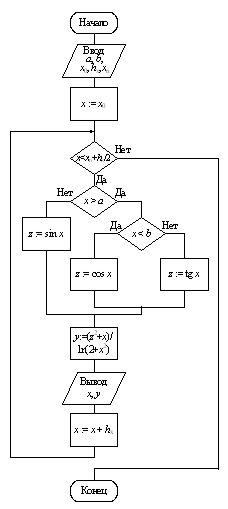
б

Рис. 9.10. Окончание. Алгоритм вычисления сложной функции