Проверка гипотезы о виде закона распределения. Критерии согласия

Во многих практических задачах модель закона распределения заранее неизвестна, поэтом возникает вопрос выбора модели, согласующейся с результатами наблюдения надс.в.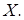

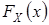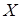Предположим, что неизвестная функция распределения с.в. имеет определенную модель 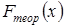, то есть сформулируем гипотезу 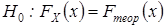. Тогда в качестве альтернативной выдвинем гипотезу 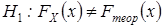. Требуется сделать вывод: согласуются ли данные наблюдений с высказанным предположением?

Определение 24.Критерием согласия называется критерий, с помощью которого проверяется гипотеза о предполагаемом виде закона распределения (о согласовании предполагаемого вида распределения с опытными данными на основании выборки).

Критерий Пирсона

Для проверки гипотезы 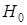поступим следующим образом. Разобъем всю область значений с.в. 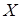на 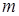интервалов 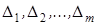и подсчитаем вероятности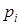 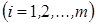попадания с.в. 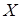в интервал 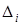по формуле

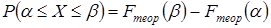
(26)

Тогда теоретическое число значений с.в. X, попавших в интервал 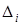, можно вычислить по формуле

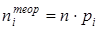
(27)

Таким образом, получим вариационный ряд распределения и теоретический ряд распределения. Если эмпирические частоты сильно отличаются от теоретических, то проверяемую гипотезу 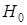отвергаем, в противном случае – принимаем ее.

В качестве критерия, характеризующего степень расхождения между эмпирическими и теоретическими частотами, К.Пирсон предложил статистику

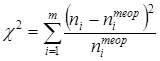
(28)

При 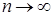эта величина имеет 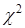– распределение с 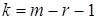степенями свободы, где 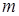– число интервалов выборки, 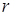– число параметров предполагаемого распределения. Например, в случае нормального распределения оценивают два параметра 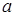и 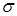, поэтому .

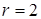Схема применения критерия 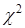Пирсона сводится к следующему:

1. По формуле (41) вычисляем 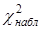– выборочное значение статистики критерия.

2. Задав уровень значимости 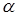критерия, по таблице 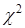– распределения находим критическую точку (квантиль) .

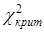3. Если 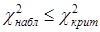, то гипотеза 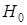не противоречит данным наблюдений; в противном случае если 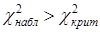, гипотезу 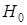отвергаем.

Необходимым условием применения критерия 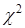Пирсона является выполнение соотношения 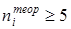. Если для какой-то группы выборки оно не выполняется, такую группу объединяют с соседней и соответственно уменьшают число групп.