Сложение двоичных чисел с плавающей запятой

При выполнении операции сложения двоичных чисел с плавающей запятой необходимо иметь в виду, что сложение возможно только в том случае, когда порядки слагаемых одинаковы. Поэтому операция сложения включает два этапа: этап выравнивания порядков, т.е. приведения обоих слагаемых к большему из порядков, и собственно сложения мантисс. Для обработки порядков и мантисс используются разные группы аппаратных средств, т.е. в схеме операционного автомата (ОА) используются две группы элементов: одна из них предназначена для обработки порядков, другая – для обработки мантисс.

При выполнении любых арифметических операций порядки всегда обрабатываются в модифицированных кодах. Это необходимо для контроля переполнения разрядной сетки порядка. Мантиссы при выполнении сложения с плавающей запятой также обрабатываются в модифицированных кодах, что позволяет использовать критерии нормализованности результата сложения.

Для сложения двух чисел с одинаковыми значениями порядка достаточно сложить мантиссы двух операндов и присвоить порядку результата значение порядка одного из слагаемых. Если порядки слагаемых имеют разные значения, то вначале необходимо произвести выравнивание порядков. Для выравнивания порядков необходимо привести оба слагаемых к большему из порядков путем сдвига мантиссы меньшего числа вправо на такое число разрядов, на какое различаются порядки слагаемых. При этом следует формализовать процедуру нахождения меньшего из двух чисел, представленных в форме с ПТ, и сформулировать критерий, позволяющий выполнить необходимые преобразования мантиссы меньшего числа. После выравнивания порядков мантиссы можно складывать обычным образом. Порядку результата присваивается значение большего из порядков слагаемых. Следует позаботиться о том, чтобы больший из порядков был сохранен для упомянутого присваивания. Процедура выравнивания порядков выполняется всегда перед началом сложения.

Допустим, что необходимо сложить два двоичных числа, представленных в форме с ПТ: mA*2^ПА+mB*2^ПВ=mC*2^ПС.

Опишем последовательность действий, выполняемых при сложении с ПТ.

1. Выравнивание порядков. Определяется значение разности порядков слагаемых: 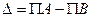. Дальнейшие действия зависят от значения D следующим образом:

a. Если D>0, это означает, что порядок А больше, чем порядок В, и следовательно, порядку результата надо присвоить значение ПА, а мантиссу числа В - сдвинуть на D разрядов вправо. Для этого необходимо, выполнив сдвиг mB на один разряд вправо, вычесть 1 из разности D. Если полученная разность не окажется равной 0, продолжить сдвиги мантиссы В, пока D не станет равной 0.

b. Если D<0, это означает, что порядок числа В больше порядка числа А. В этом случае порядку результата присваивается значение порядка числа В (ПВ), и выполняются сдвиги вправо мантиссы числа А с одновременным увеличением D на 1 на каждом сдвиге, до тех пор пока не будет выполнено условие D=0.

c. Если D=0, это означает, что порядки операндов равны, порядку результата присваивается значение порядка одного из слагаемых (любого).

2. Сложение мантисс. Очевидно, что процедура выравнивания порядков заканчивается, когда D=0. После этого выполняется сложение мантисс, представленных в модифицированном коде. В результате выравнивания порядков одна из мантисс может оказаться не нормализованной. Формат мантиссы результата имеет вид: Sg1Sg2, c₁c₂…c_n, где n –количество числовых разрядов мантиссы Прежде чем отправлять полученный результат в память ЭВМ, необходимо произвести его нормализацию

3. Нормализация результата. Необходимость в нормализации возникает в том случае, когда мантисс результата не удовлетворяет условию нормализации: 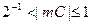. Критерием нарушения нормализации справа (переполнения разрядной сетки) является признак d: 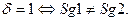Если в результате сложения мантисс образовалось переполнение разрядной сетки, т.е. нарушение нормализации справа, необходимо выполнить следующие действия: сдвинуть мантиссу результата арифметическим сдвигом на один разряд вправо, и для сохранения правильного значения результата увеличить порядок на единицу.

Критерием нарушения нормализации слева является признак l: 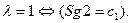Нарушение нормализации слева может возникнуть при сложении чиселс разными знаками. Если складываются числа близкие по абсолютной величине и с разными знаками, то результат сложения может оказаться <2^-1 или нулевым. В этом случае нормализация состоит в том, что мантиссу результата сдвигают арифметическим сдвигом влево до тех пор, пока l=1, вычитая 1 из порядка результата при каждом сдвиге мантиссы влево. Если в результате сложения получена нулевая мантисса, то ее не нормализуют, и порядок обнуляют. Такой результат не является ошибкой, так как это число может участвовать в операции сложения. Для обнаружения нулевого результата на выходе сумматора мантисс используют компаратор, выходной сигнал которого равен 1 тогда и только тогда, когда мантисса суммы равна нулю. Если такая комбинационная схема не используется для проверки значения результата, необходимо поставить ограничитель на число сдвигов мантиссы суммы влево, например, с помощью счетчика. В этом случае счетчику присваивают значение n-1 и выполняют декремент счетчика при каждом сдвиге мантиссы суммы влево. Если после выполнения всех сдвигов признак нарушения нормализации слева продолжает оставаться равным 1, это является критерием нулевого результата. Однако этот способ требует больших затрат времени по сравнению с использованием компаратора.

4. После завершения нормализации результата необходимо проверить, нет ли переполнения разрядной сетки порядка в результате выполнении нормализации результата. Критерием переполнения разрядной сетки порядка является различное начертание первого и второго знаковых разрядов: 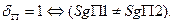Если при наличии переполнения SgП1=1, говорят об отрицательном переполнении разрядной сетки. В этом результату сложения присваивается машинный нуль, т. е. мантисса и порядок результата обнуляются. Если при наличии переполнения разрядной сетки порядка SgП1=0, это говорит о том, что результат не может быть представлен в данной разрядной сетке и вырабатывается требование прерывания. Если переполнение разрядной сетки отсутствует, то в регистр результата засылаются порядок и мантисса результата, которые по шине данных отправляются в память.

Пример.

Выполнить сложение двух чисел А= 274₁₀, В=-39₁₀, на Двоичном сумматоре дополнительного кода. Результат представить в нормализованной форме.

Вначале выполним перевод слагаемых в форму с плавающей запятой.

274₁₀=100010010₂=0,100010010*2⁹;

39₁₀=100111₂=0,100111*2^6.

Далее необходимо выбрать параметры функциональных элементов операционного автомата, т.е. длину разрядной сетки регистров, в которых будут храниться исходные и промежуточные данные и результаты счета.

Примем следующие параметры данных во внешней памяти: разрядность порядка n_П=4+1, т.е. 4 числовых разряда и один знаковый разряд; разрядность мантиссы n_M=6+1, т.е. 6числовых разрядов и один знаковый разряд.. Для размещения исходных данных в регистровой памяти операционного автомата потребуется 4+1+6+1=12 разрядов. Допустим, что в схеме ОА имеется два 12-разрядных регистра, в один из которых (РгА) помещают первое слагаемое, и в другой (РгВ) – второе слагаемое. Слагаемые находятся во внешней памяти в дополнительном коде.

Для обработки порядков будем использовать 6-разрядные регистры РгПА и РгПВ, в которые будут загружены порядки операндов из РгА и РгВ в модифицированных кодах, а также 6-разрядный сумматор дополнительного кода СмП. Формат микроопераций загрузки имеет вид:

РгПА:=РгА[0]|РгА[0-4], РгПB:=РгB[0]|РгB[0-4].

В группу аппаратных средств, предназначенных для обработки порядков необходимо также включить комбинационную схему компаратора, для получения информации о моменте, когда на выходе СмП образуется нуль. Последнее является свидетельством окончания процедуры выравнивания порядков.

В группу аппаратных средств, предназначенных для обработки мантисс включим два 8-разрядных регистра мантисс со сдвигом вправо, РгМА и РгМВ, в которые загружаются мантиссы слагаемых из РгА и РгВ соответственно, а также сумматор такого же формата. Формат соответствующих микроопераций имеет вид:

РгМА:=РгА[5]|РгА[5-11], РгМВ:= РгВ[5]|РгВ[5-11].

Перед началом работы сумматоры «обнуляются». Последовательность действий, выполняемых при сложении представлена в Табл. 5.

Таблица 5 Пример сложения двоичных чисел с плавающей запятой

СмП	РгМА	РгМВ	СмМ	Примечания
00.0000 +00.1001 00.1001	00.100010	11.011001	00.000000	СмП:=0, СмМ:=0, РгМА:=[MA]дм, РгМВ:=[MB]дм, РгПА:=[ПA]дм, РгПВ:=[ПB]дм
			СмП:=СмП+РгПА,
+11.1010				СмП:=СмП+ ,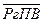
00.0011 +11.1111 00.0010 +11.1111 00.0001 +11.1111 00.0000		11.101100   11.110110   11.111011		СмП=0? НЕТ Начинаем процедуру выравнивания порядков. Sg1СмП=1, следовательно А>B. Порядку результата присваиваем значение ПА. Будем увеличивать содержимое СмП на 1и сдвигать одновременно РгМА вправо на один разряд, пока СмП¹0.
			00.000000 +00.100010 00.100010 +11.111011 00.011101	СмП=0? ДА Следовательно, порядки выровнены. Начинаем сложение мантисс. СмМ:=СмМ+РгМА,
			СмМ:=СмМ+РгМВ,
00.0000 +00.1001 00.1001 +11.1111 00.1000			00.111010	СмМ[0]=СмМ[2]. Следовательно, нет переполнения разрядной сетки мантиссы. СмМ[0]=СмМ[3], следовательно, имеет место нарушение нормализации слева. Для нормализации результата выполним сдвиг мантиссы результата вправо на 1 разряд влево: СмМ:=L(1)СмМ и вычтем 1 из порядка результата, который предварительно поместим в СмП, выполнив микрооперацию СмП:=РгПА.
				СмМ[0]=СмМ[3]? НЕТ Следовательно, нормализация результата закончена. Проверка СмП на переполнение разрядной сетки: СмП[0]=СмП[1]? ДА, Переполнение разрядной сетки отсутствует. Сложение закончено. Результат помещаем в РгА: РгА:=СмП[1-5]|СмМ[1-7],
				Завершение операции – передача результата во внешнюю память по шине данных: ШД:=РгА

Результат сложения С=0.111010*2⁸=232. Ошибка сложения (274-39=235) обусловлена недостаточной длиной разрядной сетки, а также потерей значащих разрядов при выполнении выравнивания порядков.