Определение точности измерений

3.4.1 Понятие погрешности измерения

При практическом использовании тех или иных результатов измерений важно оценить их точность. Термин «точность измерений», т. е. степень приближения результатов измерения к некоторому истинному значению, не имеет строгого определения и используется для качественного сравнения измерительных операций. Для количественной оценки применяется понятие «погрешность измерений» (чем меньше погрешность, тем выше точность).

Погрешностью называют отклонение результата измерений от истинного (действительного) значения измеряемой величи­ны. При этом следует иметь в виду, что истинное значение физической величины считается неизвестным и применяется в теоретических исследованиях. Действительное значение физической величины устанавливается экспериментальным путем в предположении, что результат эксперимента (измерения) в максимальной степени приближается к истинному значению. Оценка погрешности измерения - одно из важных мероприятий по обеспечению единства измерений.

Погрешность измерений зависит в первую очередь от погрешностей СИ, а также от условий, в которых проводится измерение, от экспериментальной ошибки методики и субъективных особенностей человека в случаях, где он непосредственно участвует в измерениях. Поэтому можно говорить о нескольких составляющих погрешности измерений или о ее суммарной погрешности.

Количество факторов, влияющих на точность измерения, достаточно велико, и любая классификация погрешностей измерения (рисунок.15) в известной мере условна, так как различные погрешности в зависимости от условий измерительного процесса проявляются в разных группах.

Рисунок 15 – Классификация погрешностей измерения

3.4.2 Виды погрешностей

Как указывалось выше, погрешность измерения – это отклонение результата измерения Х от истинного Х_и значения измеряемой величины. При этом вместо истинного значения физической величины Х_и используют ее действительное значение Х_д.

В зависимости от формы выражения различают абсолютную, относительную и приведенную погрешности измерения.

Абсолютная погрешность – это погрешность средства измерений, выраженная в единицах измеряемой физической величины. Она определяется как разность Δ'= Х_i - Х_и или Δ = X - Х_д., где X_i – результат измерения.

Относительная погрешность – это погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерений к результату измерений или действительному значению измеряемой физической величины. Она определяется как отношение δ = ±(Δ/Х_д)·100%.

Приведенная погрешность – выраженное в % отношении измеряемой величины к значению абсолютной погрешности прибора, которое соответствует конечной отметке шкалы этого прибора, называют относительной приведенной погрешностью прибора.

γ=±(Δ/Χ_n)·100%

В качестве нормирующего значения (Χ_N) используют диапазон измерений прибора. Главная предельно допустимая приведенная погрешность прибора обуславливает класс точности этого прибора. Классы точности: 0,05; 0,1; 0,2;1,0; 1,5; 2,5; 4,0.Так, приборы класса точности 2,5 имеют допустимую приведенную погрешность 2,5%. Сведения о погрешности прибора, как правило, указывают на его шкале, а также в паспорте прибора. Они позволяют осуществить подходящий правильный подбор в зависимости от условий эксплуатации и определённо помогают правильно использовать прибор при выполнении измерений.

Методами теории вероятностей установлено, что в качестве действительного значения результата при многократных измерениях параметра, изменяющегося случайным образом, выступает среднее арифметическое значение X:

X = 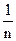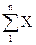_i ,

где X_i – результат i -го измерения, n – число измерений.

Величина `X, полученная в одной серии измерений, является случайным приближением к Х_и. Для оценки ее возможных отклонений от Х_и определяют оценку среднего квадратического отклонения от среднего арифметического:

S(`X)=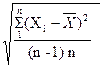

Для оценки рассеяния отдельных результатов измерения Xi относительно среднего арифметического `X определяют выборочное среднее квадратическое отклонение:

σ =

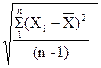
Эти формулы соответствуют центральной предельной теореме теории вероятностей, согласно которой среднее арифметическое из ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого определенного измерения:

S(`X)= σ /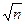

Эта формула отражает фундаментальный закон теории погрешностей. Из него следует, что если необходимо повысить точность результата (при исключенной систематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если точность требуется увеличить в 3 раза, то число измерений увеличивают в 9 раз и т.д.

Нужно четко разграничивать применение величин S и σ: первая используется при оценке погрешностей окончательного результата, а вторая – при оценке погрешности метода измерения.

В зависимости от характера проявления, причин возникновения и возможностей устранения различают систематическую и случайную погрешности измерений, а также грубые погрешности (промахи).

Систематическая погрешность – это составляющая погрешности, принимаемая за постоянную или закономерно изменяющуюся при повторных измерениях одного и того же параметра. Как правило, считают, что систематические погрешности могут быть обнаружены и исключены. Однако в реальных условиях полностью исключить эти погрешности невозможно. Всегда остаются какие-то неисключенные остатки, которые нужно учитывать, чтобы оценить их границы. Это и будет систематическая погрешность измерения.

Случайная погрешность – это составляющая погрешности, изменяющаяся в тех же условиях измерения случайным образом. Значение случайной погрешности заранее неизвестно, она возникает из-за множества не уточненных факторов. Исключить из результатов случайные погрешности нельзя, но их влияние может быть уменьшено путем статистической обработки результатов измерений.

Случайная и систематическая составляющие погрешности из­мерения проявляются одновременно, так что при их независимости их общая погрешность равна сумме погрешностей. В принципе систематическая погрешность тоже случайна и указанное деление обусловлено лишь установившимися традициями обработки и представления результатов измерения.

В отличие от случайной погрешности, выявляемой в целом, вне зависимости от ее источников, систематическая погрешность рассматривается по составляющим в зависимости от источников ее возникновения. Различают субъективную, методическую и инструментальную составляющие систематической погрешности.

Субъективная составляющая погрешности связана с индивидуальными особенностями оператора. Как правило, эта погрешность возникает из-за ошибок в отсчете показаний и неверных навыков оператора. В основном же систематическая погрешность возникает из-за методической и инструментальной составляющих.

Методическая составляющая погрешности обусловлена несовершенством метода измерения, приемами использования средств измерения, некорректностью расчетных формул и округления результатов.

Инструментальная составляющая возникает из-за собственно погрешности средств измерения, определяемой классом его точности, влиянием средств измерения на объект измерения и ограниченной разрешающей способности средств измерения.

Целесообразность разделения систематической погрешности на методическую и инструментальную составляющие объясняется следующим:

для повышения точности измерений можно выделить лимитирующие факторы и, следовательно, принять решение либо об усовершенствовании методики, либо о выборе более точных средств измерения;

появляется возможность определить составляющую общей погрешности, увеличивающейся либо со временем, либо под влиянием внешних факторов, и, следовательно, целенаправленно осуществлять периодические поверки и аттестации;

инструментальная составляющая может быть оценена доразработки методики, а потенциальные точностные возможности выбранного метода определит только методическая составляющая.

Грубые погрешности (промахи) возникают из-за ошибочных действий оператора, неисправности средств измерения или резких изменений условий измерений. Как правило, грубые погрешности выявляются в результате статистической обработки результатов измерений при помощи специальных критериев.

3.4.3 Показатели качества измерений и испытаний

Единство измерений, однако, не может быть обеспечено только знанием погрешностей. При проведении измерений также важно знать показатели качества измерений. Под качеством измерений понимают совокупность свойств, обусловливающих получение результатов с требуемыми точностными характеристиками в необходимом виде и в установленные сроки.

Качество измерений характеризуется такими показателями, как точность, правильность и достоверность. Эти показатели должны определяться по оценкам, к которым предъявляются требования состоятельности, несмещенности и эффективности. Причем, в отличие от числовых характеристик, оценки являются случайными величинами, значение которых зависит от числа наблюдений n.

Состоятельной называют оценку, которая при n→ ∞ сводится по вероятности к оцениваемой величине.

Несмещенной называется оценка, математическое ожидание которой равно оцениваемой величине.

Эффективной называют такую оценку, которая имеет наименьшую дисперсию σ² = min.

Точность измерений определяется близостью к нулю погрешности результата измерения. Количественно точность может быть выражена обратной величиной модуля относительной погрешности, определенной в долях.

Правильность измерений определяется близостью к нулю систематической погрешности, т.е. результат «исправлен» на величину систематической погрешности.

Достоверность измерений определяется степенью доверия к результату и характеризуется вероятностью того, что истинное значение измеряемой величины лежит в указанных окрестностях действительного. Эти вероятности называют доверительными, а окрестности – доверительным интервалом с доверительными границами.

Доверительным интервалом от – Δ_д до + Δ_д называют интервал значений случайной погрешности, который с заданной доверительной вероятностью Р_д накрывает истинное значение измеряемой величины:

Р_д {`X - Δ<sub>д</sub> ≤ Х ≤ `X + Δ_д }.

При малом числе измерений (n 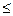20…25) и использовании нормального закона не представляется возможным определить доверительный интервал, так как нормальный закон распределения описывает поведение случайной погрешности в принципе при бесконечно большом числе измерений.

Поэтому при малом числе измерений используют распределение Стьюдента (предложенное английским статистиком Госсетом, публиковавшимся под псевдонимом «студент»), которое обеспечивает возможность определения доверительных интервалов при ограниченном числе измерений.

Границы доверительного интервала при этом определяются по формуле

Δ_д = t·S( ),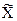

где t – коэффициент распределения Стьюдента, зависящий от задаваемой доверительной вероятности Р_д и числа измерений n.

При увеличении числа наблюдений n распределение Стьюдента быстро приближается к нормальному распределению и совпадает с ним уже при n ≥30.

Следует отметить, что результаты измерений, не обладающие достоверностью, т. е. степенью уверенности в их правильности, не представляют ценности. К примеру, датчик измерительной схемы может иметь весьма высокие метрологические характеристики, но влияние погрешностей от его установки, внешних условий, методов регистрации и обработки сигналов приведет к большой конечной погрешности измерений.

При проведении испытаний их качество, наряду с такими показателями, как точность, правильность и достоверность, характеризуется также сходимостью и воспроизводимостью результатов.

Очевидно, что два испытания одного и того же объекта одинаковым методом не дают идентичных результатов. Объективной мерой их могут служить статистически обоснованные оценки ожидаемой близости результатов двух или более испытаний, полученных при строгом соблюдении их методики. В качестве таких статистических оценок согласованности результатов испы­таний и принимаются сходимость и воспроизводимость.

Сходимость – это близость результатов двух испытаний, полученных одним методом, на идентичных установках, в одной лаборатории. Воспроизводимость отличается от сходимости тем, что оба результата должны быть получены в разных лабораториях.