Получение и представление результатов измерений

3.5.1. Постановка измерительного эксперимента

При постановке измерительного эксперимента прежде всего требуется определить, какие по числу измерений (однократные или многократные) измерения следует осуществлять для определения значения измеряемой физической величины. Общим здесь является следующий подход:

если систематическая погрешность является определяющей, т.е. ее значение существенно больше значения случайной погрешности, то целесообразно использовать однократные измерения для получения значения измеряемой величины;

если случайная погрешность является определяющей, то необходимо использовать многократные измерения.

Необходимо учитывать то, что систематическая погрешность вызывает смещение результатов измерений и является наиболее опасной тогда, когда о существовании ее не подозревают. Обнаружение систематической погрешности измерений является одной из наиболее сложных задач метрологии. В том или ином виде ее всегда приходится решать при подготовке к измерениям.

3.5.2 Обработка результатов эксперимента

В настоящее время для обработки экспериментальных данных прямых многократных измерений принято использовать методы математической статистики. При этом следует помнить, что применение этих методов позволяет получить корректные результаты только в том случае, когда из экспериментальных данных исключены систематические погрешности.

Обработка экспериментальных данных прямых многократных измерений в общем случае предусматривает выявление закономерности поведения случайной погрешности (определения закона распределения) и статистические процедуры исключения грубых погрешностей.

Нормальный закон распределения является наиболее распространенным законом распределения случайных величин, в том числе и случайных погрешностей. Поэтому в практике обработки экспериментальных данных, когда число измерений мало (не превышает 5…25), пользуются вполне оправданным предположением, что закон распределения случайной погрешности является нормальным, а грубые погрешности не выявляются или определяются и отбрасываются интуитивно.

Методы математической статистики предполагают определение вместо характеристик нормального распределения их оценок. Так, вместо математического ожидания М[Х], т.е. значения величины, вокруг которого группируются результаты отдельных измерений при бесконечном числе измерений, определяют его оценку, которая представляет собой среднее арифметическое `Х при конечном числе измерений:

М[Х] ≈ `Х = 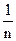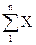_i ,

где X_i – результат i –го измерения, n – число измерений.

Вместо среднеквадратического отклонения σ, характеризующего рассеяние результатов отдельных измерений относительно математического ожидания, определяют оценку среднеквадратического отклонения результата измерений по формуле

S(`Х )=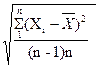

Также при обработке экспериментальных данных прямых многократных измерений принято вычислять интервальную оценку погрешности, которая определяется с использованием точечной погрешности S(`Х ) и доверительных интервалов.

Для обеспечения единства технических измерений задаются значением доверительной вероятности Р_д = 0,95 и определяют значение доверительного интервала. Коэффициент t обычно определяют по таблице вместо того чтобы рассчитывать по сложной формуле, описывающей распределение Стьюдента.

Последовательность обработки экспериментальных данных прямых многократных измерений приведена ниже. При этом предполагается:

результаты измерений являются исправленными, т.е. из них исключена известная систематическая погрешность;

неисключенные систематические погрешности настолько малы, что ими можно пренебречь;

результаты измерений являются равнорассеянными величинами (такие результаты получаются при выполнении измерений одним оператором с помощью одних и тех же средств измерений);

из результатов измерений исключены грубые погрешности (промахи);

число измерений не превосходит 15…25 (в этом случае признается и не проверяется нормальность распределения случайных погрешностей).

Алгоритм обработки экспериментальных данных прямых многократных измерений:

1. Получение n результатов наблюдений.

2. Вычисление среднего арифметического`Х.

3. Вычисление оценки среднеквадратического отклонения результата измерения S(`Х ).

4. Принятие значения доверительной вероятности Р_д (для технических измерений Р_д = 0,95).

5. Определение коэффициента t в зависимости от Р_д и n по таблице распределения Стьюдента.

6. Определение доверительных границ Δ_д случайной погрешности.

7. Запись результата измерений с использованием правил округления в виде А =`Х ± Δ_д с обязательным указанием (Р_д = ; n = ).

Обработка экспериментальных данных прямых однократных измерений.

Результаты однократных измерений также являются случайными величины, но из-за незнания закона распределения не могут быть подвергнуты статистической обработке. Поэтому результат прямого однократного измерения записывают в виде интервальной оценки:

Α = X ± Δ,

где X – значение физической величины, найденное по шкале измерительного средства; Δ – абсолютная погрешность для найденного значения X, определяемая по технической документации на средство измерения.

Для избежания получения промахов при однократных измерениях допускается проведение 2 - 3 замеров с нахождением среднего арифметического результата измерения, но без последующей статистической обработки.

3.5.3 Представление результатов измерений

Практикой обработки результатов измерительных экспериментов выработаны правила округления результатов, которые по соглашению признаются и применяются при выполнении любых, в том числе технических, измерений.

Погрешность результата измерения физической величины должна давать представление о том, какие цифры в его числовом значении являются сомнительными. Поэтому числовое значение результата измерения должно быть представлено так, чтобы оно оканчивалось десятичным знаком того же разряда, что и значение его погрешности. Большее число разрядов не имеет смысла, так как не уменьшаетнеопределенности результата, а меньшее, которое может быть получено путем округления, увеличивает неопределенность результата.

Поэтому погрешность результатов технических измерений нецелесообразно выражать большим числом цифр. Достаточно ограничиться одной-двумя значащими цифрами. Причем две цифры используются только при записи погрешности ответственных, точных измерений.

Для округления и записи результатов измерений используются следующие правила.

1. Результат измерения оканчивается цифрой того же разряда, что и значение его погрешности, при этом в десятичной дроби нули числового значения результата отбрасываются только до разряда, который соответствует разряду числового значения погрешности.

2. Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяются. При этом лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются.

3. Если цифра старшего из отбрасываемых разрядов больше или равна 5, а за ней следуют отличные от нуля цифры, то последняя оставляемая цифра увеличивается на единицу.

4. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она нечетная.

При использовании приведенных правил число значащих цифр в числовом значении результата измерения позволяет ориентировочно судить о точности измерения.