Найдем проекцию вектора скорости на касательную
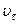 =
= 
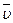

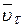 - проекция вектора скорости на касательную
- проекция вектора скорости на касательную
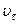 =
= 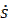

 =
= 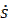
Опять возвращаемся к математике.
Положительное направление оси можно определить единичным вектором.
Запишем проекцию любого вектора на любую ось:
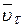 =
= 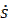
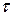 cos (
cos ( 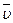
 )
)
cos 0 = 1
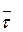 2 = 12 = 1
2 = 12 = 1
окончательно
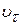 =
= 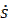 (7)
(7)
Сравним формулы (3) и (4). Эти величины могут отличаться знаком. Договоримся обозначать 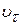 через
через 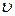
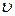 =
= 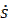 (8)
(8)
Скорость, определенная формулой (6) называется алгебраической скоростью точки, а знак может быть больше, меньше или равна нулю.
Если
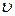 >0, то точка движется в сторону возрастания дуговой координаты
>0, то точка движется в сторону возрастания дуговой координаты
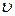 <0 то точка движется в сторону убывания дуговой координаты
<0 то точка движется в сторону убывания дуговой координаты
Эти величины могут отличаться только знаком, алгебраическое значение у них одинаковое.
Договоримся и модуль скорости, и его проекцию обозначать буквой 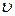 .
.
Окончательно:
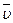 =
= 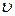

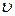 =
= 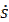
Пример
Пусть
s = 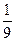 t 2 -
t 2 - 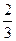 t
t
Определить направление движения точки
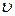 =
= 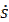 =
= 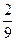 t -
t - 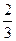 =
= 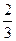 (
( 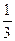 t -1)
t -1)
Знакскоростиопределяетсязнакомскобки:
если 0 < t < 3, то скорость 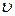 <0 ,
<0 ,
при t = 3 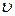 =0, т.е. в данный момент точка остановилась,
=0, т.е. в данный момент точка остановилась,
если t > 3, то 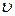 >0 , то точка движется в сторону возрастания дуговой координаты.
>0 , то точка движется в сторону возрастания дуговой координаты.
Для того, чтобы ввести понятие ускорения точки в естественной форме нам необходимы знания высшей математики.
Дата добавления: 2019-02-07; просмотров: 596;
