Б) Переходные процессы в системе ИТ-Д, замкнутой по скорости
Рассмотрим переходные процессы в системе ИТ-Д (п. 3.7) на участке, где действует отрицательная обратная связь по скорости. Если при анализе установившихся режимов мы не учитывали индуктивность цепи возбуждения, то теперь это сделать необходимо, так как момент в этой системе определяется iв, а изменение этого тока связано с Lв.
Уравнения динамики для схемы на рис. 5.21 имеют вид (примем, как и в предыдущем случае, что Мс = 0):
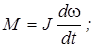 (5.27)
(5.27)
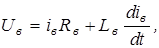 (5.28)
(5.28)
где Uв - напряжение на обмотке возбуждения;
Rв, Lв - активное сопротивление и индуктивность цепи возбуждения;
iв - текущее значение тока возбуждения.
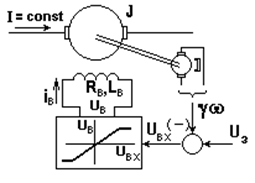
Рис. 5.21. Схема системы источник тока – двигатель, замкнутой
по скорости
Эти уравнения отражают динамические свойства системы, так как содержат члены члены с J и Lв. Кроме того, следует записать уравнения, отражающие связи между переменными.
Из общего уравнения для момента (3.1), приняв, что Ф = aiв, имеем:
М = kФI = kIaiв
или с учетом (5.27)
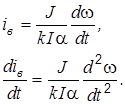
Из уравнения замыкания системы при линейном безынерционном возбудителе получаем:
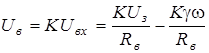
или с учетом (5.28)
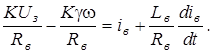
После простых преобразований получаем окончательно:
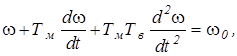 (5.29)
(5.29)
где 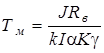 - электромеханическая постоянная времени;
- электромеханическая постоянная времени;
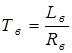 - постоянная времени цепи возбуждения;
- постоянная времени цепи возбуждения;
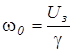 - скорость идеального холостого хода.
- скорость идеального холостого хода.
Сравнив (5.29) с (5.24), обнаруживаем полное сходство уравнений, хотя входящие в них параметры совершенно различны. В этом факте проявляется глубокая физическая общность систем на рис. 5.19 и 5.21: каждая из них имеет по два накопителя энергии и существуют условия для обмена энергией между ними.
Очевидно, что уравнению (5.29) соответствуют процессы, рассмотренные в п.а).
Дата добавления: 2019-10-16; просмотров: 1006;
