Радиус кривизны окружности равен радиусу окружности.

ρ = R

3. Определение скорости при естественном способе задания ее движения. (стр 44 –45)

Постановка задачи .

Пусть известны:

1. траектория движения точки АВ.

2. начало отсчета и положительное направление отсчета дуговой координаты s.

3. закон движения по траектории s = s(t)

Определить скорость точки по модулю и направлению.

Запишем исходную формулу, определяющую вектор скорости.

= ,

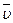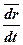Положение точки можно определить с помощью радиуса - вектора 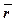, с другой стороны положение точки определяется с помощью дуговой координаты s.

Тем самым мы считаем, что радиус вектор есть функция дуговой координаты s , а она зависит от времени t , т. е. радиус - вектор есть сложная функция от времени, выраженная посредством промежуточной величины s .

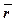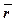= [ s(t) ],

Продифференцируем сложную функцию, для этого сначала вычислим производную по промежуточной переменной, а потом производную от промежуточной по окончательной переменной.

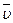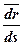
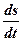= , ( 4^»)

Как известно

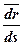= ( 4 )

т.е. если мы вернемся к формулам скорости, то можно записать

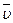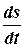
= или (5)

Вектор скорости 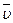направлен по касательной к траектории

Исследуем этот результат:

Если

 

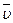> 0, то ↓↓

< 0, то ↓↑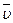

 

Определим модуль скорости, необходимо продифференцировать закон движения и взять его по модулю.

 

/ /= / /

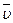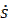
т.к. || = 1, т.е. единичный вектор, то

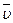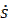/ /= / / ( 6 )