Интервалом между этими событиями называется физическая величина , квадрат которой в системе I равен

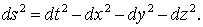
(1.11)

В соответствии с этим определением, в системе отсчета II, которая движется со скоростью V направлении оси абсцисс, квадрат интервала между теми же событиями равен

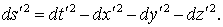
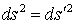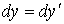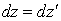Докажем, что , т.е., что численное значение интервала между двумя любыми событиями одно и то же (в системе II числено оно такое же, как в системе I). Поскольку и , то достаточно доказать усеченное равенство

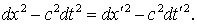
Воспользуемся преобразованиями Лоренца для дифференциалов (они не отличаются от преобразований для координат, поскольку эти последние преобразования линейные)

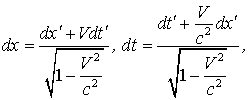
и составим разность

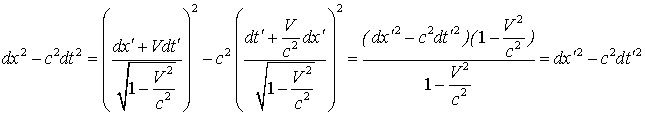
Это равенство и доказывает инвариантность интервала.

Итак, в СТО при повороте декартовых осей (и параллельном их сдвиге) инвариантами являются квадрат расстояния dx²+dy²+dz² и время dt по отдельности. Но при переходе от системы I к движущейся системе II инвариантом является квадрат интервала ds² =c²dt² -dx² -dy² -dz², тогда как значения расстояния и промежуток времени по отдельности не сохраняются. Инвариантность интервала между двумя событиями - это математическое выражение постоянства скорости света в любой системе отсчета.