Плоскость, содержащая все нормали, называется нормальной плоскостью.
Dr ( dx, dy,dz)
Тогда модуль dr будет равен:
| d 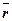 |
|  =
= 
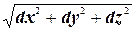 = | ds |
= | ds |
Каков смысл этого корня? Что он показывает с точки зрения геометрии?
С точки зрения геометрии | ds |- этот радикал определяет элемент дуги равный по абсолютному значению ds . Или этот радикал определяет, что криволинейную дугу s мы заменили прямолинейной ds. Это значение приближенное с точностью до величин второго порядка.(высшего порядка малости)
Тогда модуль этого вектора
/  / = /
/ = / 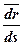 / = 1
/ = 1
Вектор 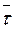 называется единичным вектором или ортом касательной к кривой АВ в точке М.
называется единичным вектором или ортом касательной к кривой АВ в точке М.
Направление 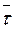
Покажем, что вектор 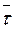 всегда направлен по касательной к траектории в сторону возрастания дуговой координаты.
всегда направлен по касательной к траектории в сторону возрастания дуговой координаты.
Сравним направления вектора d 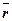 и
и 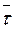
Изобразим два рисунка.
Первый рисунок.
Изображаем траекторию «а в», На этой траектории выберем точку О' начало отсчета дуговой координаты и положительное направление этой дуговой координаты.
Положение точки М на данной траектории будет определяться при помощи дуговой координаты s. Выберем близлежащую к ней точку М1.Перемещение точкиМ к М1, обозначим через d 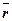 маленькая дуга ds Изобразим орт
маленькая дуга ds Изобразим орт  по касательной к траектории.
по касательной к траектории.
 |
d 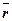 - это вектор элементарного перемещения точки за бесконечно малый промежуток времени dt.
- это вектор элементарного перемещения точки за бесконечно малый промежуток времени dt.
Он всегда направлен по касательной в сторону движения точки и абсолютно не важно в каком направлении точка движется.( в сторону увеличения или убывания дуговой координаты).
Записи будем делать под одной и другой картинкой
| При движении в положительном направлении, когда дуговая координата s возрастает. ( ds > 0 ) | При движении в отрицательном направлении, когда дуговая координата s убывает. ( ds < 0 ) |
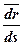 ↓↓ d ↓↓ d 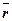 или
или
 ↓↓ d ↓↓ d 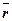
| 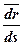 ↓↑ d ↓↑ d 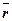 или
или
 ↓↑ d ↓↑ d 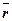
|
Второй рисунок.
 Изображаем траекторию «а в», На этой траектории выберем точку О' начало отсчета дуговой координаты и положительное направление этой дуговой координаты.
Изображаем траекторию «а в», На этой траектории выберем точку О' начало отсчета дуговой координаты и положительное направление этой дуговой координаты.
Положение точки М на данной траектории будет определяться при помощи дуговой координаты s. Выберем близлежащую к ней точку М1,но изобразим ее в противоположном направлении. Перемещение точкиМ к М1, обозначим через d 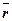 маленькая дуга ds. Изобразим орт
маленькая дуга ds. Изобразим орт  по касательной к траектории.В этом случаеds < 0.
по касательной к траектории.В этом случаеds < 0.
Вывод
Вектор 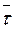 - всегда направлен по касательной к траектории в сторону возрастания дуговой координаты s.
- всегда направлен по касательной к траектории в сторону возрастания дуговой координаты s.
Рассмотрим некоторую пространственную линию. На этой линии возьмем две близкие друг к другу точки М и М1 и построим в этих точках орты касательных  и
и 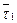 .
.
По модулю они одинаковые, но у нас кривая линия, поэтому направлены они будут по разному.
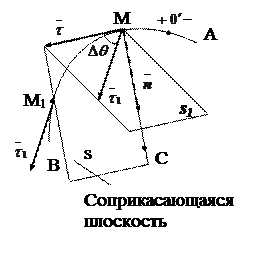 |
Вектор 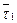 перенесем параллельно самому себе в точкуМ .
перенесем параллельно самому себе в точкуМ .
Произведем следующее построение: через  и
и 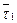 проведем плоскость s1
проведем плоскость s1
Вектор  при этом будет менять свою ориентацию в пространстве.
при этом будет менять свою ориентацию в пространстве.
Плоскость s1 будет как-то поворачиваться вокруг вектора  .Пока не займет некоторое предельное положение.
.Пока не займет некоторое предельное положение.
При М → М1 вдоль АВ плоскость будет поворачиваться вокруг вектора  пока не займет предельное положение плоскости s1 .
пока не займет предельное положение плоскости s1 .
Изобразим эту плоскость красным мелом.
Плоскость S называется соприкасающейся плоскостью в точке М к АВ.
Любой перпендикуляр к касательной называется нормалью.
Плоскость, содержащая все нормали, называется нормальной плоскостью.
Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью, нормаль лежащая в перпендикулярной плоскости называется – бинормалью.
Необходимо изобразить еще два единичных вектора: главную нормаль и бинормаль.
Вводим единичный вектор :
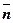 - орт главной нормали (всегда будем направлять его в сторону вогнутости траектории.)
- орт главной нормали (всегда будем направлять его в сторону вогнутости траектории.)
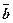 - орт бинормали, его направление будем определять следующей формулой:
- орт бинормали, его направление будем определять следующей формулой:
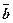 =
= 
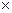
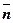
т.о  ,
, 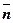 ,
, 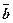 - правая тройка векторов.
- правая тройка векторов.
Так как мы привыкли пользоваться правой системой координат, то направим вектор бинормали так, чтобы данные вектора образовали правую тройку векторов.
Плоскость проходящая через орты 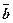 и
и 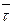 называется спрямляющей плоскостью к траектории АВ в точке М.
называется спрямляющей плоскостью к траектории АВ в точке М.
Совокупность плоскостей соприкасающейся, нормальной и спрямляющей представляют собой трехгранник с вершиной в точке М. Он называется естественным трехгранником.
Сделаем еще один рисунок.
Изобразим траекторию движения точки АВ. Выбираем точку М на траектории. Изобразим 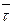 - орт касательной,
- орт касательной, 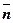 - орт главной нормали,
- орт главной нормали, 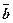 -орт бинормали.
-орт бинормали.
Изображаем соприкасающеюся плоскость, проходящую через 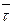 - орт касательной,
- орт касательной, 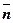 - орт главной нормали.
- орт главной нормали.
Затем нормальную плоскость проходящую через 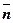 - орт главной нормали,
- орт главной нормали, 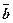 -орт бинормали.
-орт бинормали.
Через орты 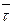 - орт касательной и
- орт касательной и 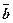 -орт бинормали проводим спрямляющую плоскость.
-орт бинормали проводим спрямляющую плоскость.
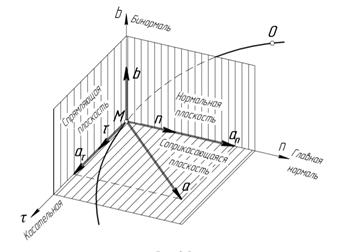
Оси совпадающие по направлению с ортами  ,
, 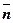 ,
, 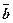 называются естественными осями координат, а их совокупность естественной системой координат.
называются естественными осями координат, а их совокупность естественной системой координат.
Система меняет свою ориентацию в пространстве, поэтому он еще называется подвижным трехгранником.
2. Кривизна линии. (стр 38 –40)
Мы с вами уже знаем, что прямая – это линия нулевой кривизны, окружность – это линия постоянной кривизны.
Нам необходимо ввести величину, которая характеризовала бы искривленность произвольной линии в любой ее точке.
Введем угол между векторами  и
и 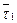 и обозначим
и обозначим 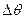 (тетта).
(тетта).
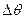 - называется углом смежности, соответствующий дуге М М1.
- называется углом смежности, соответствующий дуге М М1.
Этот угол характеризует поворот орта касательной при переходе от М к М1 , вследствие искривления дуги на участке М М1.
Обозначим приращение дуговой координаты s при переходе от точки М к М1 через 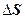 .
.
М М1 = 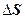
Введем понятие средней кривизны:
Кср = | 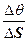 |
|
Эта величина показывает, на сколько повернется орт касательной при единичной дуге и характеризует искривленность дуги ММ1.
Если бы дуга была бы одинакова изогнута, то очевидно эта величина бы характеризовала одинаковую искривленность по всем точкам этого участка. Но у нас по всем точкам дуга искривлена по - разному.
Поэтому, чем меньше 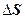 и чем ближе М1 к М тем меньше искривление линии.
и чем ближе М1 к М тем меньше искривление линии.
Нам необходимо определить искривленность в каждой точке.
Для того, чтобы узнать кривизну в точке М следует устремить точку М к М1 .
Совершим предельный переход( 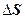 →0 )
→0 )
К = 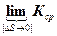 =
= 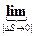 |
| 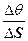 | (2)
| (2)
Величина, равная пределу средней кривизны при 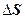 →0 , называется кривизной линии в данной точке.
→0 , называется кривизной линии в данной точке.
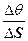 - данная величина не является дифференциалом, не будет производной. Обе величины бесконечно малые.
- данная величина не является дифференциалом, не будет производной. Обе величины бесконечно малые.
Вводим понятие радиуса кривизны:
 ρ =
ρ = 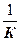 ( 3 )
( 3 )
Дата добавления: 2019-02-07; просмотров: 648;
