Метод деформируемого многогранника Нелдера, Мида

Методы поиска или методы минимизации без ограничений, не использующие производные

В методах поиска направления минимизации определяются на основании последовательных вычислений целевой функции .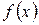

Метод прямого поиска

Простейший метод прямого поиска заключается в том, что последовательно осуществляется одномерный поиск по каждой переменной, тогда как другие переменные остаются постоянными. Во многих случаях этот метод работает плохо.

Метод деформируемого многогранника Нелдера, Мида

Симплекс ― это регулярный многогранник в п-мерном пространстве (в двумерном пространстве равносторонний треугольник, в трехмерном пространстве тетраэдр, то есть пирамида с четырьмя вершинами и одинаковыми ребрами, и так далее). Координаты вершин регулярного симплекса задаются с помощью матрицы

,

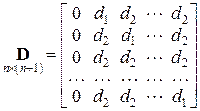столбцы которой состоят из п координат каждой из (п + 1) вершин. Здесь

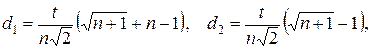
t ― расстояние между двумя вершинами (длина ребра и аналог шага h поиска).

Пусть на k-ом этапе поиска, k = 0,1,…, заданы n координат каждой из (п + 1) вершин деформируемого многогранника (вначале это регулярный симплекс) в п-мерном пространстве

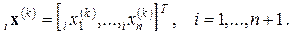
Шаг 1). Вычисляются значения целевой функции в каждой из (п + 1) вершин

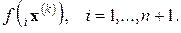
Шаг 2). Определяются вершины, в которых целевая функция принимает максимальное и минимальное значения

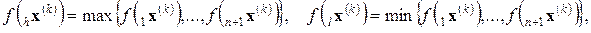
а также определяется центр тяжести всех вершин многогранника, исключая ,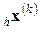

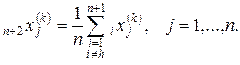
Шаг 3). Отражение: проектирование 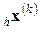через центр тяжести

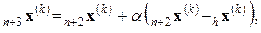
где α > 0 коэффициент отражения.

Шаг 4). Растяжение:

Если 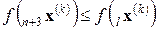, то осуществляется растяжение, то есть определяется

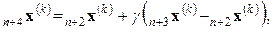
где γ > 1 коэффициент растяжения.

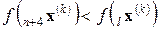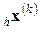Если , то заменяется на 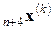и можно вернуться к шагу 1 при k = k + 1.

В противном случае 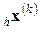заменяется на 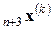и можно вернуться к шагу 1 при k = k + 1.

Шаг 5). Сжатие:

Если 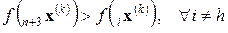, то осуществляется сжатие, то есть определяется

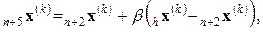
где 0 < β < 1 коэффициент сжатия. Затем 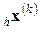заменяется на 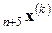и можно вернуться к шагу 1 при k = k + 1.

Шаг 6). Редукция:

Если 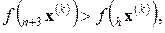то осуществляется редукция, то есть все векторы 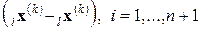уменьшаются, например, в 2 раза

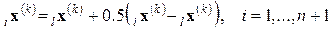
и можно вернуться к шагу 1 при k = k + 1.

Условие выхода или критерий окончания поиска

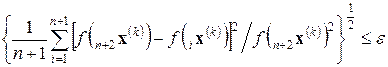, (1.2.1)

а решение задачи минимизации

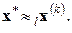(1.2.2)

Авторы рекомендовали α = 1, β = 0.5, γ = 2.

Пример 1.2.1 Решение задачи многомерной минимизации методом симплексного поиска Спендли, Хекста и Химсворта

Пусть .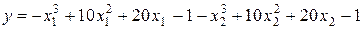

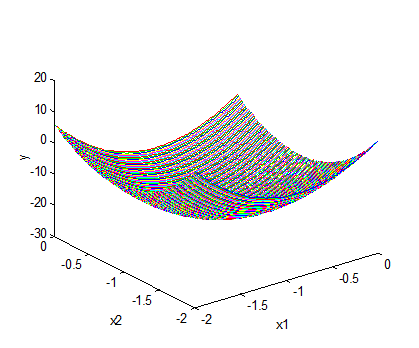
Найдем локальный минимум, ближайший к 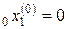, 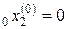методом многомерного симплексного поиска (локальный минимум, ближайший к 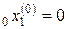, , 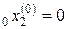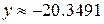при , ).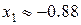

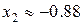Пусть t = 0.01, 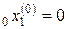, , 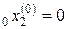, 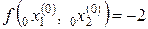п = 2.

Тогда

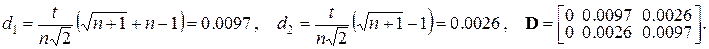
Получим 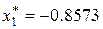, , 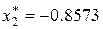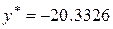при t = 0.1 после 30 шагов симплексного поиска.

М-функция:

function[xopt,fopt]=exmpl2(x01,x02,t,kmax)

n=2;

d1=t/n/sqrt(2)*(sqrt(n+1)+n-1);d2=t/n/sqrt(2)*(sqrt(n+1)-1);

d=[0 d1 d2;0 d2 d1];

for k=1:kmax

for i=1:n+1

f(i)=-d(1,i)^3+10*d(1,i)^2+20*d(1,i)^1-1-d(2,i)^3+10*d(2,i)^2+20*d(2,i)^1-1;

end

[fh,ih]=max(f);

[fl,il]=min(f) ;

disp('Центр тяжести');

xn2=zeros(1,n);

for i=1:n+1

if i~=ih

for j=1:n

xn2(j)=xn2(j)+1/n*d(j,i);

end

end

end

fn2=-xn2(1)^3+10*xn2(1)^2+20*xn2(1)^1-1-xn2(2)^3+10*xn2(2)^2+20*xn2(2)^1-1

disp('Отражение');

for j=1:n

xn3(j)=xn2(j)+(xn2(j)-d(j,ih));

end

fn3=-xn3(1)^3+10*xn3(1)^2+20*xn3(1)^1-1-xn3(2)^3+10*xn3(2)^2+20*xn3(2)^1-1

for j=1:n

d(j,ih)=xn3(j);

end

end

for j=1:n

xopt(j)=d(j,il);

end

fopt=fl;

end