Метод Гаусса (метод исключения неизвестных)
Наиболее распространенным и универсальным методом решения систем линейных уравнений является метод Гаусса, в основе которого лежит идея последовательного исключения неизвестных. Существуют различные вычислительные схемы, реализующие этот метод. Рассмотрим одну из них – схему единственного деления. Для простоты ограничимся рассмотрением системы трех уравнений с тремя неизвестными:
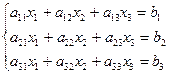 (4.4)
(4.4)
Пусть 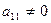 . Разделив первое уравнение системы (4.4 ) на
. Разделив первое уравнение системы (4.4 ) на 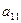 , получим:
, получим:
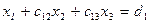 , (4.5)
, (4.5)
где 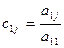 ,
, 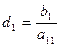 .
.
Пользуясь уравнением (4.5), можно исключить неизвестное 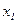 из второго и третьего уравнений системы (4.4). Для этого следует умножить уравнение (4.5) на
из второго и третьего уравнений системы (4.4). Для этого следует умножить уравнение (4.5) на 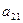 и
и 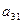 и вычесть результаты соответственно из второго и третьего уравнений системы. В результате получим:
и вычесть результаты соответственно из второго и третьего уравнений системы. В результате получим:
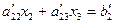
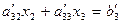 , (4.6)
, (4.6)
где 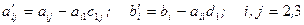 .
.
Все проделанное для системы уравнений (4.4) полностью повторяется для системы уравнений (4.6). Делим первое уравнений системы (4.6) на 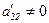 . Получаем
. Получаем
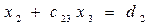 , (4.7)
, (4.7)
где 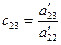 ,
, 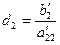 .
.
Исключив 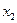 из второго уравнения системы (4.6), получаем
из второго уравнения системы (4.6), получаем
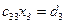 , (4.8)
, (4.8)
где 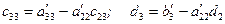
Объединяя уравнения (4.5), (4.7) и (4.8) в систему, получим:
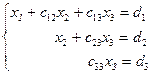 (4.9)
(4.9)
Система уравнений (4.9), представленная треугольной матрицей 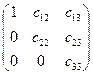 , эквивалентна исходной системе (4.4), но позволяет быстро найти все неизвестные. Начиная с третьего уравнения системы (4.9), последовательно находим:
, эквивалентна исходной системе (4.4), но позволяет быстро найти все неизвестные. Начиная с третьего уравнения системы (4.9), последовательно находим:
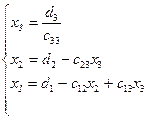 (4.10)
(4.10)
Таким образом, решение системы линейных уравнений по методу Гаусса распадается на два этапа:
u прямой ход – приведение системы уравнений (4.4) к виду (4.9) с треугольной матрицей;
u обратный ход = определение неизвестных по формуле (4.10).
Рассмотрим общий случай, а именно решение системы линейных уравнений вида:
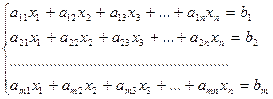 ,
,
Которая в матричной форме имеет вид: 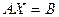 , где А – матрица размера
, где А – матрица размера 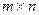 имеет компоненты
имеет компоненты 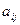 , а матрицы-столбцы X и B соответственно компоненты
, а матрицы-столбцы X и B соответственно компоненты 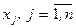 и
и 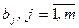
Элементарными преобразованиями приведём расширенную матрицу 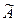 этой системы к ступенчатому виду. При этом возможны три случая:
этой системы к ступенчатому виду. При этом возможны три случая:
1) система получилась в виде: 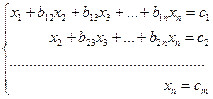 .
.
Начиная с последней строки, двигаясь к первой, находим последовательно 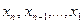 . Решение системы будет единственное. Этот случай соответствует
. Решение системы будет единственное. Этот случай соответствует 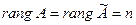 .
.
2) система получилась в виде: 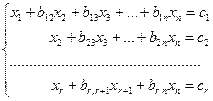 .
.
Неизвестные 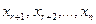 переносим в правую часть и считаем их свободными
переносим в правую часть и считаем их свободными 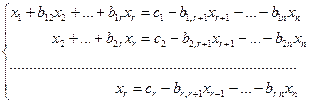
Далее, начиная с последней строки, находим неизвестные 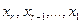 , выраженные через свободные неизвестные
, выраженные через свободные неизвестные 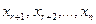 .
.
Решений системы бесчисленное множество. Этот случай соответствует 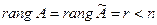 .
.
3) Система получилась в виде: 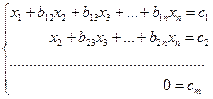 ,
, 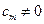 - система не совместна. Этот случай соответствует
- система не совместна. Этот случай соответствует 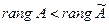 .
.
Пример 4.3.Установить совместность и решить систему: 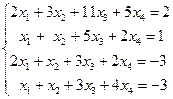 .
.
Решение:
В расширенной матрице системы поменяем 1-ю и 2-ю строки для того, чтобы элемент 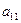 был равен «1».
был равен «1».
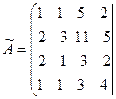
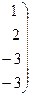 ~
~ 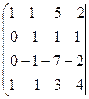
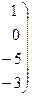 ~
~ 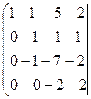
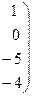 ~
~ 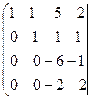
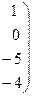 ~
~
~ 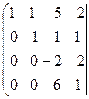
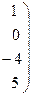 ~
~ 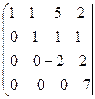
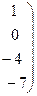 ~
~ 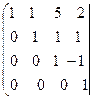
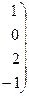
Имеем 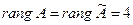 . Ранги матрицы системы и её расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение её единственно. Запишем преобразованную расширенную матрицу в виде системы уравнений:
. Ранги матрицы системы и её расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение её единственно. Запишем преобразованную расширенную матрицу в виде системы уравнений:
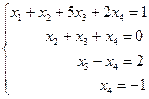 , следовательно
, следовательно 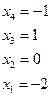 .
.
Ответ запишем в виде 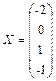 .
.
Дата добавления: 2019-02-07; просмотров: 421;
