Линейные электрические цепи постоянного тока.

Задачи анализа и расчета электрических цепей. Положительные направления напряжения, ЭДС и тока. Источниками электрической энергии являются устройства, в которых различные виды энергии превращаются в электрическую. Важнейшей характеристикой источника служит электродвижущая сила (ЭДС). ЭДС является причиной возникновения напряжения U и тока I в электрической цепи. Одной из задач анализа и расчета электрической цепи является определение токов, напряжений и мощностей на различных ее участках. Для этого необходимо знать ЭДС и сопротивления источников и приемников. В некоторых случаях ЭДС с внутренним сопротивлением может отсутствовать в электрической цепи в явном виде. Вместо этого указывается напряжение, подводимое к электрической цепи от источника, а последний только подразумевается.

При расчете цепи кроме известных направлений величин задаются еще произвольные направления для искомых величин, которые считают положительными

( Е>0, U>0 и I>0).

Электрическая цепь. Основные понятия. Электрическая цепь -это совокупность источников, потребителей и связывающихихустройств. Простейшая цепь представлена на рис. 1.1.

При описании сложной электрической цепи (рис. 1.2) используются понятия: узел, ветвь, контур.

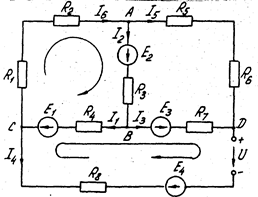
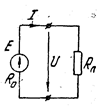
Рис 1.1 Рис 1.2

Узел - это точка, в которой сходятся не менее трех ветвей (точки А, В, С, D).

Ветвь - это часть цепи, где все элементы соединены последовательно, а токи в них всегда одинаковы (ветви АС, СВ. АВ и т.д.). Контур - это замкнутая в геометрическом смысле часть цепи (контур АВСА).

Основные законы электрических цепей. Согласно закону Ома, ток в замкнутой неразветвленной цепи (см. рис. 1.1)

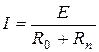(1.1)

Для участка цепи, не содержащего источника ЭДС, закон Ома имеет вид

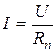(1.2)

(рис. 1.1, правая часть цепи).

Согласно первому закону Кирхгофа, сумма токов, направленных к узлу А (рис. 1.3), равна сумме токов, направленных от узла. Если токи, направленныек узлу, считать положительными, а направленные от узла - отрицательными, то, обобщая,можно сказать:

алгебраическая сумма токов, сходящихся в узле, равна нулю, т.е.

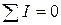(1.3)

для точки А .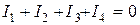

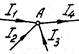Согласно второму закону Кирхгофа, во всяком замкнутом в геометрическом смысле контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура и напряжений:

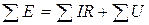(1.4) Рис 1.3

Чтобы записать второй закон Кирхгофа для конкретного контура, нужно:

1) обозначить положительные направления ЭДС, токов и напряжений; .

2) выбрать направление обхода контура;

5) составить уравнение по второму закону Кирхгофа. Со знаком плюс в соответствующую часть уравнения входят те ЭДС, токи и напряжения, положительные направления которых совпадают с направлением обхода. Так, на рис. 1.2 для контура АВСА

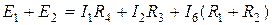
для контура СВДС

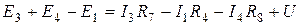
Электрическая энергия и мощность. Мощность - это интенсив­ность энергетического процесса 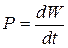. Для постоянного тока .

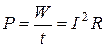Для источника (рис. 1.1)

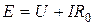
После умножения на ток I получим уравнение баланса мощ­ности цепи 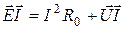. Баланс мощности - это отражение закона сохранения энергии для электрической цепи; 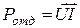- мощность, отдаваемая ис­точником во внешнюю цепь. Напряжение и ток совпадают по направ­лению. Мощность, вырабатываемая источником, 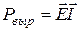. Ток совпадает по направлению с УДС.

Мощность, расходуемая на нагрев внутреннего сопротивления источника, .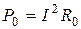

Коэффициент полезного действия:

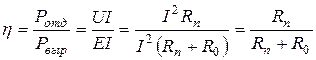
При передаче потребителям одной и той же мощности 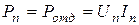ток в проводах будет тем меньше, чем больше напряжение 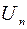установки. При этом уменьшаются потери мощности в проводах:

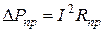, когда .

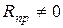Режимы работы источника электрической энергии. Характер­ными являются режимы: номинальный, холостого хода, короткого замыкания.

Номинальный режим работы - это режим, для которого рассчи­тан источник. Он характеризуется номинальным напряжением, током, мощностью. Номинальные напряжения стандартизированы: 110, 220, 440 В. Номинальные токи 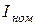, лимитируются предельно допустимыми температурами нагрева этих устройств.

Номинальная мощность 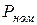. для электрического источника - это полезная мощность, отдаваемаяим во внешнюю цепь при номи­нальных условиях работы,

Режимы холостого хода и короткого замыкания являются пре­дельными режимами работы источника:

а) режим холостого хода - внешняя цепь разомкнута;

б) режим короткого замыкания - зажимы источника замкнуты проводником, сопротивление которого ничтожно мало.

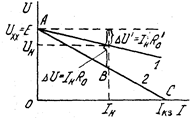Используя уравнение источника 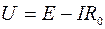, можно начертить его внешнюю характеристику 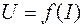(рис. 1.4). При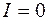 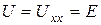(точка А), при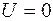 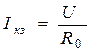(точка С).

Рис 1.4

Ток короткого замыкания 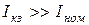и представляет опасность для источника. На рис. 1.4 вид­но, что чем больше внутреннее сопротивление источника, тем больше влияние тока на напряже­ние потребителя.

Электрические цепи с одним источником. Анализ и расчет цепей с одним источником проводит­ся с использованием законов Ома и Кирхгофа, а в более сложных случаях еще и методом эквивалентных преобразований.

Для последовательного соединения сопротивлений (рис. 1.5)

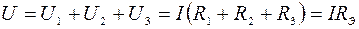, откуда

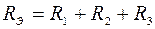
Для параллельного соединения сопротивлений (рис. 1.6)

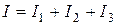или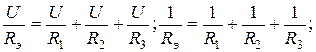

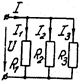
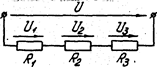
Рис 1.5 Рис 1.6

В частном случае для двух соединений .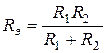

Эквивалентная проводимость 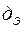для парралельного участка .

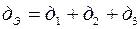Отдельно можно выделить смешанное соединение (рис. 1.7).

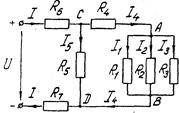
Рис 1.7

Это такое соединение, при котором на одних участках электрической цепи сопротивления соединены последовательно, а на других параллельно.

Пример. В цепи, изображенной на рис. 1.7, , , , ,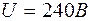

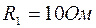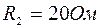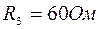Найти распределение токов в схеме.

Решение. Эквивалентное сопротивление между точками А и В

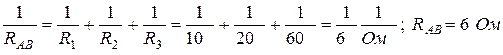
Сопротивление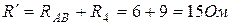

Сопротивление 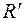параллельно сопротивлению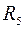

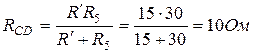
Общее сопротивление цепи

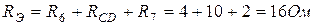
Общий ток

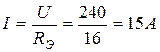
Напряжение между точками С и D

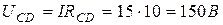
Токи в сопротивлениях 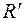и 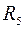определяются позакону Ома

,

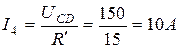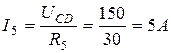
Напряжение между точками А и В

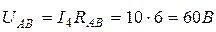
Токи в сопротивлениях 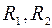и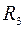

; ;

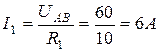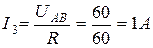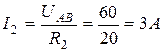
Электрические цепи с несколькими источниками, методом анализа и расчета сложных цепей является непосредственное применение первого и второго законов Кирхгофа.

Расчет сложной цепи (рис. 1.8) проводят в такой последовательности:

1) упрощают схему;

2) по первому закону Кирхгофа составляют ( 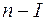) уравнений, где 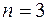- число узлов в схеме;

3) по второму закону Кирхгофа составляют не достающие уравнения т -( п -I), где

т = 5 - число ветвей схемы.

Если в результате решения токи получатся отрицательными, это значит, что действительные направления токов противоположны выбранным.

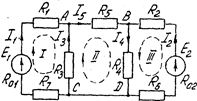Пример. Определить токи в цепи на рис. 1.8, применив законы Кирхгофа, если 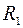= 0,3 Ом, R₂=R₆=0,4 Oм, R₃=R₄=2 Oм, R₅ =6 Oм, R₇=0,6 Oм, E₁=140В, Е₂=85В, R₀₁=0,1Ом, R₀₂=0,2Ом

Рис 1.8

Решение. На основании первого закона Кирхгофа записываем два уравнения, т.е. (n-1), где n=3:

для узла А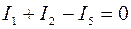

для узла В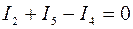

Направления обхода контуров выбираем произвольно. Число ветвей т = 5. Столько же неизвестных токов, поэтому уравнений согласно второму закону Кирхгофа три:

для контура I ;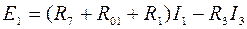

для контура II ;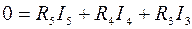

для контура III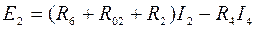

Во втором контуре нет ЭДС, и левая часть уравнения равна 0.

Решение системы с пятью неизвестными дает: 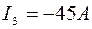(знак минус означает, что действительное направление тока противоположно принятому на схеме),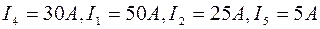

На участке DC ток 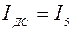и направлен от точки D и С.