Статистическая модель расчета струи. Основные расчетные соотношения

Рассмотрим изобарический участок турбулентной струи, которая в некотором начальном сечении (конец первой бочки для нерасчетных струй или срез сопла для дозвуковых и расчетных сверхзвуковых струй) имеет заданное, в общем случае неоднородное, распределение газодинамических параметров. Область, занятая струей в начальном сечении а–а, ограничена одной (для одиночных струй) или несколькими (для блочных струй) непрерывными замкнутыми кривыми.

Рис. 4.1

Для того чтобы статистически определить траектории движения всех квазичастиц, нужно задать в общем случае многомерную плотность вероятности 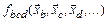, которая представляет собой совместную плотность вероятности попадания квазичастицы, начавшей свое движение из точки 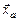начального сечения, в точки 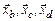и т.д. изобарического участка струи. Если ограничить задачу нахождением одноточечных вероятностных характеристик: математических ожиданий и среднеквадратических отклонений газодинамических параметров, то для этих целей достаточно знать одноточечную плотность вероятности .

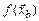Итак, требуется определить плотность вероятности 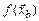, которая характеризует вероятность попадания квазичастицы из точки 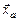начального сечения в некоторую произвольную точку 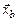изобарического участка струи. Она, как любая плотность вероятности, должна удовлетворять условиям

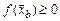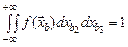; , (4.1.1)

где 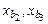– поперечные координаты точки 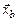; ось 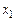начинается от сечения а–а и направлена по течению; ос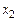и и 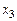образуют с осью 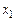правую декартову систему координат. При удалении точки 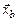от 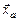плотность вероятности стремится к нулю.

Общее отклонение квазичастицы при ее случайном блуждании от прямой происходит вследствие большого количества примерно равнозначных по интенсивности актов элементарных взаимодействий. Следовательно, есть основания считать, что, в соответствии с центральной предельной теоремой теории вероятности, плотность вероятности 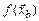описывается нормальным законом.

Если теперь сделать естественное предположение о независимости пульсаций квазичастицы по осям 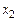и 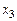, то, обобщая все вышесказанные соображения о виде функции 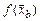, придем к следующей формуле:

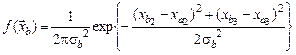, (4.1.2)

где 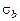– среднеквадратическое отклонение квазичастицы в сечении струи, проходящем через точку 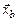; 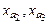– поперечные координаты точки 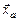. Среднеквадратическое отклонение 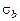, которое предполагается одинаковым по осям 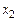и 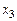, есть определяемая из опыта монотонно возрастающая функция от продольной координаты 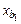точки .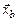

При переходе от статистических закономерностей, определяющих пульсационное движение квазичастиц, к характеристикам пульсационного поля газодинамических параметров следует рассмотреть вопрос о переносимых квазичастицами свойствах. Именно перенос квазичастицами при их случайном блуждании различных свойств обеспечивает отмеченную многими исследованиями «память» течения.

Выбор газодинамических комплексов, которые, по предположению, переносятся квазичастицами, определяется уравнениями баланса вещества, количества движения и энергии (интегральными соотношениями сохранения). Можно показать, что законы сохранения удовлетворяются, если сделать предположение о переносе каждой квазичастицей в процессе случайного блуждания значения газодинамического комплекса 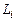в сечении а–a 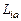c плотностью вероятности 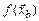в точку 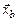. Действительно, по определению математического ожидания,

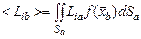, (4.1.3)

где i = 1, 2, 3; S – площадь поперечного сечения струи; индекс а обозначает параметры в начальном сечении, b – в сечении, проходящем через точку 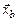. Интегрируя левую и правую части равенства (4.1.3) по сечению 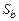, меняя порядок интегрирования в правой части и учитывая, что вероятность попадания квазичастицы в сечение 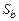– достоверное событие,

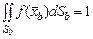, (4.1.4)

приходим к равенству

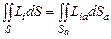, (4.1.5)

где 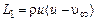, , 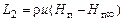, 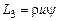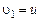– продольная составляющая скорости, S – площадь струи в произвольном поперечном сечении на изобарическом участке, 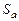– площадь начального сечения изобарического участка.

Таким образом, предположение о переносе квазичастицей комплексов 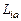позволяет автоматически (вследствие свойств плотности вероятности) удовлетворить уравнениям сохранения (3.1.1), что существенно упрощает расчетную схему и расширяет ее возможности.

Поставив каждой квазичастице в соответствие комплексы 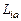, формально не будем требовать, чтобы она переносила все комплексы одновременно. Последнее замечание позволяет задавать для каждого значения i свои функции 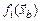, различающиеся опытными зависимостями 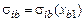. Отсюда появляется возможность получения отличных от единицы чисел Прандтля и Шмидта.

По данным экспериментальных исследований, математические ожидания комплексов L_i на больших удалениях от среза сопла распределены по сечению струи в соответствии с нормальным законом. С другой стороны, из формулы (4.1.3) следует, что на таких расстояниях

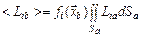, (4.1.6)

т.е. плотность вероятности имеет такой же закон изменения по сечению, как и математические ожидания комплексов 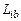. Таким образом, можно считать, что задание нормального закона для плотности вероятности 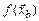и выбор свойств, переносимых квазичастицей при ее случайном блуждании, не противоречат имеющимся экспериментальным результатам и законам сохранения.

Подводя итог, запишем основные расчетные соотношения для определения первого и второго начальных моментов случайной величины 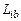на изобарическом участке турбулентной струи:

· математическое ожидание квадрата случайной величины

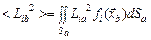; (4.1.7)

· математическое ожидание случайной величины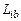

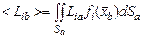; (4.1.8)

· плотность вероятности отклонения квазичастицы, переносящей комплекс 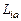, от прямой линии, проходящей через точку ,

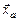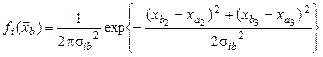, (4.1.9)

где 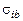– опытные зависимости.