Учет пульсаций газодинамических параметров

Пульсационные свойства случайных величин 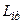в заданной точке 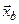будем характеризовать среднеквадратическим отклонением 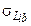, которое служит мерой величины рассеивания случайных значений комплексов 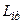относительно их математических ожиданий. Связь 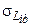с начальными моментами определяется формулой

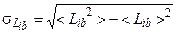, (4.6.1)

где 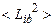– математическое ожидание квадрата случайной величины .

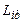В реальном процессе турбулентного смешения наблюдаемые величины среднеквадратических отклонений комплексов L_i будут меньше тех, что даются формулой (4.6.1), по двум причинам. Во-первых, пульсационные потоки перераспределяются по трем взаимно перпендикулярным направлениям, что уменьшает их в направлении оси x₁ примерно на две трети. Во-вторых, молекулярная вязкость, теплопроводность и диффузия сглаживают пульсации газодинамических параметров. В результате действительные значения среднеквадратических отклонений комплексов 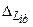связаны с величинами 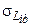соотношениями

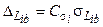, (4.6.2)

где, по опытным данным, коэффициенты 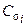можно считать постоянными по всему полю струи. В сверхзвуковых струях дополнительное уменьшение пульсаций комплексов 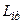вызывается демпфирующим действием пульсаций давления.

Для исследования характеристик пульсационного поля в дозвуковых и сверхзвуковых струях различных типов необходимо знать опытные константы 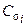, входящие в (4.6.2).

Все опытные данные свидетельствуют о том, что на интенсивность пульсаций комплексов 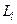основное влияние оказывает число Маха в начальном сечении изобарического участка. Статистическая обработка опытных данных приводит к таким формулам для определения математических ожиданий величин 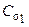в функции от значения :

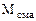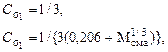
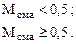(4.6.3)

Влияние других факторов на постоянную 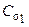не обнаружено. По крайней мере, их воздействие соизмеримо с дисперсией воспроизводимости величины 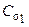по опытным данным.

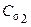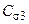Постоянные и могут быть найдены из сопоставления теоретических и экспериментальных распределений температур и концентраций примеси в дозвуковых турбулентных струях. Опыт показывает, что среднеквадратические отклонения температуры и концентрации, отнесенные к избыточным температуре и концентрации на срезе сопла, меньше среднеквадратических отклонений величины 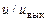примерно на 25%. Отсюда получаем соотношения для определения 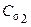и :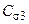

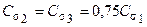, (4.6.4)

которые остаются справедливыми и для сверхзвуковых струй.

Сопоставление рассчитанных пульсационных полей с опытными показало, что предположение о постоянстве значений 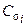является достаточно хорошим приближением к действительности. Исключение составляют лишь точки, лежащие на основном участке струи вблизи ее оси, где предположение о постоянстве значений 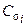приводит к завышению (примерно на одну треть) рассчитанных величин среднеквадратических отклонений по отношению к опытным. Так как зона, в которой наблюдаются отклонения результатов расчета от опыта, невелика по объему, то будем считать 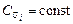по всему полю струи.

Определение статистических характеристик газодинамических параметров по известным 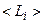и 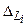требует задания ПВ для всех трех комплексов 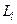, а также корреляционных связей между ними. Пусть ПВ для комплексов 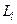описываются «обрезанным» нормальным законом

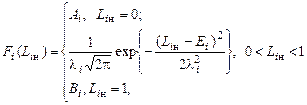, (4.6.5)

где

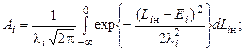(4.6.6)

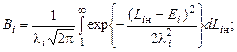(4.6.7)

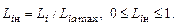(4.6.8)

Функции ПВ 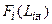являются кусочно-непрерывными: они непрерывны в открытом промежутке 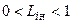и терпят разрыв в точках 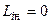и 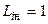. На практике, однако, удобнее пользоваться дискретным распределением случайной величины. Поэтому мы заменим функции 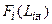их дискретными аналогами:

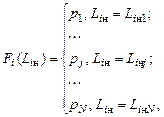(4.6.9)

где

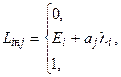
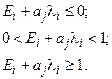(4.6.10)

Величины вероятностей 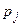и коэффициентов 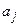были вычислены Чебышевым для различного числа членов 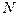в рассматриваемом дискретном распределении из условия совпадения максимального числа моментов дискретного и нормального распределений случайной величины.

Распределения вероятностей 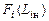для каждого нормированного комплекса 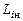содержат по две неизвестные величины: 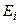и 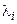. Они находятся из условия совпадения математических ожиданий 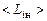и среднеквадратических отклонений 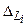нормированных комплексов 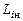для действительных и моделирующих их дискретных распределений:

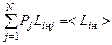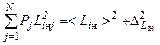; . (4.6.11)

Так как среднеквадратические отклонения случайной величины для нормального и «обрезанного» нормального законов близки друг к другу на большей части интервала изменения комплекса 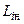, то будем считать, что

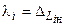. (4.6.12)

Тогда значения 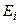могут быть найдены из первого уравнения (4.6.11) с учетом (4.6.10) и (4.6.12). Отметим, что погрешности вычислений, связанные с предположением (4.6.12), велики только в тех зонах струи, где малы значения комплексов 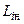, т.е. на краю струи или на очень больших удалениях от среза сопла. Обычно эти области не представляют практического интереса, и поэтому в них допускаются значительные относительные ошибки при определении статистических характеристик газодинамических параметров. Кроме того, при больших отношениях 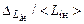, которые наблюдаются как раз при малых значениях 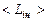, точность нахождения числовых характеристик резко падает еще по одной причине – из-за ошибок при задании ПВ газодинамических комплексов .

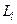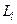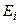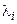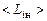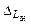Итак, мы получили дискретные плотности распределения вероятностей для нормированных комплексов в виде разложений Чебышева (см. (4.6.9), (4.6.10)). Эти плотности содержат неизвестные параметры и . Мы указали способ их определения по заданным значениям и : величины 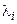мы приняли равными 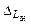, а для нахождения значений 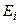записали уравнение (первое в системе (4.6.11)), которое неявным образом определяет 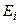при заданных величинах .

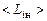Теперь мы можем выполнить заключительную операцию: определить математические ожидания и среднеквадратические отклонения газодинамических параметров.

Сделаем еще одно предположение. Будем считать, что газодинамические комплексы 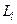статистически связаны друг с другом. Это означает, что нормированные комплексы 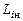могут
появляться лишь в таких сочетаниях 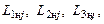когда индекс 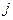одинаков для всех трех комплексов (см. (4.6.10)). Указанное предположение согласуется с имеющимися опытными данными.

Итак, пусть заданы дискретные плотности распределения случайных величин 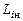в виде (4.6.9), (4.6.10). Значения 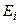и 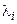считаются известными. Для каждого сочетания 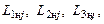где индекс 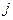пробегает значения от 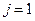до 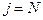, мы находим величины

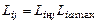. (4.6.13)

По методике, изложенной в подразд. 4.5, для каждого сочетания комплексов 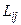находим массив газодинамических параметров .

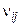Теперь мы завершаем решение поставленной в данном разделе задачи определением математических ожиданий 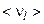и среднеквадратических отклонений 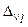случайных величин :

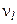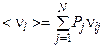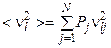; ; (4.6.14)

.

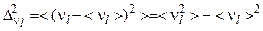В зонах струи, где 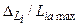велико, более точные результаты могут быть получены из градиентных соотношений типа (3.1.6).