Прочие модели турбулентности
Приведем краткий обзор моделей турбулентности, помимо изложенных в подразд. 3.1 – 3.3, с оценкой возможности их применения для расчета турбулентных изобарических струй.
Модель Колмогорова-Прандтля.Согласно этой модели турбулентная вязкость связана с кинетической энергией пульсационного движения 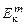 соотношением
соотношением
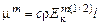 , (3.4.1)
, (3.4.1)
где 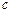 – постоянная,
– постоянная, 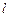 – местный масштаб турбулентности.
– местный масштаб турбулентности.
К достоинствам уравнения (3.4.1) следует отнести его согласованность с 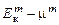 -моделью турбулентности, в которой
-моделью турбулентности, в которой 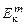 играет роль основной зависимой переменной. Более того, Ротта предложил дифференциальное уравнение для масштаба турбулентности
играет роль основной зависимой переменной. Более того, Ротта предложил дифференциальное уравнение для масштаба турбулентности 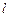 . Тем самым создаются предпосылки замыкания системы уравнений для определения осредненных газодинамических параметров в турбулентных течениях.
. Тем самым создаются предпосылки замыкания системы уравнений для определения осредненных газодинамических параметров в турбулентных течениях.
Однако, как уже указывалось ранее, 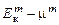 -модель сложна, содержит больше опытных постоянных, чем другие модели, ее реализация требует больших объемов вычислений. Нужные инженеру сведения дают более простые модели.
-модель сложна, содержит больше опытных постоянных, чем другие модели, ее реализация требует больших объемов вычислений. Нужные инженеру сведения дают более простые модели.
Модель Кармана.Карман предположил, что длина пути смешения 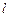 в старой теории свободной турбулентности Прандтля зависит только от двух производных:
в старой теории свободной турбулентности Прандтля зависит только от двух производных: 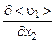 и
и 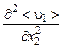 . Из них можно создать только одну комбинацию, имеющую размерность длины:
. Из них можно создать только одну комбинацию, имеющую размерность длины:
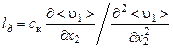 . (3.4.2)
. (3.4.2)
В результате получим выражение для турбулентного трения в виде
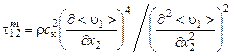 , (3.4.3)
, (3.4.3)
где 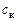 – опытная константа.
– опытная константа.
Формула (3.4.3) используется при исследовании турбулентного пограничного слоя на поверхности обтекаемого тела. Но в таком виде при расчете струй ее применить нельзя, так как в струе профиль скорости всегда имеет точку перегиба, где 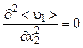 и
и 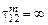 .
.
Статистические методы расчета турбулентных струйных течений. Выбранное название является в некотором смысле условным, так как все теории турбулентности, описывая поведение случайных полей газодинамических параметров, естественно, оперируют их статистическими характеристиками: математическими ожиданиями, среднеквадратическими отклонениями, характерными масштабами и т.д. Здесь же под статистическими будем понимать те модели, которые основываются на исследовании свойств и построении плотности вероятности (ПВ) распределений газодинамических параметров в поле течения и ПВ случайных блужданий турбулентных образований – квазичастиц. Иногда эти методы называются методами функции плотности вероятности. Возможно, это название является более точным.
В фундаментальных работах Хопфа выведено замкнутое уравнение, напоминающее уравнение Шредингера (линейное, первого порядка по времени), для функционала от случайного турбулентного поля. Этот функционал дает полное статистическое описание турбулентного течения. Однако математические трудности, возникающие при решении уравнения для этого функционала, таковы, что не позволили пока получить какие-либо конкретные результаты. Поэтому ограничимся упоминанием о существовании исследований подобного типа.
Более перспективно направление, основанное на использовании понятия ПВ, но уже применительно к движению некоторых турбулентных образований – квазичастиц. Идея этих моделей состоит в том, что, определив каким-либо образом вероятность попадания каждой такой квазичастицы из начального сечения изобарического участка струи в заданную точку 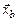 и приписав им некоторый набор свойств, которые переносятся этими квазичастицами, можно найти соответствующие моментные характеристики, например математические ожидания и среднеквадратические отклонения. Следовательно, задача сводится к нахождению вероятностных характеристик движения некоторых наборов квазичастиц. Используя теорию случайных процессов и экспериментальные данные, можно описать вероятности перехода квазичастицы из начального сечения в заданную точку
и приписав им некоторый набор свойств, которые переносятся этими квазичастицами, можно найти соответствующие моментные характеристики, например математические ожидания и среднеквадратические отклонения. Следовательно, задача сводится к нахождению вероятностных характеристик движения некоторых наборов квазичастиц. Используя теорию случайных процессов и экспериментальные данные, можно описать вероятности перехода квазичастицы из начального сечения в заданную точку 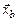 алгебраическими или дифференциальными уравнениями.
алгебраическими или дифференциальными уравнениями.
Основываясь на таком подходе, А.Г. Прудников предложил диффузионную модель для определения математических ожиданий и среднеквадратических отклонений газодинамических параметров в плоских и осесимметричных турбулентных струях с равномерным распределением параметров в начальном сечении. Модель оказалась удобной для описания математических ожиданий и дисперсий газодинамических параметров в неизотермических струях с диффузионным факелом. Она достаточно точно описывает пульсационное поле не только в зонах тангенциальных разрывов, но и в зоне диффузионного факела горения, а также вблизи оси струи.
В пользу диффузионной модели Прудникова свидетельствует и то, что она позволяет легко объяснить наблюдаемый в турбулентных изобарических струях и следах эффект последствия, в результате которого целый ряд свойств (избыточное количество движения, концентрация примеси, неизотропность и т.д.) переносятся достаточно далеко вниз по течению.
По объему получаемой информации и соответствию ее опытным данным модель Прудникова не уступает моделям типа 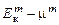 , но заметно проще и в ряде случаев позволяет получить аналитическое решение.
, но заметно проще и в ряде случаев позволяет получить аналитическое решение.
Существенным недостатком модели Прудникова явился неудачный выбор газодинамических параметров (скорость и концентрация), которые, по предположению, переносятся вместе с квазичастицами, что привело к необходимости корректировки получаемых решений для выполнения законов сохранения. Кроме того, диапазон типов турбулентных струй, которые можно рассчитывать по модели Прудникова, из-за применения указанных предположений сузился до плоских и осесимметричных турбулентных струй с однородным распределением газодинамических параметров в начальном сечении изобарического участка. В таком виде эта модель непригодна для расчета сверхзвуковых струй, истекающих на нерасчетных режимах, а также для составных струй и струй со сложной формой начального сечения изобарического участка, т.е. для тех технических приложений, которые представляют наибольший практический интерес.
В работе «Алгоритм и программа расчета параметров в турбулентных струях» (ЛМИ, 1984) указанный недостаток был исправлен. В качестве переносимых квазичастицами свойств были выбраны газодинамические комплексы 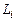 , входящие в законы сохранения (3.1.1). Это позволило распространить статистическую модель на струи со сложной формой начального сечения. В таком виде доведенная до алгоритмов статистическая модель представлена в разд. 4.
, входящие в законы сохранения (3.1.1). Это позволило распространить статистическую модель на струи со сложной формой начального сечения. В таком виде доведенная до алгоритмов статистическая модель представлена в разд. 4.
3.5. Способы осреднения газодинамических параметров
в струях с переменной плотностью
Построение уравнений Рейнольдса для сжимаемого газа поясним на примере плоской стационарной изобарической струи. Как и для несжимаемой жидкости, не будем учитывать молекулярные трение, тепловой поток и диффузию, полагая их пренебрежимо малыми по сравнению с их турбулентными аналогами.
Составим дифференциальные уравнения для математических ожиданий газодинамических комплексов:
· уравнение неразрывности
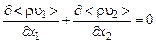 ; (3.5.1)
; (3.5.1)
· уравнение движения
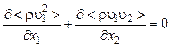 ; (3.5.2)
; (3.5.2)
· уравнение энергии
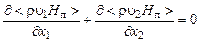 ; (3.5.3)
; (3.5.3)
· уравнение диффузии
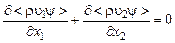 . (3.5.4)
. (3.5.4)
Приведенные в такой записи формулы описывают турбулентные струи различных типов: дозвуковые, сверхзвуковые, изотермические, неизотермические, струи с диффузионным факелом горения.
Если, следуя подходу Рейнольдса, каждый газодинамический параметр 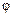 представить в виде суммы среднего значения (математического ожидания) и отклонения от среднего (пульсации):
представить в виде суммы среднего значения (математического ожидания) и отклонения от среднего (пульсации):
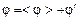 , (3.5.5)
, (3.5.5)
то, например, математическое ожидание произведения 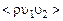 запишется в виде
запишется в виде
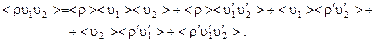 (3.5.6)
(3.5.6)
При постоянной плотности в правой части (3.5.6) отличны от нуля только первые два члена.
Большое количество корреляционных моментов, для которых, естественно, требуется подбирать на основе опыта замыкающие соотношения (при осреднении нелинейных членов 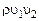 ,
, 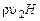 ,
, 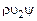 и т.д.), побудило исследователей искать более удобные формы осреднения для описания течений с переменной плотностью. Наиболее удачная форма предложена Фавром. Метод Фавра предполагает осреднение всех параметров течения, кроме давления, по плотности. Например, средние значения проекций скорости определяются по формуле
и т.д.), побудило исследователей искать более удобные формы осреднения для описания течений с переменной плотностью. Наиболее удачная форма предложена Фавром. Метод Фавра предполагает осреднение всех параметров течения, кроме давления, по плотности. Например, средние значения проекций скорости определяются по формуле
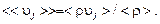 (3.5.7)
(3.5.7)
Соответственно
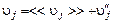 . (3.5.8)
. (3.5.8)
Для того чтобы отличить классический способ осреднения от осреднения по методу Фавра, в последнем случае средние значения будем обозначать 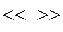 , а пульсации – двумя штрихами вверху.
, а пульсации – двумя штрихами вверху.
Применяя этот метод к слагаемым вида 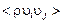 , получим
, получим
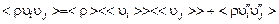 . (3.5.9)
. (3.5.9)
Сравнивая соотношения (3.5.6) и (3.5.9), убеждаемся, что метод Фавра действительно позволяет существенно уменьшить число членов в правых частях этих соотношений для турбулентных течений с переменной плотностью. Если же плотность постоянна, то классический способ осреднения и осреднение по методу Фавра совпадают.
Применение метода Фавра к системе (3.5.1) – (3.5.4) позволяет получить уравнения для осредненных газодинамических параметров в форме, аналогичной уравнениям Рейнольдса для плоской струи несжимаемой жидкости:
· уравнение неразрывности
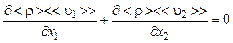 ; (3.5.10)
; (3.5.10)
· уравнение движения
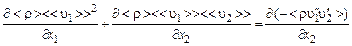 ; (3.5.11)
; (3.5.11)
· уравнение энергии
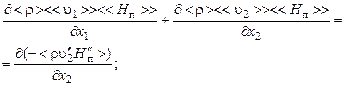 (3.5.12)
(3.5.12)
· уравнение диффузии
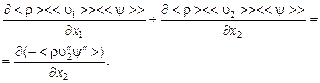 (3.5.13)
(3.5.13)
По аналогии с ламинарным течением входящие в правые части уравнений (3.5.11) – (3.5.13) выражения 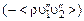 ,
, 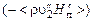 ,
, 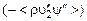 можно рассматривать соответственно в качестве компонентов тензора добавочных турбулентных вязких напряжений и турбулентных составляющих векторов теплового потока и потоков диффузии вещества струи. Продолжая и далее аналогию с ламинарным течением, можно ввести коэффициенты турбулентной вязкости
можно рассматривать соответственно в качестве компонентов тензора добавочных турбулентных вязких напряжений и турбулентных составляющих векторов теплового потока и потоков диффузии вещества струи. Продолжая и далее аналогию с ламинарным течением, можно ввести коэффициенты турбулентной вязкости 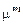 , турбулентной теплопроводности
, турбулентной теплопроводности 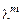 , турбулентной диффузии
, турбулентной диффузии 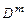 :
:
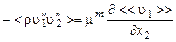 , (3.5.14)
, (3.5.14)
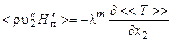 , (3.5.15)
, (3.5.15)
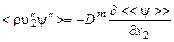 , (3.5.16)
, (3.5.16)
и турбулентные числа Прандтля 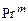 и Шмидта
и Шмидта 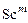
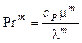 ,
, 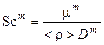 . (3.5.17)
. (3.5.17)
Система уравнений для средних значений газодинамических параметров замыкается введением дополнительных полуэмпирических гипотез, постулирующих уравнения связи характеристик турбулентного переноса с осредненными параметрами течения.
В некоторых работах используется упрощенная схема получения замкнутых систем дифференциальных уравнений для осредненного турбулентного движения: уравнения для математических ожиданий газодинамических параметров записываются формально в таком же виде, как и для ламинарного течения, а турбулентные аналоги коэффициентов вязкости, теплопроводности и диффузии определяются по эмпирическим зависимостям.
Дата добавления: 2018-11-25; просмотров: 929;
